Задание:
Варианты заданий для расчета:
| № | Параметры модели | h | n | C | m | Диапазон Т º | 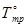
| |
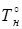
| 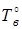
| |||||||
| A = 0,677; B = 1058 | 90% | 1.1 | 1,2 | 1,5 |
Доверительная вероятность Р * = 0,95
Вероятность безотказной работы g = 0,99
Определение класса нагревостойкости изоляции кабеля производить при ресурсе 10000 часов.
1. Модель испытания
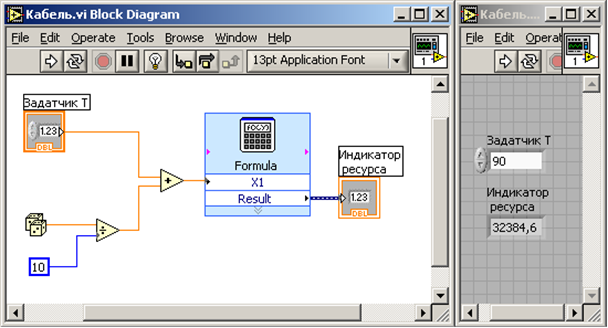
Рисунок1- Модель испытания стенда
lg(0,677)/2.306+ (1058/2.306)/(Х1) где Х1= Т –задаваемая при испытаниях температура.
2. Результаты ресурса объекта в трех точках диапазона изменения Т
| T | |||
| 15522,5 | 1256,45 | 61,965 | |
| 15485,5 | 1258,14 | 62,0015 | |
| 15374,1 | 1256,13 | 61,9738 | |
| 15402,6 | 1258,28 | 62,0145 | |
| 1256,01 | 62,0178 | ||
| 1261,3 | 62,0428 | ||
| 15545,3 | 1262,03 | 61,9719 | |
| 15460,8 | 1260,72 | 61,9566 | |
| 15461,4 | 1256,57 | 61,9751 | |
| 15509,6 | 1255,23 | 62,013 | |
| u | 4,190962 | 3,099145 | 1,792146 |
| 4,189925 | 3,099729 | 1,792402 | |
| 4,186790 | 3,099035 | 1,792208 | |
| 4,187594 | 3,099777 | 1,792493 | |
| 4,187690 | 3,098993 | 1,792516 | |
| 4,186815 | 3,100818 | 1,792691 | |
| 4,191599 | 3,101070 | 1,792195 | |
| 4,189232 | 3,100619 | 1,792088 | |
| 4,189249 | 3,099187 | 1,792217 | |
| 4,190601 | 3,098723 | 1,792483 | |
| u средн. | 4,189046 | 3,099710 | 1,792344 |
| x | 0,0(1) | 0,008(3) | 0,005 |
3.1 Вычисляем коэффициенты а1 и а2
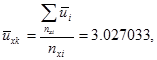
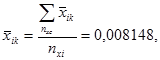
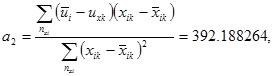
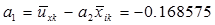
3.2 Вычисляем дисперсию для каждого испытательного режима
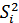
|
| 3.05207E-06 |
| 7.16035E-07 |
| 3.96513E-07 |
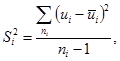
Вычисляют средневзвешенную дисперсию 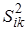 экспериментальных точек относительно средних для них значений
экспериментальных точек относительно средних для них значений 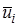 .
.
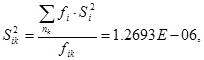 где fi – степень свободы данного режима, fi = ni – 1,
где fi – степень свободы данного режима, fi = ni – 1,
 .
.
где fik – степень свободы всех режимов.
fi=10-1=9;
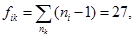
Вычисляют дисперсию 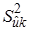 средних значений
средних значений 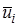 относительно соответствующих значений линии регрессии
относительно соответствующих значений линии регрессии 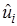 .
.
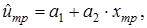 вычисляют, принимая х тр =х1,2,3
вычисляют, принимая х тр =х1,2,3
| х1 | х2 | х3 |
| 0,0(1) | 0,008(3) | 0,005 |
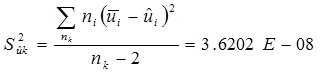
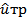
| |||
| 4,189072 | 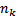 = 3 = 3
| ||
| 3,099661 | |||
| 1,792366 |
Число степеней свободы здесь f3k = nk- 2.=1
Вычисляют общую дисперсию

f 3 k = nk – 2; N – общее число образцов во всех режимах испытаний fs = N -2=28.
Вычисляют дисперсию средних значений линии регрессии (дисперсию, характеризующую возможное смещение генерального среднего относительно линии регрессии, которая вычислена по выборочным данным)
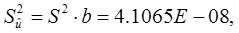
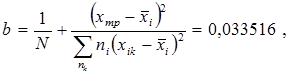
3.3 Проводят проверку гипотезы линейности.
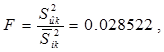 Дисперсионный критерий Фишера F является критерием оценки наличия систематических погрешностей. Критическая область для критерия Фишера соответствует Р (F > Fq) = q.
Дисперсионный критерий Фишера F является критерием оценки наличия систематических погрешностей. Критическая область для критерия Фишера соответствует Р (F > Fq) = q.
Значения Fq приведены в таблице 1.1 для уровня значимости числа серий (k = 3) k 1 = k – 1 и числа измерений (N = 30) k 2 = N – k. Если полученное значение критерия Фишера больше Fq, то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается.
| Fq(0,05) | 3,32 | |
| Fq(0,01) | 5,39 | |
| F < Fq - гипотеза принимается |
На рис. 2 изображен график зависимости среднего ресурса изоляции электрических машин и аппаратов с обмоткой из круглых проводов от температуры.
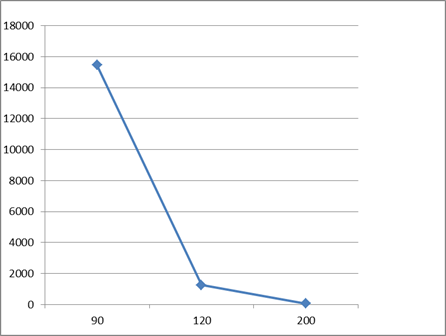
рис. 2 График зависимости среднего ресурса изоляции электрического кабеля от температуры.
4. Определяют средний ресурс при требуемой температуре 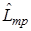 как антилогарифм
как антилогарифм 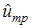
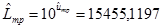 при
при 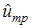 = 4,189072 и х тр = 0,0(1),
= 4,189072 и х тр = 0,0(1),
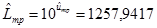 при
при 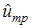 = 3,099661 и х тр = 0,008(3),
= 3,099661 и х тр = 0,008(3),
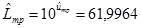 при
при 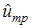 = 1,792366 и х тр = 0,005.
= 1,792366 и х тр = 0,005.
Определяют ug математическое ожидание логарифма гамма-процентного ресурса, соответствующее требуемой вероятности безотказной работы по формуле
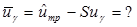
где ug =? - квантиль нормированного нормального распределения, определенный для требуемой вероятности безотказной работы (для требуемой величины g=0,99).
Определяют математическое ожидание гамма-процентного ресурса
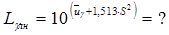
Для распределения Вейбулла.
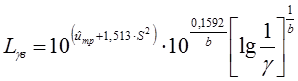
где b-? - параметр формы распределения Вейбулла, определяемый по (табл. Распределение Вейбулла) для коэффициента вариации nb, определяемого по формуле
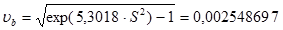
Определяют нижние доверительные границы для ресурсов.
Определяют нижнюю доверительную границу средне-логарифмических значений ресурсов при заданной доверительной вероятности Р* (или уровне значимости a=1- Р*).
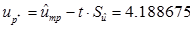
где 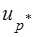 - нижняя доверительная граница средне-логарифмического ресурса при заданной доверительной вероятности;
- нижняя доверительная граница средне-логарифмического ресурса при заданной доверительной вероятности;
t = 1,96 - распределение доверительных отклонений в малой выборке (распределение Стьюдента)
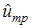 =4,189072 - значение средне-логарифмического ресурса при требуемом значении температуры
=4,189072 - значение средне-логарифмического ресурса при требуемом значении температуры
Определяем нижнюю доверительную границу среднего ресурса Lp при заданной доверительной вероятности Р=0,95
Lp=10up= 15440,99173
Определяем нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р=0,95
LPγпр=10(up+1.513S^2)= 15441,05764
Определяем нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р=0,95
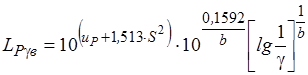
6. Определяем ресурсные характеристики кабеля при эксплуатации в условиях повышенной влажности и агрессивности среды.
В этом случае срок службы
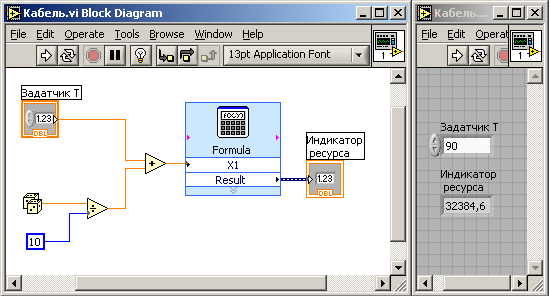
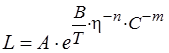 Рисунок 3- Имитационная модель объекта
Рисунок 3- Имитационная модель объекта
| T | |||
| 85305,1 | 4560,29 | ||
| 85387,2 | 4559,63 | 134,241 | |
| 85879,1 | 4552,48 | 134,175 | |
| 85439,7 | 4563,58 | 134,191 | |
| 85692,3 | 4552,86 | 134,266 | |
| 85668,3 | 4540,36 | 134,143 | |
| 86146,8 | 4554,6 | 134,262 | |
| 85693,5 | 4548,27 | 134,172 | |
| 85597,2 | 4546,04 | 133,933 | |
| 85307,1 | 4551,11 | 134,024 | |
| u | 4,930975 | 3,658992 | 2,127105 |
| 4,931393 | 3,658930 | 2,127885 | |
| 4,933887 | 3,658248 | 2,127672 | |
| 4,931660 | 3,659306 | 2,127723 | |
| 4,932942 | 3,658284 | 2,127966 | |
| 4,932820 | 3,657090 | 2,127568 | |
| 4,935239 | 3,658450 | 2,127953 | |
| 4,932948 | 3,657846 | 2,127662 | |
| 4,932460 | 3,657633 | 2,126888 | |
| 4,930985 | 3,658117 | 2,127183 | |
| u средн. | 4,932531 | 3,658290 | 2,127560 |
| x | 0,0(1) | 0,008(3) | 0,005 |
3.1 Вычисляем коэффициенты а1 и а2
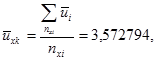
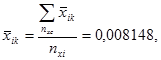

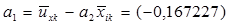
3.2 Вычисляем дисперсию для каждого испытательного режима
| Si^2 |
| 0,000001251290 |
| 0,000000025201 |
| 0,000000207089 |
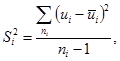
Вычисляют средневзвешенную дисперсию 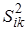 экспериментальных точек относительно средних для них значений
экспериментальных точек относительно средних для них значений 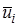 .
.
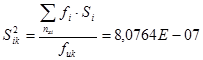
где fi = ni -1=9 (степень свободы данного режима);
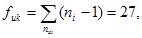
Вычисляют дисперсию 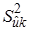 средних значений
средних значений 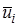 относительно соответствующих значений линии регрессии
относительно соответствующих значений линии регрессии 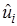 .
.
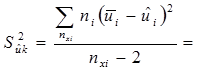
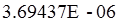
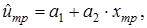 вычисляют, принимая х тр =х1,2,3
вычисляют, принимая х тр =х1,2,3
| х1 | х2 | х3 |
| 0,0(1) | 0,008(3) | 0,005 |

|
| 4,932801 |
| 3,657794 |
| 2,127786 |
Число степеней свободы здесь f3k = nk- 2.=1
Вычисляют общую дисперсию
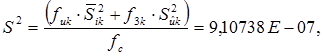
где fs = N -2=28.
Вычисляют дисперсию средних значений линии регрессии (дисперсию, характеризующую возможное смещение генерального среднего относительно линии регрессии, которая вычислена по выборочным данным)
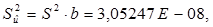
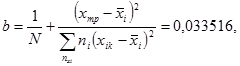
3.3 Проводят проверку гипотезы линейности.
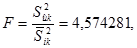
| Fq(0,05) | 3,32 | |
| Fq(0,01) | 5,39 | |
| F<Fq-гипотеза принемается |
На рис. 3 изображен графики зависимости от температуры среднего ресурса изоляции электрических машин и аппаратов с обмоткой из круглых проводов.
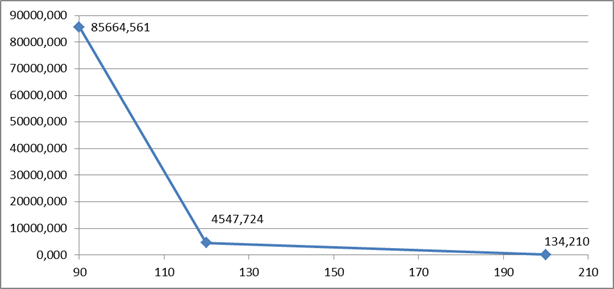
рис. 3 График зависимости от температуры среднего ресурса изоляции электрического кабеля
4. Определяют средний ресурс при требуемой температуре 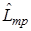 как антилогарифм
как антилогарифм 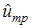
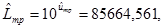 при
при 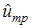 =4,932801 и х тр = 0,0(1),
=4,932801 и х тр = 0,0(1),
Определяют ug математическое ожидание логарифма гамма-процентного ресурса, соответствующее требуемой вероятности безотказной работы по формуле
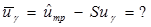
где ug =? - квантиль нормированного нормального распределения, определенная для требуемой вероятности безотказной работы (для требуемой величины g=0,99).
Определяют математическое ожидание гамма-процентного ресурса
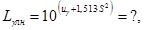
Для распределения Вейбулла.
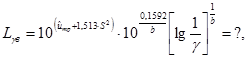
где b =? - параметр формы распределения Вейбулла, определяемый по для коэффициента вариации nb, определяемого по формуле
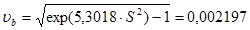
Определяют нижние доверительные границы для ресурсов.
Определяют нижнюю доверительную границу средне-логарифмических значений ресурсов при заданной доверительной вероятности Р* (или уровне значимости a=1- Р*).
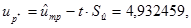
где 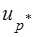 - нижняя доверительная граница средне-логарифмического ресурса при заданной доверительной вероятности;
- нижняя доверительная граница средне-логарифмического ресурса при заданной доверительной вероятности;
t = 1,96 - распределение доверительных отклонений в малой выборке (распределение Стьюдента)
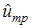 = 4,932801 - значение средне-логарифмического ресурса при требуемом значении температуры
= 4,932801 - значение средне-логарифмического ресурса при требуемом значении температуры
Определяем нижнюю доверительную границу среднего ресурса Lp призаданной доверительной вероятности Р=0,95
Lp=10up= 85597,04168
Определяем нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р=0,95
LPγпр=10(up+1.513S^2)= 85597,31326
Определяем нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р=0,95
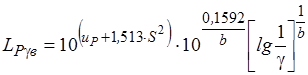 =?
=?
 2015-05-10
2015-05-10 240
240






