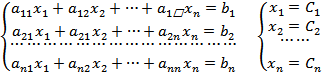
Решение системы - упорядоченный набор чисел, при подстановке которых в уравнения исходной системы получаются тождества. Система имеет решение, если 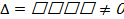
1. Метод Крамера
Вычисляется один основной и n дополнительных определителей 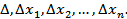
Затем находится решение:
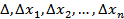
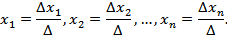
2. Метод простой итерации
Выразим из каждого уравнения одну переменную через другую.
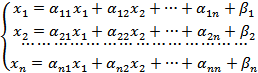
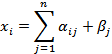
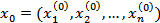
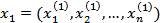
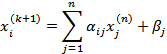
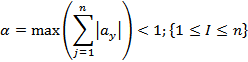
Если последовательность 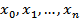 - сходящаяся, то её предел есть решение системы.
- сходящаяся, то её предел есть решение системы.
3. Метод Зейделя
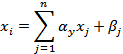
Метод состоит в том, что на каждом шаге итерационного процесса при вычислении 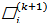 используются ранее найденные значения
используются ранее найденные значения 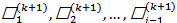 . Существует возможность преобразования системы к виду, обеспечивающему сходимость.
. Существует возможность преобразования системы к виду, обеспечивающему сходимость.
AX=B – система в матричном виде, где A – матрица коэффициентов, X – столбец переменных, B – матрица правых частей.
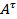 -транспонировання матрица.
-транспонировання матрица.
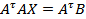
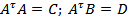
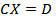 – называется нормальной системой по отношению к исходной. Такую матрицу всегда можно привести к удобному для процесса Зейделя виду.
– называется нормальной системой по отношению к исходной. Такую матрицу всегда можно привести к удобному для процесса Зейделя виду.
4. Метод Гаусса
Пусть дана линейная система (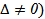
Суть метода заключается в том, что производится последовательное исключение переменных, в результате которого система приводится к треугольному виду.
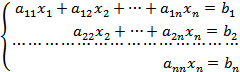
Затем из полученной системы, двигаясь снизу вверх, находят значение всех неизвестных.
Чтобы избежать накопления ошибок округления, при исключении неизвестных произвожят выбор главного элемента стоблца, т.е. элемента с наибольшим модулем коэффициента, и меняют уравнения местами так, чтобы главный элемент стал диагональным.
> 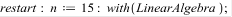
Матричный метод
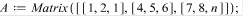

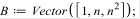

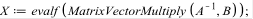

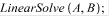
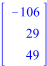
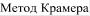
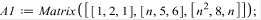
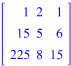
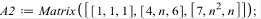
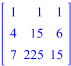
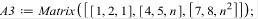
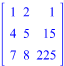
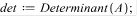







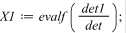

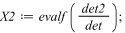

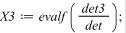

Метод Зейделя 
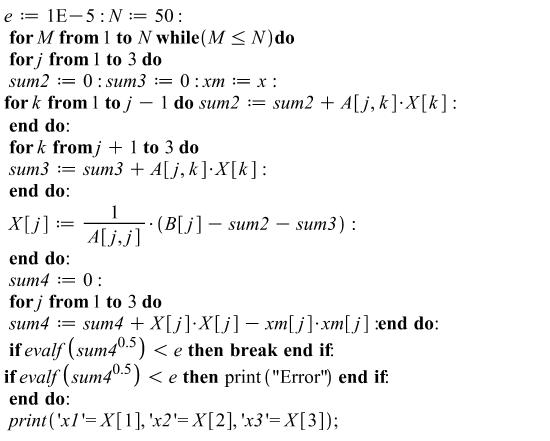
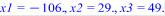
Метод Гаусса
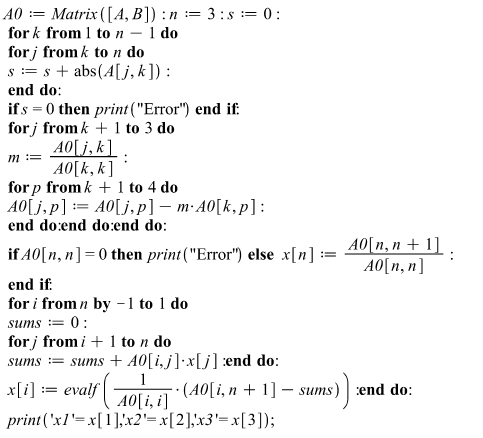
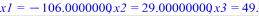
 2015-05-10
2015-05-10 351
351






