Анализ динамических режимов работы АД

Математическое описание АД в неподвижной системе координат α–β в нормальной форме Коши выглядит следующим образом:

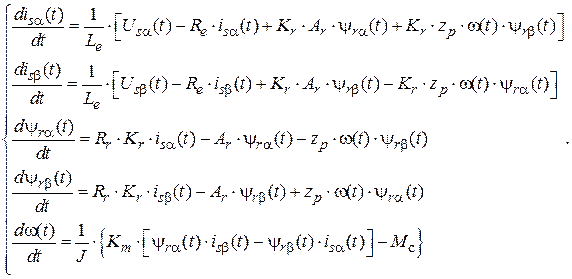
Здесь 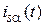, , 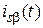, 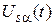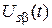– компоненты пространственных векторов тока и напряжения статора; 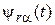, 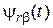– компоненты пространственного вектора потокосцепления ротора; 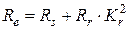, , 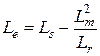, , 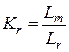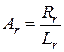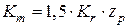– коэффициенты, учитывающие параметры АД;

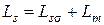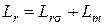, – полные индуктивности обмоток статора и ротора; 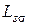, 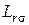– индуктивности рассеяния обмоток статора и ротора.

Определим параметры, необходимые для расчета динамики двигателя (желательно создать новый файл MathCAD!).

Индуктивность рассеяния статорной обмотки:

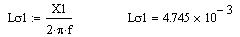
Индуктивность рассеяния роторной обмотки, приведенная к статорной:

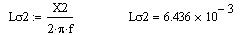
Индуктивность ветви намагничивания:

Полная индуктивность цепи статора:

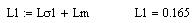
Полная индуктивность цепи ротора:

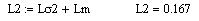
Коэффициенты для расчета динамики двигателя:

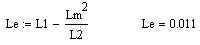
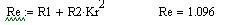
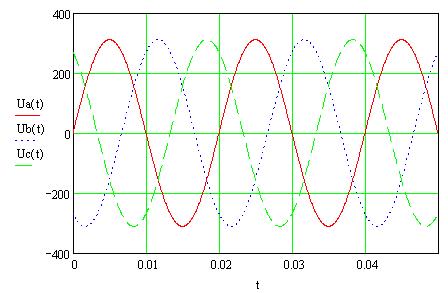
Задаем трехфазную систему статорных напряжений:

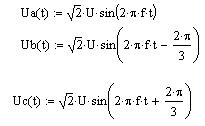
Переходим с помощью преобразования Кларка к двухфазной неподвижной системе координат:

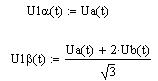
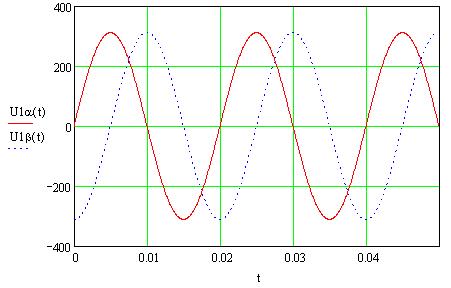
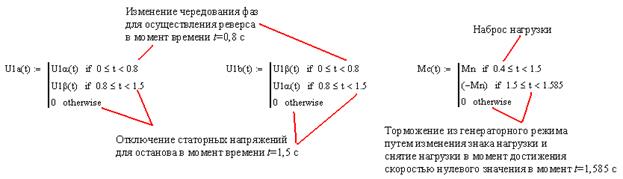
Задаем момент сопротивления АД:

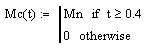
Шаг и количество точек расчета переходных процессов численным методом Эйлера:

Нулевые начальные условия:

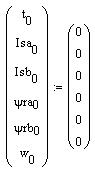
Алгоритм метода Эйлера:

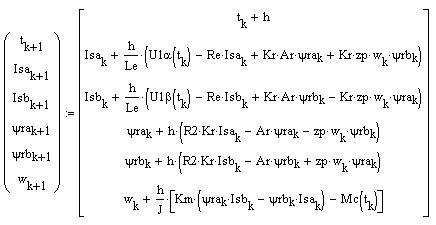
Расчетное выражение для электромагнитного момента АД:

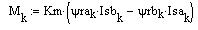
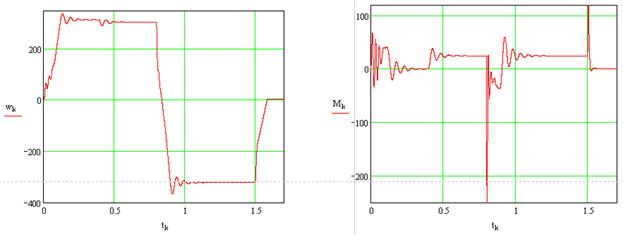
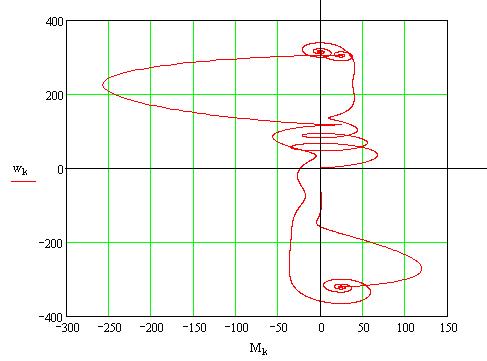
Графики переходных процессов угловой частоты вращения и момента двигателя при пуске вхолостую и набросе нагрузки:

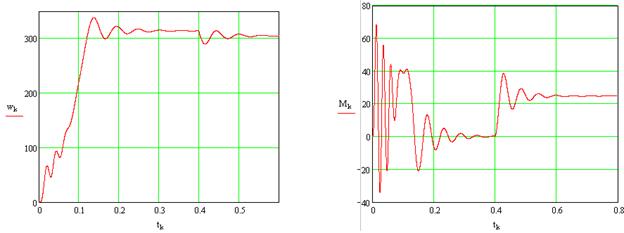
Динамическая механическая характеристика:

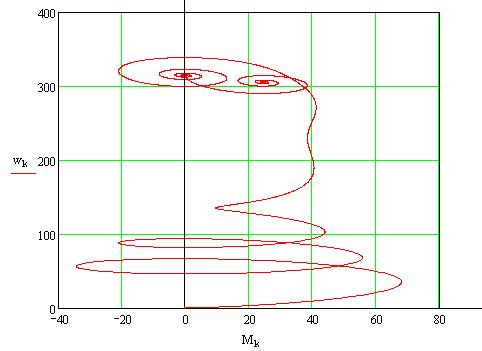
Произведем моделирование также таких режимов работы двигателя, как реверс при активном характере нагрузки и останова. Для этого введем следующие изменения в листинг MathCAD:

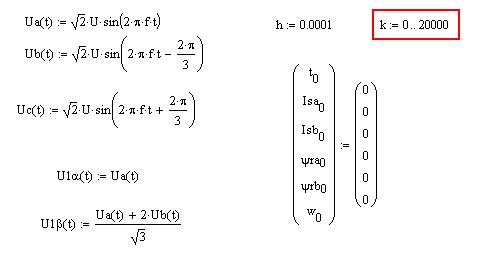
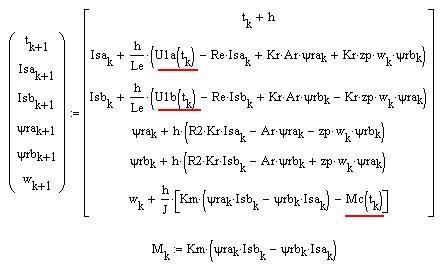
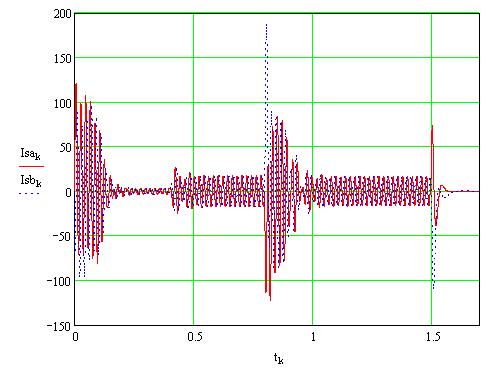
Статорные токи двигателя в двухфазной системе координат

за полный цикл работы

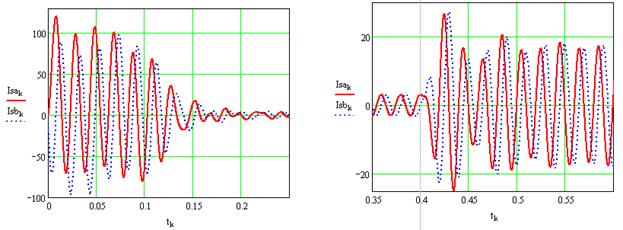
Переходные процессы изменения статорных токов АД при пуске и набросе нагрузки в увеличении

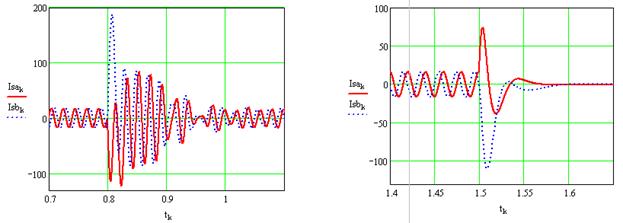
Переходные процессы изменения статорных токов АД при реверсе и останове в увеличении