Решение системы методом простой итерации

Необходимо привести заданную систему к виду, пригодному для применения метода итераций и метода Зейделя. Найти приближённое решение системы с помощью метода простой итерации. Вычисления прекратить при выполнении неравенств

().

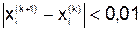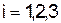Дана система:

(1) ;

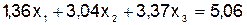(2) 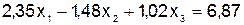;(5.5)

(3) .

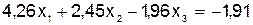Система не содержит уравнений с коэффициентами, модули которых больше суммы модулей остальных коэффициентов уравнений. Путём элементарных преобразований приводим заданную систему к такому виду:

(2)+(3) ;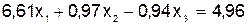

(2)-(1) 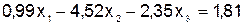; (5.6)

(3)-(1) .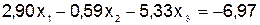

Перед каждым уравнением системы (5.6) указано, каким способом получено каждое уравнение этой системы из уравнений исходной системы (5.5).

Решим первое уравнение системы (5.6) относительно 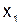, второе – относительно 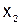, третье – относительно _:

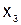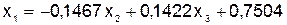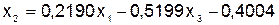; ; (5.7)

.

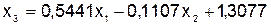Методы простой итерации и Зейделя применимы для решения системы (5.7). Находим приближённое решение системы методом простой итерации. Возьмём в качестве нулевого приближения 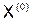столбец свободных членов:

; ; .

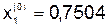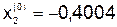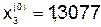Подставляя 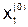, , 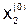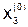в правую часть системы (5.7), получаем 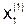, , 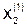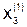и т.д. Вычисления заносим в таблицу:

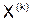
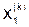
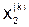
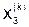
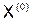
	0,7504	-0,4004	1,3077
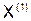
	0,9951	-0,9159	1,7378
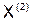
	1,0707	-1,0860	1,9505
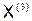
	1,1871	-1,1800	2,0105
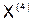
	1,2094	-1,1857	2,0842
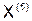
	1,2207	-1,2191	2,0970
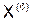
	1,2274	-1,2233	2,1068

Расчеты можно закончить, так как выполняются следующие неравенства:

;

;

.

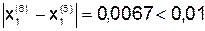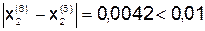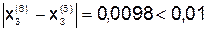Решение системы методом простой итерации таково:

;

;

.

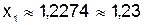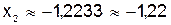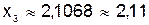Пример взят из пособия С.В. Михайленко «Прикладная математика» [4].