Методические указания по выполнению работы. Математические модели сложных динамических систем в общем случае описываются нелинейными дифференциальными уравнениями

Математические модели сложных динамических систем в общем случае описываются нелинейными дифференциальными уравнениями. Если порядок этих уравнений высокий, то при исследовании системы возникают естественные трудности. Поэтому всегда стремятся сделать модель как можно более простой.

Одним из классов моделей, допускающих их обоснованное упрощение (понижение порядка либо декомпозицию на модели меньшей размерности), является класс сингулярно возмущенных моделей.

Модель системы 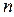-го порядка называется сингулярно возмущенной, если в пространстве 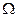параметров 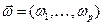системы имеется область, такая, что при параметрах, взятых из этой области, ее порядок понижается (модель, как говорят, «вырождается»). При этом в остальной части пространства параметров 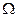порядок модели сохраняется равным 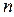, а сами значения параметров 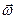близки к тем, при которых происходит вырождение (назовем их ).

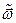При исследовании сингулярно возмущенных моделей описания динамических систем практический интерес представляет ответ на вопрос: стремятся ли процессы сингулярно возмущенной модели к процессам вырожденной модели при стремлении возмущения к нулю. Под возмущением понимается величина отличия параметров исследуемой системы от параметров, соответствующих границе области вырождения. При положительном ответе на указанный вопрос вырожденная модель может рассматриваться с некоторой допустимой точностью как модель описания процессов в системе.

В теории автоматического управления сингулярно возмущенные модели возникают довольно часто благодаря наличию в системе малых «паразитных» параметров (ими могут быть, например, малые постоянные времени, емкости, массы и т.д.), учет которых увеличивает порядок модели, или же при описании объектов с разнотемповыми процессами (примером могут служить летательные аппараты, совершающие сравнительно «быстрые» движения вокруг центра масс и «медленные» движения центра масс). Кроме того, такие модели появляются благодаря использованию больших коэффициентов усиления в цепях обратной связи в ряде методов синтеза систем управления с преднамеренным формированием разнотемповых процессов (методы больших коэффициентов, разделения движений, локализации).

В литературе наиболее исследованы сингулярно возмущенные модели с явным представлением возмущения, которые имеют вид дифференциального уравнения высокого порядка с малыми параметрами при старших производных или системы дифференциальных уравнений первого порядка, разрешенных относительно производных, с малым параметром при части производных (самый распространенный вид):

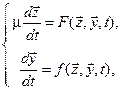(3.1)

где 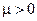- малый параметр, 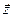и 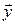- вектор-функции произвольных размерностей, .

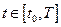Модель (3.1) в математической литературе принято называть тихоновской системой уравнений, а члены уравнений, содержащие малый параметр 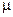, - возмущениями [1]. Для моделей вида (3.1) существует математическое обоснование возможности понижения порядка, основанное на теореме Тихонова о предельном переходе [1]. Эта теорема дает достаточные условия близости вне малой окрестности начальной точки 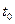(эта малая окрестность называется пограничным слоем) решений исходной сингулярно возмущенной модели к решениям вырожденной модели более низкого порядка, получаемой из (3.1), если положить 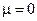. Однако на практике при описании реальных динамических систем их математические модели естественным образом получаются в виде систем в нормальной форме Коши:

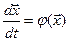, (3.2)

где 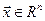- вектор переменных состояния, ,

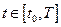то есть не содержат возмущения в явном виде. Поэтому возникает задача определения принадлежности модели системы, заданной в нормальной форме Коши (3.2), к сингулярно возмущенным с представлением возмущения в неявном виде. При положительном решении этой задачи она имеет естественное продолжение – нахождение вырожденной модели. Универсальные методы решения данных задач отсутствуют.

Настоящая лабораторная работа посвящена решению первой из указанных задач. Объектом исследования является математическая модель энергоблока ТЭС СГ2-500-4У2, заданная системой нелинейных дифференциальных уравнений в нормальной форме Коши (3.2). Ставится задача определения принадлежности модели, описывающей свободные составляющие процессов в энергоблоке, к классу сингулярно возмущенных с представлением возмущения в неявном виде.

Суть разработанной методики исследования состоит в следующем [2, 3]. Пусть имеется модель системы в режиме свободного движения, представленная системой нелинейных дифференциальных уравнений в нормальной форме Коши (3.2) с заданной областью 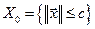начальных условий 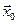. Рассмотрим некоторую реализацию процесса в системе и соответствующее ей решение (3.2) 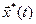, определяемое начальными условиями 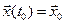из области .

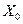Разобьем отрезок времени 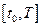, на котором рассматривается модель, на 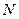малых частей точками 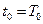, , 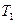, 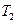…, 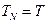. На каждом из отрезков 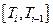, , 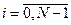линеаризуем систему уравнений (3.2) в окрестности точки 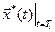. Получим N моделей в отклонениях – линейных систем с постоянными коэффициентами:

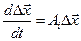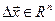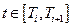, , , (3.3)

где , ,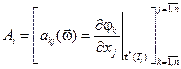

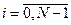с решениями 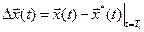при начальных условиях .

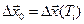Пусть модель (3.2) имеет вид

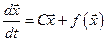, (3.4)

где нелинейные функции в правой части (3.4) не имеют переменных, соответствующих производным уравнения. Тогда для данного класса моделей систем может быть сформулировано необходимое и достаточное условие принадлежности к сингулярно возмущенным. Оно заключается в следующем.

Для того чтобы модель системы (3.2) в области 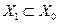(через 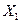обозначена область переменных 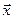, близкая к 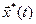) являлась сингулярно возмущенной, необходимо и достаточно, чтобы у матриц 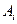, , 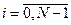линеаризованных моделей (3.3) существовало хотя бы одно собственное значение, удовлетворяющее условию

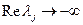. (3.5)

При этом порядок исходной модели может быть понижен на величину, равную числу корней, удовлетворяющих условию (3.5).

Если не накладывать ограничений на вид модели (3.2) (т.е. не ограничиваться рассмотрением систем вида (3.4.)), то условие (3.5) является необходимым условием принадлежности модели нелинейной динамической системы к сингулярно возмущенным.

На практике условие (3.5) можно заменить более реальным условием наличия у всех линеаризованных моделей (3.3) левых корней характеристических уравнений, сильно удаленных от остальных. Назовем такие корни доминирующими. В дальнейшем в качестве признака доминантности корня 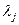будем принимать условие

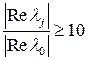, (3.6)

где 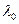- наиболее левый корень из группы не выделяющихся корней.

Математическая модель, описывающая работу электрической части энергоблока СГ2-500-4У2, представляет собой систему нелинейных дифференциальных уравнений в нормальной форме Коши 12-го порядка [4]:

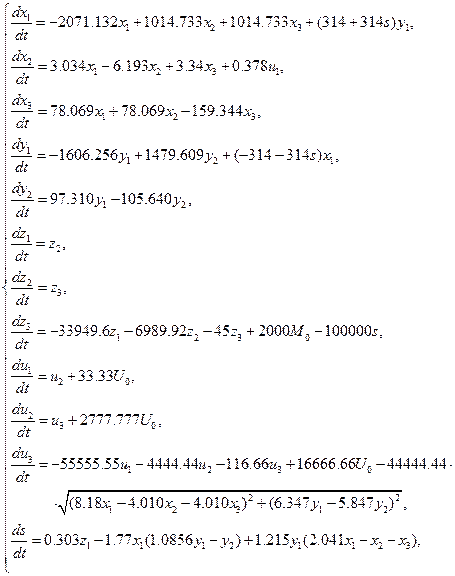(3.7)

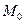где и 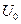- входные воздействия, а переменные состоянию имеют следующий физический смысл: 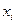, , 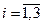, , 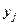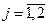- проекции потокосцеплений на оси координат; 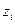, , 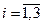- соответственно момент турбины, его первая и вторая производные; 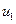- напряжение возбудителя; 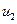и 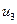- внутренние переменные автоматического регулятора частоты вращения; 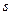- скольжение.

Поскольку в дальнейшем нас будет интересовать определение принадлежности модели, описывающей свободные составляющие процессов в энергоблоке, к классу сингулярно возмущенных, обнулим входные воздействия 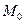и 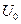и представим модель (3.7) в более удобном виде

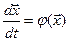, (3.8)

где 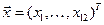, т.е. компонентами вектора 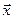являются все переменные состояния энергоблока, а вектор-функция 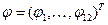состоит из правых частей системы уравнений (3.7), взятых пр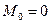и и .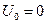

Модель (3.8) описывает свободные составляющие процессов в энергоблоке.

При выполнении п. 1 программы исследований требуется реализовать модель энергоблока на базе средств MATLAB/Simulink. Это можно сделать, например, с помощью редактора дифференциальных уравнений DEE (Differential Equation Editor). Данный редактор позволяет задавать системы дифференциальных уравнений в нормальной форме Коши и выполнять их решение. Для вызова редактора дифференциальных уравнений в командной строке MATLAB необходимо набрать dee и нажать Enter. Затем блок редактора помещается в окно с собираемой моделью. Далее в окно редактора DEE нужно ввести размерность вектора входных сигналов, систему уравнений, описывающую энергоблок, начальные условия и уравнения для расчета выходных сигналов.

В п. 1.1 задания на исследование математическая модель энергоблока рассматривается при наличии входных воздействи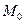й и 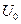, т.е. имеет вид (3.7). Соответствующая схема приведена на рис.3.1.

Рис.3.1

Блок Step реализует входные воздействия на систему в виде ступенчатого сигнала и имеет следующие параметры: Step time (время подачи ступеньки) = ”0”, Initial value (начальное значение) = ”0”, Final value (конечное значение) = ”1”.

Особенностью редактора дифференциальных уравнений DEE является использование «машинных переменных»: переменные состояния обозначаются вектором 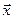, а входные воздействия – вектором 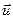. В рассматриваемой задаче выходные переменные редактора равны переменным состояния энергоблока. На рис.3.2 показано окно редактора DEE для пункта 1.1 программы исследований.

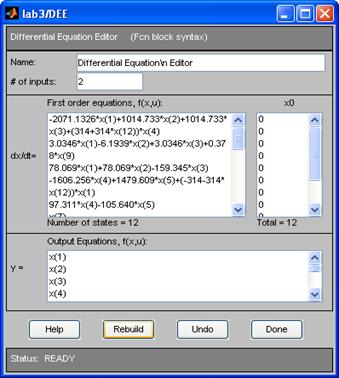
Рис.3.2

Правая часть математической модели энергоблока в «машинных переменных» приведена в Приложении (ВАЖНО: при каждом обращении к редактору DEE система уравнений и начальные условия «перемешиваются» и для данного примера модели физической системы – модели энергоблока - возникает «ошибка моделирования». В связи с этим после каждого открытия окна редактора DEE следует заново вставлять в него приведенные в Приложении правые части модели энергоблока).

При моделировании полученной системы рекомендуется использовать решатель ode45.

Результаты моделирования приведены на рис. 3.3, 3.4 и 3.5. В протоколе необходимо зафиксировать вид графиков переменных состояния энергоблока (при этом рекомендуется сохранить несколько графиков в различных масштабах так, чтобы по ним можно было судить о характере изменения всех переменных состояния).

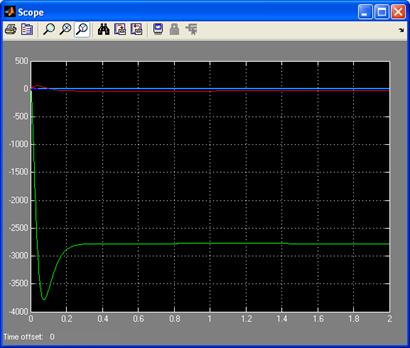
Рис.3.3 Графики переменных состояния энергоблока при наличии входных воздействий и нулевых начальных условиях.

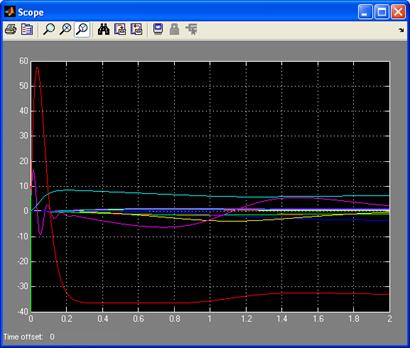
Рис.3.4 Графики переменных состояния энергоблока при наличии входных воздействий и нулевых начальных условиях (в увеличенном масштабе).

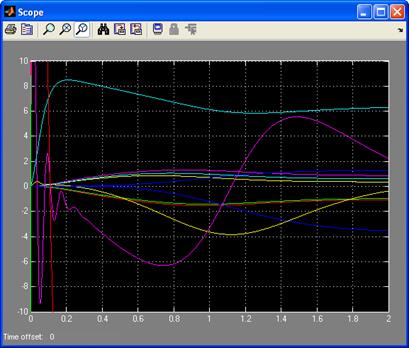
Рис.3.5 Графики переменных состояния энергоблока при наличии входных воздействий и нулевых начальных условиях (в увеличенном масштабе).

По снятым графикам требуется определить установившиеся значения каждой переменной состояния. Эти установившиеся значения берутся в качестве начальных значений для переменных состояния в пункте 1.2. программы исследований. Схема модели, описывающей свободные составляющие процессов в энергоблоке, изображена на рис.3.6.

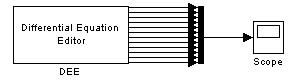
Рис.3.6

В п. 2 задания требуется проверить модель (3.8), описывающую свободные составляющие процессов в энергоблоке, на предмет принадлежности ее к классу сингулярно возмущенных. При выполнении данного пункта также используется схема, изображенная на рис. 3.6. Алгоритм проверки следующий:

1. Задание начальных условий (из п. 1.2) и выбор в качестве исследуемых процессов реализаций при данных начальных условиях.

2. Разбиение интервала времени, на котором рассматривается модель, на 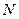малых отрезков 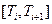, , 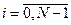и замена на каждом из них нелинейной модели (3.8) линейной моделью (3.3) (при этом матрица 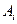составляется из вычисленных в точках 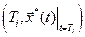частных производных , , ).

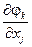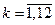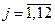3. Нахождение корней характеристических уравнений всех линеаризованных моделей и проверка их на доминантность (т.е. проверка выполнения условия (3.6)). Наличие доминантных корней свидетельствует о том, что исходная нелинейная модель (3.8), описывающая свободные составляющие процессов в энергоблоке, является сингулярно возмущенной и при выполнении определенных условий ее порядок может быть понижен.

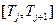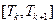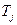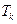В рамках лабораторной работы для сокращения вычислений рассматриваются только 2 отрезка времени: и , начальные моменты и которых задаются (по вариантам) таблицей 3.1 (Исходные данные для проведения исследований). Однако следует помнить о том, что вывод о принадлежности модели (3.8) к классу сингулярно возмущенных теоретически должен быть сделан на основании анализа собственных значений матриц линеаризованных на всех 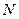отрезках моделей.

Для вычисления собственных значений матриц 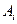(т.е. для нахождения корней характеристических уравнений линеаризованных моделей) можно использовать функцию eig:

sobstzn=eig(VPA(A)) – формирует символьный вектор sobstzn собственных значений квадратной матрицы A.