Основными позиционными задачами называются задачи, в которых определяются взаимное расположение точек, прямых и плоскостей. Существует всего 6 основных позиционных задач: взаимное расположение точек; взаимное расположение точки и прямой; взаимное расположение прямых; взаимное расположение точки и плоскости; взаимное расположение прямой и плоскости; взаимное расположение плоскостей. Различают позиционные задачи на принадлежность, параллельность и пересечение.
4.1. Конкурирующие точки. Определение видимости на эпюре
 |  | ||
У двух различных точек могут совпадать фронтальные проекции
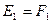 . Такие точки, расположенные на фронтально проецирующей прямой,
. Такие точки, расположенные на фронтально проецирующей прямой, Рис. 4.1 Рис. 4.1.2
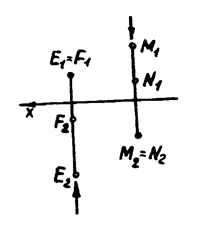
называются фронтально конкурирующими точками. При этом на 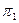 будет видима точка, горизонтальная проекция которой расположена ниже (рис.4.1). У двух различных точек М и
будет видима точка, горизонтальная проекция которой расположена ниже (рис.4.1). У двух различных точек М и 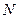 могут совпадать горизонтальные проекции
могут совпадать горизонтальные проекции 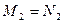 . Такие точки, расположенные на горизонтально проецирующей прямой, называются горизонтально конкурирующими точками. Из двух горизонтально конкурирующих точек на горизонтальной плоскости проекций будет видима точка, у которой фронтальная проекция расположена выше. Таким образом, на фронтальной проекции будет видима точка Е, а на горизонтальной проекции- точка М (рис. 4.1).
. Такие точки, расположенные на горизонтально проецирующей прямой, называются горизонтально конкурирующими точками. Из двух горизонтально конкурирующих точек на горизонтальной плоскости проекций будет видима точка, у которой фронтальная проекция расположена выше. Таким образом, на фронтальной проекции будет видима точка Е, а на горизонтальной проекции- точка М (рис. 4.1).
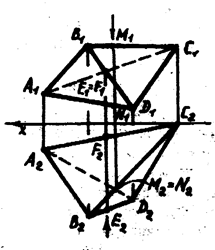
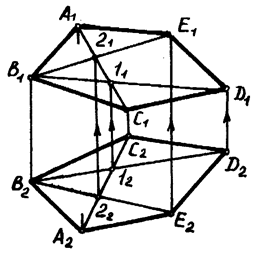
Для установления видимости на эпюре рассматриваются конкурирующие точки. Пусть требуется определить видимость ребер треугольной пирамиды 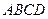 (рис. 4.1.2). Видимые на чертеже линии проводятся сплошными толстыми линиями, а невидимые линии – штриховыми линиями. Ясно, что контур фронтальной проекции – четырехугольник
(рис. 4.1.2). Видимые на чертеже линии проводятся сплошными толстыми линиями, а невидимые линии – штриховыми линиями. Ясно, что контур фронтальной проекции – четырехугольник 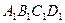 и контур горизонтальной проекции – четырехугольник
и контур горизонтальной проекции – четырехугольник 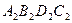 проводятся сплошными толстыми линиями. На фронтальной проекции из двух ребер
проводятся сплошными толстыми линиями. На фронтальной проекции из двух ребер 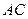 и
и 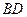 одно будет видимым, а другое невидимым. Рассматривая фронтально конкурирующие точки
одно будет видимым, а другое невидимым. Рассматривая фронтально конкурирующие точки 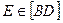 и
и 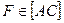 , видим, что горизонтальная проекция
, видим, что горизонтальная проекция 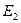 точки
точки 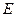 расположена ниже по сравнению с точкой
расположена ниже по сравнению с точкой 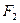 . Отсюда следует, что на плоскости
. Отсюда следует, что на плоскости 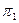 будет видимым ребро
будет видимым ребро 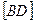 . Поэтому
. Поэтому 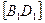 проводится сплошной толстой линией, а
проводится сплошной толстой линией, а 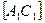 - штриховой линией. На горизонтальной проекции конкурирующими являются ребра
- штриховой линией. На горизонтальной проекции конкурирующими являются ребра 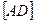 и
и 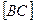 . С помощью точек
. С помощью точек 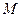 и
и 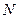 устанавливаем, что отрезок
устанавливаем, что отрезок 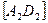 следует проводить штриховой линией, так как на плоскости
следует проводить штриховой линией, так как на плоскости 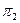 ребро
ребро 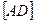 будет невидимым.
будет невидимым.
4.2. Взаимное расположение точки и прямой.
На рис. 4.2 изображены прямая l и три точки А, В и С. Точка А расположена впереди прямой l, точка В – над прямой l и точка С Î l.
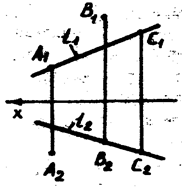 |
Рис.4.2
4.3. Взаимное расположение двух прямых.
Две прямые могут быть параллельными между собой. Тогда согласно 4 свойства одноименные проекции этих прямых должны располагаться параллельно: 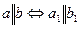 и
и 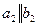 (рис. 4.3,а). Если прямые пересекаются, то точки пересечения одноименных проекций должны располагаться на прямой, перпендикулярной к оси Ох:
(рис. 4.3,а). Если прямые пересекаются, то точки пересечения одноименных проекций должны располагаться на прямой, перпендикулярной к оси Ох: 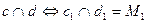 ,
, 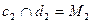 ,
, 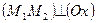 . Если последние условие не выполняется, то прямые скрещиваются. Для прямых
. Если последние условие не выполняется, то прямые скрещиваются. Для прямых 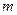 и
и 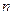 имеем, что
имеем, что 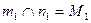 ,
, 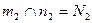 и
и 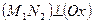 . Поэтому
. Поэтому 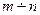 (рис. 4.3,в).
(рис. 4.3,в).
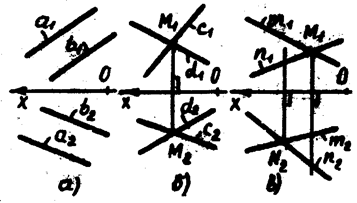 |
Рис. 4.3
4.4. Модель плоскости. Взаимное положение точки и плоскости.
Между фронтальной и горизонтальной проекциями плоскости общего положения устанавливается взаимно однозначное соответствие. Это соответствие обладает всеми свойствами родства. Поэтому говорят, что на эпюре Монжа плоскость моделируется родством. Каждой точке 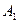 на фронтальной проекции соответствует определенная точка
на фронтальной проекции соответствует определенная точка 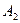 на горизонтальной проекции. Наоборот, каждой точке
на горизонтальной проекции. Наоборот, каждой точке 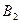 на горизонтальной проекции соответствует определенная точка
на горизонтальной проекции соответствует определенная точка 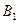 на фронтальной проекции. Прямой
на фронтальной проекции. Прямой 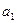 на плоскости
на плоскости 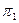 соответствует прямая
соответствует прямая 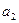 плоскости
плоскости 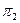 и наоборот. Кроме того, если
и наоборот. Кроме того, если 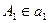 , то
, то 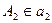 . Родство может быть задано: тремя точками, точкой и прямой, двумя параллельными или пересекающимися прямыми.
. Родство может быть задано: тремя точками, точкой и прямой, двумя параллельными или пересекающимися прямыми.
 |  | ||
Точка принадлежит плоскости или располагается вне нее. Известно, что если
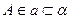 , то
, то 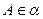 . Если точка
. Если точка 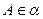 , то проекции
, то проекции 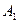 и
и 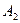 этой точки
этой точки 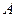 будут соответственными точками в родстве, определяемом плоскостью
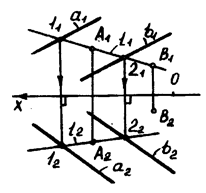
будут соответственными точками в родстве, определяемом плоскостью 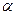 . Рассмотрим плоскость
. Рассмотрим плоскость 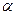 , которая задана параллельными прямыми
, которая задана параллельными прямыми 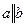 (рис. 4.4). Для определения принадлежности точки
(рис. 4.4). Для определения принадлежности точки 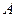 плоскости
плоскости 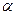 (
( 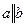 ) проводим через точку
) проводим через точку 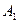 произвольную прямую
произвольную прямую 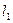 (или
(или 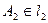 ) и находим прямую
) и находим прямую 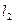 ,
, Рис. 4.4 Рис. 4.5
соответствующую ей родстве, определяемом плоскостью 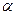 . Если
. Если 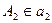 , то точка
, то точка 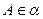 . Точка
. Точка 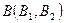 не принадлежит плоскости
не принадлежит плоскости 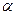 , так как
, так как 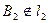 . По модели (чертежу) плоскости можно
. По модели (чертежу) плоскости можно
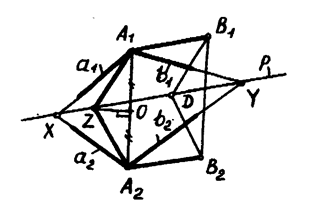
построить ось родства и изометрические направления. Пусть некоторая плоскость 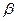 моделируется проекциями пересекающихся в точке А прямых а и
моделируется проекциями пересекающихся в точке А прямых а и 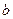 (рис. 4.5). Ось родства – это множество двойных (сама себе соответствующих) точек. Прямые
(рис. 4.5). Ось родства – это множество двойных (сама себе соответствующих) точек. Прямые 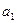 и
и 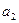 пересекаются в точке Х, а прямые
пересекаются в точке Х, а прямые 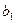 и
и 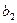 в точке
в точке 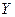 . Прямая р, соединяющая двойные точки Х и
. Прямая р, соединяющая двойные точки Х и 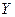 , будет осью родства. Родство в общем случае не сохраняет длину отрезка. Но имеются два направления, называемые изометрическими. Соответственные отрезки, параллельные этим направлениям будут конгруэнтными. Одно направление параллельно оси родства:
, будет осью родства. Родство в общем случае не сохраняет длину отрезка. Но имеются два направления, называемые изометрическими. Соответственные отрезки, параллельные этим направлениям будут конгруэнтными. Одно направление параллельно оси родства: 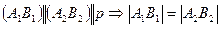 . Для определения другого направления проводим серединный перпендикуляр отрезка
. Для определения другого направления проводим серединный перпендикуляр отрезка 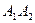 , который пересекает ось родства в точке
, который пересекает ось родства в точке 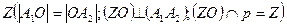 . Тогда
. Тогда 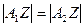 , прямые
, прямые 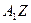 и
и 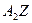 определяют второе изометрическое направление. Соответственные отрезки, параллельные этому направлению, будут равными между собой. Например, если через точку
определяют второе изометрическое направление. Соответственные отрезки, параллельные этому направлению, будут равными между собой. Например, если через точку 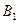 провести прямую, параллельную прямой
провести прямую, параллельную прямой 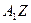 , до пересечения с осью р в точке
, до пересечения с осью р в точке 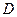 и соединить эту точку с точкой
и соединить эту точку с точкой 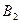 , то
, то 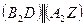 и
и 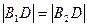 .
.
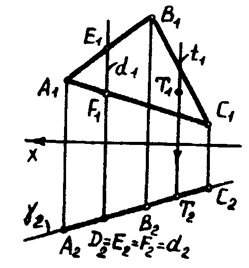 |  | ||
Рассмотрим соответствие, возникающее между проекциями плоскостей частного положения. Как было показано выше одной из проекций плоскости частного положения будет прямая линия. По чертежу можно определить, что треугольник
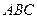 расположен перпендикулярно к горизонтальной плоскости проекции (рис. 4.6). Этот треугольник определяет некоторую горизонтальную проецирующую плоскость
расположен перпендикулярно к горизонтальной плоскости проекции (рис. 4.6). Этот треугольник определяет некоторую горизонтальную проецирующую плоскость 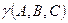 . Если задана горизонтальная
. Если задана горизонтальная Рис. 4.6 Рис. 4.7
проекция 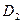 точки
точки 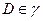 , то на фронтальной проекции ей соответствует множество точек
, то на фронтальной проекции ей соответствует множество точек 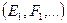 , расположенных на вертикальной прямой
, расположенных на вертикальной прямой 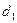 . При этом можно сказать, что точке соответствует прямая. Если задана фронтальная проекция
. При этом можно сказать, что точке соответствует прямая. Если задана фронтальная проекция 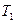 точки
точки 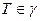 , то на горизонтальной проекции ей соответствует точка
, то на горизонтальной проекции ей соответствует точка 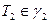 . При этом любая точка вертикальной прямой
. При этом любая точка вертикальной прямой 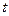 проецируется на плоскость
проецируется на плоскость 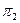 в точку
в точку 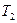 . Таким образом, плоскость частного положения на эпюре Монжа моделируется также соответствием, в котором прямой соответствует точка и, наоборот, точке соответствует прямая. Такое соответствие будем называть вырожденным родством. Плоскость частного положения на чертеже моделируется вырожденным родством.
. Таким образом, плоскость частного положения на эпюре Монжа моделируется также соответствием, в котором прямой соответствует точка и, наоборот, точке соответствует прямая. Такое соответствие будем называть вырожденным родством. Плоскость частного положения на чертеже моделируется вырожденным родством.
Пример. Достроить фронтальную проекцию плоского пятиугольника 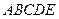 , если задана ее горизонтальная проекция
, если задана ее горизонтальная проекция 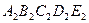 и фронтальные проекции трех вершин
и фронтальные проекции трех вершин 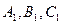 .
.
Решение. Три пары соответственных точек 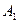 и
и 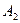 ,
, 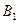 и
и 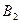 ,
, 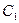 и
и 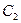 определяют родство. Надо найти точки
определяют родство. Надо найти точки 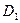 и
и 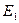 , соответствующие точкам
, соответствующие точкам 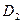 и
и 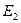 в родстве, заданном тремя парами соответственных точек
в родстве, заданном тремя парами соответственных точек 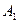 и
и 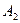 ,
, 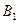 и
и 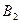 ,
, 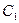 и
и 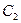 (рис. 4.7). Проводим диагонали
(рис. 4.7). Проводим диагонали 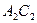 ,
, 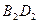 и
и 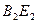 , которые пересекаются в точках
, которые пересекаются в точках 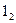 и
и 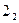 . Фронтальные проекции
. Фронтальные проекции 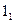 и
и 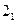 находятся на отрезке
находятся на отрезке 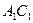 . Прямая, соединяющая точки
. Прямая, соединяющая точки 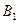 и
и 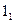 , пересекает прямую, проведенную параллельно направлению родства в точке
, пересекает прямую, проведенную параллельно направлению родства в точке 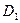 . Аналогично определяется точка
. Аналогично определяется точка 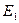 . Теперь остается соединить точку
. Теперь остается соединить точку 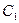 с точкой
с точкой 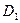 , точку
, точку 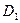 с точкой
с точкой 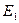 и точку
и точку 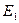 с точкой
с точкой 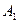 .
.
 |
4.5. Прямая, принадлежащая плоскости
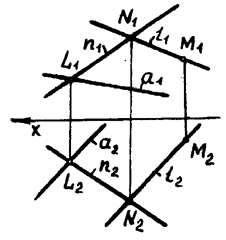 |
Рис. 4.8 Рис. 4.9
Для того чтобы прямая принадлежала плоскости, необходимо и достаточно, чтобы две различные точки этой прямой принадлежали плоскости: 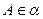 и
и 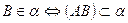 . Прямая
. Прямая 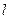 принадлежит плоскости
принадлежит плоскости 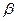 , заданной точкой М и прямой
, заданной точкой М и прямой 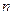 (рис. 4.8), так как две точки М и
(рис. 4.8), так как две точки М и 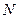 этой прямой лежат на плоскости
этой прямой лежат на плоскости 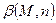 . Имеется еще один признак принадлежности прямой плоскости: для того чтобы прямая принадлежала плоскости, необходимо и достаточно, чтобы она прошла через одну из точек этой плоскости и была параллельна прямой, принадлежащей этой плоскости или параллельна ей. Поэтому прямая а не принадлежит плоскости
. Имеется еще один признак принадлежности прямой плоскости: для того чтобы прямая принадлежала плоскости, необходимо и достаточно, чтобы она прошла через одну из точек этой плоскости и была параллельна прямой, принадлежащей этой плоскости или параллельна ей. Поэтому прямая а не принадлежит плоскости 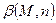 , хотя
, хотя 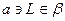 и
и 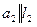 . Это объясняется тем, что
. Это объясняется тем, что 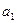 не параллельна
не параллельна 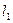
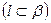 (рис.4.8). Нужно отметить, что проекции прямой, принадлежащей плоскости, будут соответственными прямыми в родстве, определяемом этой плоскостью.
(рис.4.8). Нужно отметить, что проекции прямой, принадлежащей плоскости, будут соответственными прямыми в родстве, определяемом этой плоскостью.
Прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций, называется фронталью этой плоскости. В плоскости можно провести множество фронталей, одноименные проекции которых будут параллельными между собой. 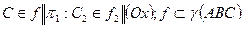 .
. 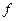 - фронталь плоскости
- фронталь плоскости 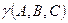 .
. 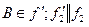 и
и 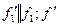 - другая фронталь плоскости
- другая фронталь плоскости 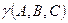 .
.
Прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций, называется горизонталью этой плоскости (рис. 5.10).
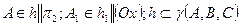 .
. 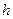 - одна из горизонталей плоскости
- одна из горизонталей плоскости 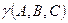 .
.
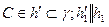 и
и 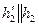 .
. 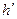 - другая горизонталь плоскости
- другая горизонталь плоскости 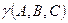 .
.
Через прямую общего положения можно провести единственную фронтально проецирующую плоскость и единственную горизонтально проецирующую плоскость, которые пересекаются по этой прямой общего положения.
4.6. Прямая параллельная плоскости.
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой этой плоскости. Чтобы задача имела единственное решение нужно иметь дополнительное условие. На рис. 4.9 показаны построения прямых параллельных плоскостям проекций. Пусть требуется определить проекции прямой 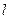 , проходящей через точку
, проходящей через точку 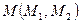 и параллельной плоскости
и параллельной плоскости 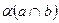 (рис. 4.11), если горизонтальная проекция
(рис. 4.11), если горизонтальная проекция 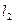 этой прямой
этой прямой 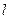 образуется с осью
образуется с осью 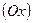
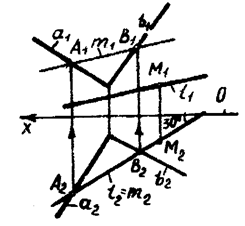 |
угол в 300. Через точку
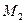 проводим прямую
проводим прямую 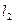 под углом 300 по отношению к оси
под углом 300 по отношению к оси 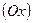 . Пусть она совпадает с прямой
. Пусть она совпадает с прямой 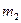 - горизонтальной проекцией прямой
- горизонтальной проекцией прямой 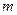 , принадлежащей плоскости
, принадлежащей плоскости 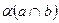 . Определяем фронтальную проекцию
. Определяем фронтальную проекцию 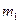 , которая проходит через точки
, которая проходит через точки 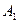 и
и 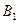 . Через точку
. Через точку 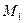 проводим
проводим 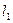 параллельно прямой
параллельно прямой 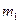 . Тогда прямая
. Тогда прямая 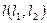 будет искомой, так как она проходит через точку
будет искомой, так как она проходит через точку 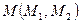 и параллельна плоскости
и параллельна плоскости 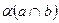 .
. Основная литература: 1[24-33]
Дополнительная литература: 3[17-47].
Контрольные вопросы:
1. Что такое «первая позиционная задача начертательной геометрии»? Что такое вторая?
2. Каким методом определяют видимость элементов фигур на эпюре?
3. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.
4. Какие вы знаете свойства плоских углов? Теорема о прямом угле, что это такое?
5. Какие параметры определяют «методом прямоугольного треугольника»?
 2015-05-12
2015-05-12 2574
2574






