2015-05-12
3495.1 Построение точки пересечения прямой и плоскости
В начале рассмотрим взаимное расположение прямой и проецирующей плоскости. Здесь возможны три случая: вырожденная в прямую проекция плоскости и соответствующая проекция прямой могут совпадать, располагаться или пересекаться. В зависимости от этого прямая принадлежит плоскости, располагается ей параллельно или они пересекаются.
Найти точку пересечения прямой и плоскости – это означает, что нужно определить такую точку, принадлежащую данной прямой, и проекции которой будут находиться в соответствии, установленном данной плоскостью.
|
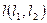и плоскости 
.
 |
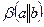Отнесем прямую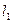 
полю фронтальной проекции плоскости 
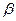и обозначим через 
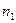. Определим прямую 
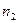, родственную прямую 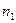в соответствии, установленном плоскостью 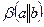. Таким образом, задача сводится к определению взаимного расположения прямых 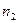и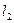 
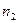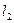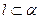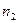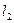. Если = , то 
; || , то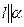 
. На нашем примере 
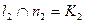. С помощью линии связи, проведенной через точку 
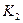, определена точка 
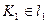. Точка 
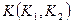является искомой точкой пересечения прямой 
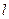и плоскости : 
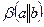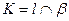. Невидимые на эпюре части прямой проведены штриховой линией. Для установления видимости на фронтальной проекции использованы фронтально конкурирующие точки 1 и 3, с на горизонтальной проекции – горизонтально конкурирующие точки 4 и 5.
|
|
|
Аналогично определяется точка пересечения прямой 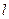и плоскости 
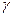, заданной своими следами (рисунок 5.1). Прямой 
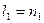, отнесенной фронтальной проекции плоскости 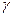, соответствует прямая 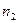; прямая 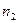проходит через точки 
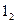и 
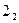. Точка пересечения прямых 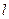и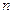 
будет искомой точкой: 
; 
; 
; 
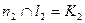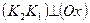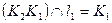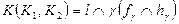. Часть прямой 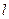, которая начинается из точки 
и расположена ниже плоскости 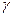, будет невидимой.
5 .2 Построение линии пересечения двух плоскостей.
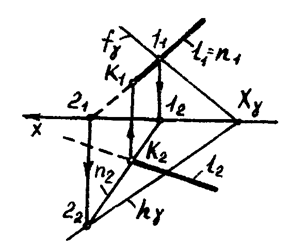
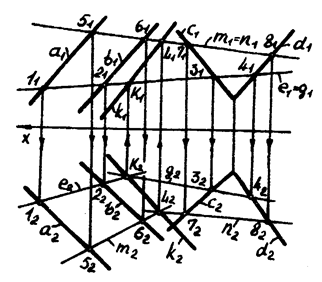
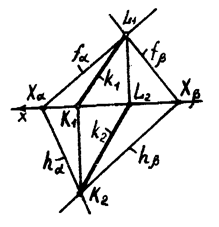
На рисунке 5.1 изображены две плоскост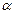и 
и 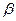, первая из которых задана параллельными прямым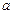и 
и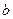 
, а вторая – пересекающимися прямым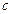и 
и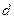 
. Требуется установить взаимное расположение этих плоскосте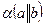й 
и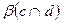 
.
Здесь мы имеем два родственных соответствия, порождаемые соответственно плоскостям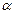и и 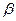. Нам надо определить общую прямую этих двух родственных соответствий. Проведем произвольную прямую 
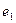и отнесем ее плоскости 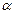. Тогда ей соответствует прямая 
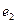в родстве, определяемым первой плоскостью. Затем отнесем прямую 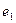второй плоскости и обозначим 
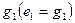. Находим соответствующую ей прямую 
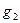в родстве, установленном второй плоскостью. Рассмотрим взаимное расположение двух прямых 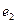и 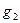. Возможны три случая:
1) 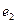= 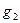; тогда плоскост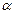и и 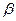совпадают ( = );
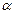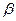2) 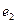Ç 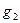= 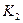; тогда точка К принадлежит линии пересечения плоскостей: 
;
|
|
|
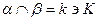3) || .
 |  | ||
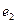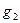В первом случае задача уже решена. Если имеет место второй или
Рисунок 5.1
третий случай, следует повторить построение, изменив положение прямой 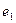на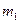 
. В случае, когда 
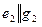необходимо выполнить условие 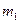не параллельна 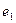. Находим прямую 
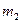плоскости 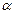, и прямую 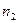, относя прямую 
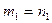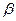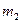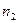плоскости . Теперь возможны два случая: 1) прямые и параллельны, тогда 
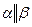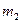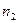; 2) прямые и пересекаются в точке 
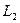. Точка 
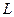принадлежит линии пересечения плоскостей: 
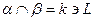. Во втором случае данные плоскости пересекаются по прямой 
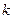, которая проводится через точк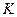и и 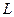или через точку 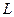параллельно прямым 
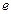и 
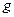(если ).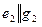
Пример 3. Построить линию пересечения плоскосте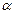й и 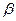, заданных своими следами (рисунок 5.2).
Решение. Точка пересечения 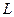фронтальных следов плоскостей и точка пересечения 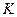горизонтальных следов плоскостей являются общими точками заданных плоскостей.
; 
.
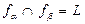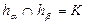Поэтому прямая 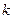, соединяющая точк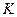и и 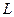, является искомой линией пересечения: 
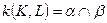. Этот результат является частным случаем выше приведенной общей схемы. Здесь за 
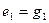принимается ось 
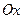; тогда 
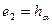и 
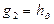. За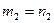 
принимается также ось 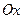, в результате этого 
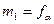и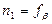 
.
Основная литература: 1[24-33]
Дополнительная литература: 3[17-47];
Контрольные вопросы:
1. Что такое «первая позиционная задача начертательной геометрии»? Что такое вторая?
2. Каким методом определяют видимость элементов фигур на эпюре?
3. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.
4. Какие вы знаете свойства плоских углов? Теорема о прямом угле, что это такое?
5. Какие параметры определяют «методом прямоугольного треугольника»?
