Пусть производится n независимых испытаний, в каждом из которых событие может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р (0< p < 1). Следовательно, вероятность непоявления события А в каждом испытании также постоянна и равна q = 1 – p.
Часто возникает задача вычислить вероятность того, что при n испытаниях событие А наступит ровно k раз.
Искомая вероятность обозначается P  (k).
(k).
Например, символ Р 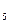 (3), означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
(3), означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
P  (k) =
(k) = 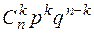 ,
,
где 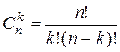 .
.
Вероятности того, что в n испытаниях событие наступит: а)менее t раз; б) более t раз; в) не менее t раз; г) не более t раз находят соответственно по формулам:
a) P  (0) + P
(0) + P  (1)+…+ P
(1)+…+ P  (t–1)= P
(t–1)= P  (k<t),
(k<t),
б) P  (t+1) + P
(t+1) + P  (t+2) + … + P
(t+2) + … + P  (n) = P
(n) = P  (k>t),
(k>t),
в) P  (t) + P
(t) + P  (t +1) + … + P
(t +1) + … + P  (n) = P
(n) = P  (k≥t),
(k≥t),
г) P  (0) + P
(0) + P  (1) +… + P
(1) +… + P  (t) = P
(t) = P  (k≤t).
(k≤t).
Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,7. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжении каждых из 6 суток постоянна и равна р=0,7. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q =1 – p = 1 – 0,7 = 0,3.
Из условия задачи следует, что n = 6; k=4.
Искомая вероятность по формуле Бернулли равна:
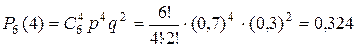 .
.
 2015-05-12
2015-05-12 1090
1090
