Определение. Будем говорить, что события В 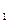 , В
, В 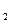 , …, В
, …, В  образуют полную группу событий, если:
образуют полную группу событий, если:
1. Событие В 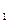 + В
+ В 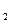 + …+ В
+ …+ В  достоверное;
достоверное;
2. События Вi и Вj – попарно несовместные (i= 1,2,…,n, j= 1,2,…,n, i 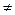 j).
j).
Утверждение. Сумма вероятностей событий, образующих полную группу равна 1.
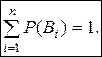
Пример. Студент на экзамене может получить одну из четырех оценок: «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно». События 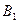 – получил «отлично»,
– получил «отлично»,
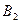 – получил «хорошо»,
– получил «хорошо»,
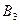 – получил «удовлетворительно»,
– получил «удовлетворительно»,
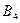 – получил «неудовлетворительно»
– получил «неудовлетворительно»
попарно несовместные и в сумме – событие достоверное, так как обязательно происходит одно из этих событий. Следовательно, события В 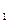 , В
, В 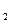 , В
, В 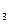 , В4 образуют полную группу событий.
, В4 образуют полную группу событий.
Для нахождения вероятности события А, которое может произойти при условии осуществления одного из несовместных событий В 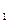 , В
, В 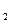 , …, В
, …, В  , образующих полную группу, используется формула:
, образующих полную группу, используется формула:
Р(А)= 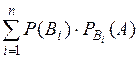
Эта формула называется формулой полной вероятности.
События В 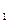 , В
, В 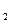 , …, В
, …, В  называются гипотезами.
называются гипотезами.
Пример. В урну, содержащую два шара, опущен зеленый шар. Найти вероятность того, что будет вытащен из урны зеленый шар, если равновероятны первоначальные представления о цвете шаров.
Решение. Событие А– извлечен зеленый шар.
Возможны следующие гипотезы о первоначальном составе шаров:
В 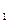 – первоначально зеленых шаров не было в урне;
– первоначально зеленых шаров не было в урне;
В 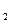 – был 1 зеленый шар;
– был 1 зеленый шар;
В 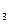 – оба шара зеленые.
– оба шара зеленые.
По условию задачи гипотезы равновероятны и образуют полную группу событий, следовательно, вероятность каждой из гипотез равна ⅓, то есть Р(В 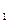 )= Р(В
)= Р(В 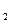 ) = Р(В
) = Р(В 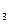 ) = ⅓. Тогда условные вероятности наступления события А при появлении каждой из гипотез будут соответственно равны:
) = ⅓. Тогда условные вероятности наступления события А при появлении каждой из гипотез будут соответственно равны:
Р 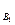 (А) = ⅓; Р
(А) = ⅓; Р 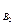 (А) = ⅔; Р
(А) = ⅔; Р 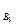 (А) =1.
(А) =1.
Отсюда по формуле полной вероятности получаем:
Р(А) = Р(В 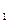 ) · Р
) · Р 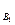 (А) + Р(В
(А) + Р(В 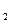 ) · Р
) · Р 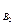 (А) + Р(В
(А) + Р(В 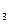 ) · Р
) · Р 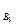 (А).
(А).
Р(А) = ⅓ · ⅓ + ⅓ · ⅔ + ⅔ · 1 = ⅔.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий В 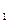 , В
, В 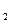 , …, В
, …, В  , образующих полную группу событий.
, образующих полную группу событий.
Если событие А уже произошло, то вероятности гипотез В 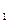 , В
, В 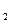 , …, В
, …, В  могут быть переоценены по следующей формуле:
могут быть переоценены по следующей формуле:
Р 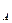 (B
(B 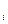 )=
)= 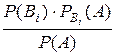 ,
,
где i = 1, 2, 3,…, n.
Эта формула называется формулой Байеса.
Пример. Два автомата производят одинаковые детали, поступающие на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй 84%. Наудачу взятая деталь оказалась отличного качества. Найти вероятность того, что эта деталь сделана первым автоматом.
Решение. Рассмотрим событие А – деталь отличного качества.
Можно составить две гипотезы:
В 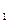 – деталь сделана первым автоматом, причем Р(В
– деталь сделана первым автоматом, причем Р(В 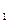 ) = ⅔, так как его производительность вдвое больше производительности второго автомата.
) = ⅔, так как его производительность вдвое больше производительности второго автомата.
В 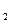 – деталь сделана вторым автоматом, причем Р(В
– деталь сделана вторым автоматом, причем Р(В 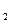 ) = ⅓.
) = ⅓.
Условная вероятность появления события А при выполнении гипотезы В 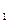 равна Р
равна Р 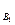 (А) = 0,6.
(А) = 0,6.
Условная вероятность появления события А при выполнении гипотезы В 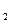 равна: Р
равна: Р 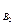 (А) = 0,84.
(А) = 0,84.
Отсюда вероятность появления события А равна:
Р(А) = ⅔ · 0,6 + ⅓ · 0,84 = 0,68.
Тогда вероятность того, что деталь отличного качества сделана первым автоматом, по формуле Байеса равна:
Р 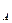 (В
(В 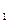 ) =
) = 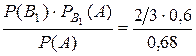 =
= 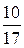 .
.
 2015-05-12
2015-05-12 672
672








