Пусть корень уравнения f(x)=0 отделен на отрезке 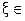 [a;b], то есть на этом отрезке имеется единственный корень, а функция на данном отрезке непрерывна.
[a;b], то есть на этом отрезке имеется единственный корень, а функция на данном отрезке непрерывна.
Метод половинного деления позволяет получить последовательность вложенных друг в друга отрезков [a1;b1], [a2;b2], …,[ai;bi],…, [an;bn], таких что f(ai).f(bi) < 0, где i=1,2,…,n, а длина каждого последующего отрезка вдвое меньше длины предыдущего:
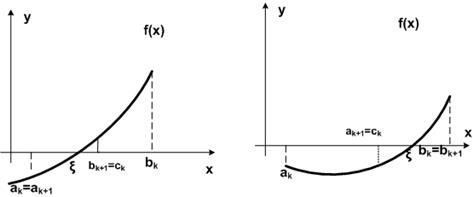
Рис.6.2.3-1
Последовательное сужение отрезка вокруг неизвестного значения корня 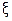 обеспечивает выполнение на некотором шаге n неравенства |bn - an| < e. Поскольку при этом для любого хÎ[an;bn] будет выполняться неравенство |
обеспечивает выполнение на некотором шаге n неравенства |bn - an| < e. Поскольку при этом для любого хÎ[an;bn] будет выполняться неравенство | 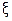 - х| <
- х| < 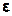 , то с точностью
, то с точностью 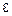 любое
любое
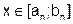 может быть принято за приближенное значение корня, например его середину отрезка
может быть принято за приближенное значение корня, например его середину отрезка 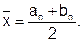
В методе половинного деления от итерации к итерации происходит последовательное уменьшение длины первоначального отрезка [a0;b0]в два раза (рис. 6.2.3-1). Поэтому на n-м шаге справедлива следующая оценка погрешности результата:
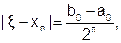 ( 6.2.3-1 )
( 6.2.3-1 )
где 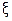 - точное значение корня, хnÎ [an;bn] – приближенное значение корня на n-м шаге.
- точное значение корня, хnÎ [an;bn] – приближенное значение корня на n-м шаге.
Сравнивая полученную оценку погрешности с заданной точностью 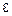 , можно оценить требуемое число шагов:
, можно оценить требуемое число шагов:
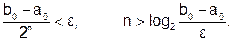 (6.2.3-2)
(6.2.3-2)
Из формулы видно, что уменьшение величины e (повышение точности) приводит к значительному увеличению объема вычислений, поэтому на практике метод половинного деления применяют для сравнительно грубого нахождения корня, а его дальнейшее уточнение производят с помощью других, более эффективных методов.
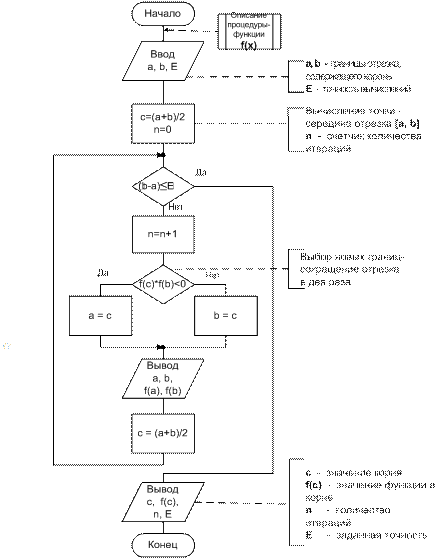 |
Рис. 6.2.3-2. Схема алгоритма метода половинного деления
Схема алгоритма метода половинного деления приведена на рис. 6.2.3-2. В приведенном алгоритме предполагается, что левая часть уравнения f(x)оформляется в виде программного модуля.
Пример 6.2.3-1. Уточнить корень уравнения x3+x-1=0 с точностью 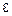 =0.1, который локализован на отрезке [0;1].
=0.1, который локализован на отрезке [0;1].
Результаты удобно представить с помощью таблицы 6.2.3-3.
Таблица 6.2.3-3
| k | a | b | f(a) | f(b) | (a+b)/2 | f((a+b)/2) | a k | b k |
| -1 | 0.5 | -0.375 | 0.5 | |||||
| 0.5 | -0.375 | 0.75 | 0.172 | 0.5 | 0.75 | |||
| 0.5 | 0.75 | -0.375 | 0.172 | 0.625 | -0.131 | 0.625 | 0.75 | |
| 0.625 | 0.75 | -0.131 | 0.172 | 0.688 | 0.0136 | 0.625 | 0.688 |
После четвертой итерации длина отрезка |b4-a4| = |0.688-0.625| = 0.063 стала меньше величины e, следовательно, за приближенное значение корня можно принять значение середины данного отрезка: x = (a4+b4)/2 = 0.656.
Значение функции f(x) в точке x = 0.656 равно f(0.656) = -0.062.
 2015-05-13
2015-05-13 1050
1050
