Глава IV
Аналитическая геометрия – область геометрии, в которой изучаемому геометрическому объекту (поверхности или линии) ставится в соответствие определённое уравнение или система уравнений, и исследование геометрических объектов сводится к исследованию соответствующих уравнений.
Одному и тому же геометрическому объекту могут быть отнесены уравнения разных типов: векторное, уравнение в декартовых координатах, векторно-параметрическое и скалярно-параметрическое и т.д.
Сказанное выше поясним на конкретных поверхностях и линиях.
1) Плоскост ь
Простейшей из поверхностей является плоскость. Рассмотрим различные типы уравнений плоскости и исследуем эти уравнения.
a) Векторное уравнение плоскости
Пусть в пространстве выбрана прямоугольная система координат xOyz и задан вектор 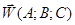 и т.
и т. 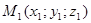 , а следовательно и радиус-вектор этой точки
, а следовательно и радиус-вектор этой точки 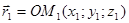 .
.
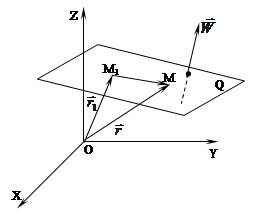 |
Очевидно, что существует только одна плоскость Q, которая проходит через т.
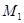 , и перпендикулярна вектору
, и перпендикулярна вектору 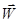 (прямой на которой он расположен).
(прямой на которой он расположен).
Вектор 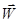 называется вектором плоскости Q.
называется вектором плоскости Q.
Пусть т. 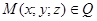 - текущая точка плоскости Q.
- текущая точка плоскости Q.
Очевидно, что 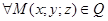 и данной
и данной 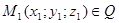 :
:
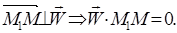
Т.к. 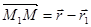 , где
, где 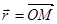 , тогда
, тогда

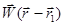 - векторное уравнение плоскости Q, заданной векторами
- векторное уравнение плоскости Q, заданной векторами 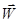 и
и 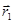 .
.
b) Уравнение плоскости в декартовых координатах
 Т.к.
Т.к. 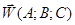 , а
, а 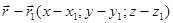 , то можно переписать через координаты векторов.
, то можно переписать через координаты векторов.

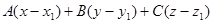 - уравнение в декартовых или уравнение плоскости, проходящие через данную т.
- уравнение в декартовых или уравнение плоскости, проходящие через данную т. 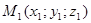 перпендикулярно вектору
перпендикулярно вектору 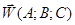 .
.
c) Общее уравнение плоскости

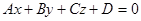 - общее уравнение плоскости
- общее уравнение плоскости
D – характеризует отдаленность плоскости.
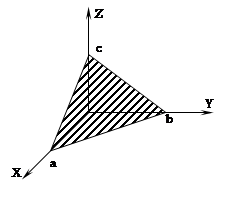
d) Уравнение плоскости в отрезках на осях
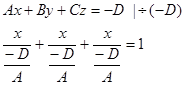
 |
Обозначим
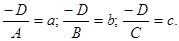 Получим
Получим 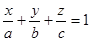 - уравнение плоскости в отрезках на осях.
- уравнение плоскости в отрезках на осях.
e) Векторно-параметрическое уравнение плоскости
Пусть в пространстве xOyz заданы два неколлинеарных вектора.
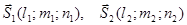 и т.
и т. 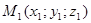 существует только одна плоскость, которая проходит через т.
существует только одна плоскость, которая проходит через т. 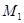 и параллельна векторам
и параллельна векторам 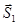 и
и 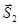 .
.
Рассмотрим векторы 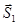 и
и 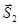
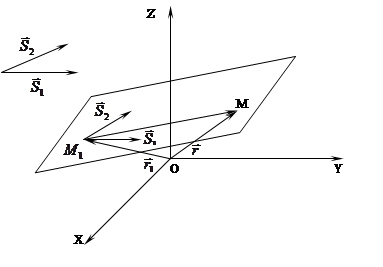 |
Пусть т.
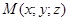 - любая текущая точка плоскости Q, тогда
- любая текущая точка плоскости Q, тогда

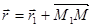 , где
, где 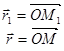
Векторы 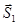 и
и 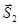 неколлинеарные следовательно образуют на плоскости Q векторный базис следовательно
неколлинеарные следовательно образуют на плоскости Q векторный базис следовательно 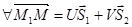 . Т.к. т.М любая, то скаляры U и V принимают независимо друг от друга любые действительные значение.
. Т.к. т.М любая, то скаляры U и V принимают независимо друг от друга любые действительные значение.
 Подставим в вместо
Подставим в вместо 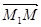 его разложение по векторам
его разложение по векторам 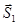 и
и 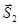 , получим:
, получим:

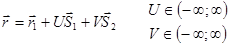 - векторно-параметрическое уравнение плоскости Q, которая задана вектором
- векторно-параметрическое уравнение плоскости Q, которая задана вектором 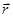 , точки
, точки 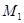 и векторами
и векторами 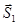 и
и 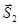 , которые называются направляющими векторами плоскости Q.
, которые называются направляющими векторами плоскости Q.
f)  Скалярно-параметрическое уравнение плоскости.
Скалярно-параметрическое уравнение плоскости.
Проектируяобе части уравнения на оси координат, получим скалярно-
параметрическое уравнение плоскости Q.

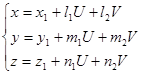
g) Другая форма записи уравнения плоскости в декартовых координатах.
Рассмотрим 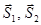 и
и 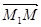 . Если т.
. Если т. 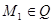 и т.
и т. 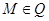 , то все эти три вектора компланарны.
, то все эти три вектора компланарны.
Условие компланарности трех векторов имеет вид:

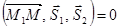
h) 
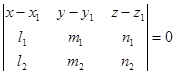 |
Условие параллельности, перпендикулярности двух плоскостей, угол между плоскостями.
Пусть даны две плоскости 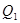 и
и 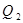 .
.
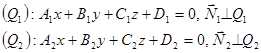
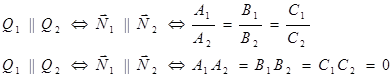

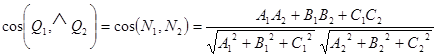
i)
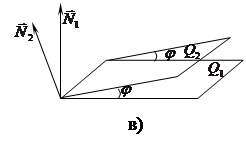 |
Исследование общего уравнения плоскости
Пусть плоскость Q задана уравнением
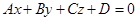 (**)
(**)
Как она расположена относительно системы координат xOyz, если некоторые коэффициенты уравнения (**) равны нулю?
1) 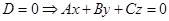 . В этом случае координаты т.
. В этом случае координаты т. 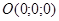 удовлетворяют этому уравнению
удовлетворяют этому уравнению 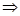 т.
т. 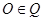 , т.е. плоскость Q проходит через начало координат.
, т.е. плоскость Q проходит через начало координат.
2) С=0: уравнение (**) примет вид:
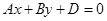 . В этом случае
. В этом случае 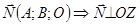 . Из
. Из 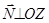 и
и 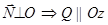 . Итак, если С=0
. Итак, если С=0 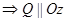 .
.
Аналогично:
3) 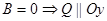
4) 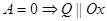
5) 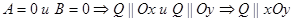
6) 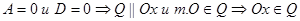
7) 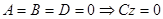 или z=0. В этом случае Q||xOy и т.
или z=0. В этом случае Q||xOy и т. 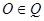 , т.е. Q совпадает с xOy и т.д.
, т.е. Q совпадает с xOy и т.д.
j) Расстояние от точки до плоскости
Пусть дана т. 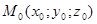 и плоскость (Q):
и плоскость (Q): 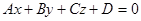 . Найти расстояние от т.
. Найти расстояние от т. 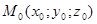 до (Q).
до (Q).
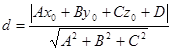
2) Прямая в пространстве
a) Уравнение прямой в декартовых координатах
Прямая (g) в пространстве может быть задана как линия пересечения двух плоскостей, заданных своими уравнениями в декартовых координатах:
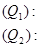
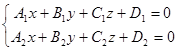
Символически это записывается так:
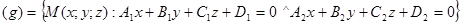
b) Векторно параметрическое уравнение прямой:
Пусть прямая задана т. 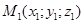 и направленным вектором
и направленным вектором 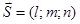 ,
, 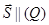 . Возьмем на прямой произвольную точку (текущую)
. Возьмем на прямой произвольную точку (текущую) 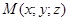 .
. 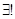 прямая проходящая через данную точку параллельному данному вектору.
прямая проходящая через данную точку параллельному данному вектору.
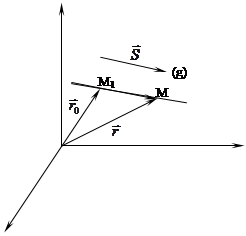

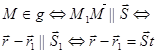
Когда параметр t принимает все значения из интервала 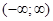 , т.М – пробегает прямую (g).
, т.М – пробегает прямую (g).
c)  Скалярно параметрическое уравнение прямой
Скалярно параметрическое уравнение прямой
Распишем проектируя обе части уравнения на оси координат. Пишим
скалярно-параметрическое уравнение прямой:

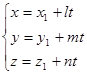
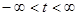
d) Каноническое уравнение прямой.
 Если из исключить параметр t то мы придём к уравнениям прямой в
Если из исключить параметр t то мы придём к уравнениям прямой в
канонической форме:

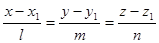
e) Уравнение прямой проходящее через две заданные точки.
Через две точки проходит единственная прямая.
 2015-05-13
2015-05-13 582
582






