|
Звуковая волна представляет собой последовательные сжатия и разрежения газа, происходящие с частотой от 20 до 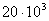 герц. Скорость распространения звуковой волны зависит от свойств газа. герц. Скорость распространения звуковой волны зависит от свойств газа.
Рассмотрим возникновение импульса сжатия в газе. Представим себе пластинку небольших размеров, помещенную в газ. Сообщив пластине быстрое перемещение параллельно ее плоскости, мы вызовем в прилегающем слое газа сжатие и, вследствие этого, фронт повышенного давления. Это давление вызовет движение следующего слоя и так далее. Сжатие и движение будут передаваться от слоя к слою. В газе, вправо от пластины, будет распространяться продольный импульс сжатия. Распространение импульса обусловлено наличием упругих сил, возникающих в газе. Газы обладают упругостью лишь в отношении объема и не обладают упругостью в отношении сдвига. Поэтому в газе будут распространяться только продольные импульсы. Скорость распространения продольного импульса в газе можно рассчитать. Пусть импульс сжатия соответствует увеличению плотности на 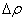 и увеличению давления на и увеличению давления на 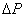 . Через площадку S, перпендикулярную к направлению распространения импульса, за время . Через площадку S, перпендикулярную к направлению распространения импульса, за время 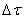 проходит часть импульса сжатия проходит часть импульса сжатия 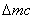 , где c – скорость распространения импульса (рис.1). , где c – скорость распространения импульса (рис.1).
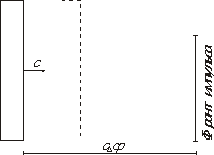
рис.1
Масса газа, расположенного справа от площадки S, возрастает на величину 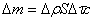 . При этом через площадку передается импульс . При этом через площадку передается импульс 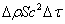 . .
Вместе с тем, слева на площадку действует сила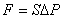 , ,
так как
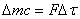 , ,
то
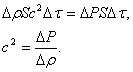 (1) (1)
Скорость перемещения импульса сжатия определяется тем, как изменяется плотность среды при изменении давления. Упругие свойства газа зависят от температуры. При быстром сжатии газа выделяется тепло, которое не успевает распространиться на соседние объемы. Сжатие газа без отвода тепла называется адиабатическим. Адиабатический процесс в газе описывается уравнением Пуассона, а именно:
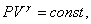
где 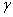 - коэффициент Пуассона. - коэффициент Пуассона.
Так как плотности обратно пропорциональны объемам, то:
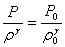 . (2) . (2)
Дифференцируя выражение (2), находим:
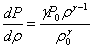 . .
В случае малых сжатий 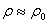 то: то:
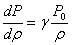 . (3) . (3)
При этом скорость распространения импульсов сжатия (см. (1) и (3))
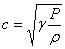 . (4) . (4)
Из уравнения Менделеева-Клапейрона 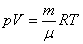 следует, что следует, что 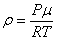 и соотношение (4) можно представить так: и соотношение (4) можно представить так:
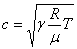 . (5) . (5)
Значит скорость распространения импульса сжатия (звука) растет пропорционально корню квадратному из температуры.
Звуковые волны можно рассматривать как ряд малых импульсов сжатия, следующих вплотную друг за другом и распространяющихся с одинаковой скоростью. Пусть звук распространяется в трубе, диаметр которой меньше длины волны, но все же не слишком тонкой и обладающей гладкими стенками. При этих условиях стенки не вносят значительного затухания. Они обеспечивают распространение колебаний вдоль трубы. Если в одном конце трубы находится поршень, совершающий гармонические колебания, то по столбу газа, заключенному в трубе, распространяется звуковая волна, которую можно считать плоской. Если второй конец трубы закрыт твердой стенкой, то звуковая волна будет отражаться от этой стенки, причем, фаза волны деформации останется прежней, а фазы волны скорости изменятся на 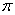 (скорость изменит знак на обратный). (скорость изменит знак на обратный).
При наложении отраженной волны на бегущую может образоваться стоячая волна с распределением смещений y:
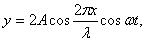 (6) (6)
где
A – амплитуда,
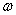 - круговая частота колебаний, - круговая частота колебаний,
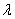 - длина бегущей волны, - длина бегущей волны,
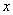 - координата, определяющая положение - координата, определяющая положение
точек среды,
t – время.
Если при отражении не происходит потерь энергии, на закрытом конце трубы всегда образуется узел смещений. Расстояние между соседними узлами или пучностями равно половине длины бегущей волны. Меняя частоту возбуждения, мы будем получать в закрытой трубе стоячие волны всякий раз, когда вдоль трубы будет укладываться целое число полуволн. Скорость звука определится по формуле:
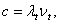 (7) (7)
где
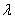 - длина волны, - длина волны,
 - частота собственных колебаний столба воздуха, - частота собственных колебаний столба воздуха,
равная частоте вынужденных колебаний.
Описание устройства
Измерительное устройство (рис.2) состоит из длинной трубы (1), звукового генератора (2), осциллографа (3), термометра или термопары с милливольтметром (4). На концах трубы помещены телефоны (5) и (6), один из которых является передатчиком колебаний, а другой приемником. На трубе сверху помещена обмотка, служащая для увеличения температуры воздуха внутри трубы. Обмотка включается в сеть с напряжением 127 вольт. Силу тока в обмотке можно изменять посредством реостата (7). Телефон (5), во избежание порчи от нагревания, заключен в футляр и омывается проточной водой.
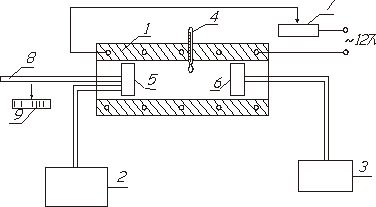
рис.2
Звуковой сигнал генератора вызывает колебания мембраны телефона (6) и подается на осциллограф. Расстояние между телефоном и микрофоном можно изменять посредством рукоятки (8). При этом указатель рукоятки передвигается вдоль шкалы линейки (9).
Выполнение работы
- Осторожно открывают водяной кран, питающий охлаждение телефона (5). (На рисунке не показан).
- Включают питание генератора и осциллографа от сети переменного тока; ждут прогрева – около 5 минут и настраивают приборы. Манипуляции 1 и 2 производит преподаватель или лаборант.
- При заданной частоте генератора медленно двигают рукоятку (8). При этом на экране осциллографа происходит изменение амплитуды колебаний. Записывают все те N положения указателя рукоятки (8), при которых наблюдается максимум амплитуды колебаний. Среднее расстояние между двумя соседними положениями указателя есть
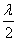 . .
Включают нагреватель и операцию «3» повторяют через интервал температуры 9-12 градусов, повышая температуру до 110-120 градусов Цельсия. Во время каждых измерений, температуру воздуха в трубе поддерживают по возможности постоянной. Для этого в электрическую цепь нагревателя вводят реостат. Так как во время опыта температура будет немного меняться, ее измеряют в начале и в конце опыта и берут среднее значение.
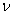
(Гц) |
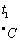
|
N1
см |
N2
см |
N3
см |
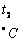
|
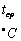
|
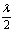
|
CT
см/с |
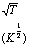
|
|
|
|
|
|
|
|
|
|
|
- По формуле (7) вычисляют скорость звука.
- Строят график зависимости
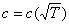 , где T – температура взята по шкале Кельвина. , где T – температура взята по шкале Кельвина.
- Вычисляют коэффициент Пуассона по формуле (5).
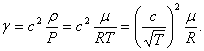 Отношение Отношение 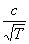 берут из графика берут из графика 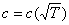 . .
|

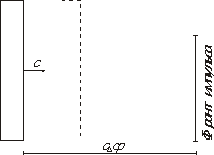
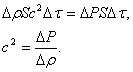 (1)
(1)
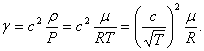 Отношение
Отношение 








