Булева функция
Булева функция ( функция алгебры логики, логическая функция ) - в дискретной математике отображения B N -> B, где B = {0,1} - булева множество. B N - множество всех возможных последовательностей из 0 и 1 длины n. Булева функция задается в виде таблицы, или графика со стандартным ( лексикографическим ) расположением наборов аргументов. В стандартном расположении наборы можно рассматривать как двоичные записи целых чисел от 0 до 2 n - 1. Функцию, заданную со стандартным расположением наборов, можно отождествить с набором длины 2 n. Очевидно, что множество всех возможных наборов длины 2 n, то есть множество n-арних булевых функций, состоит из Нуль-Арним булевыми функциями являются стали 0 и 1. Функции 0 и 1 называются тождественными нулем и единицей, функция x - тождественной, Представим также некоторые из 16 бинарных функций вместе с их обозначениями: Функция, обозначенная выражением, называется конъюнкцией и обозначается еще как x & y, Заметим, что инфиксни обозначения приведенных функций вида xfy, где f - соответствующий знак, сложились исторически. Их так же можно отмечать и в виде f (x, y), например,. |
|
Базисный минор матрицы. Ранг матрицы Алгебраическое дополнение матрицы Вернуться в оглавление: Высшая математика |

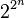 элементов. При n = 0 это 2, при n = 1 - 4, при n = 2 - 16, при n = 3 - 256 т..
элементов. При n = 0 это 2, при n = 1 - 4, при n = 2 - 16, при n = 3 - 256 т.. - отрицанием. Вместо выражения
- отрицанием. Вместо выражения  или xy. Все эти выражения читаются как «x и y».
или xy. Все эти выражения читаются как «x и y».








