Предыдущая формула, полученная в интерпретаторе TeX,
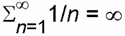
может быть выведена следующим образом (во всех примерах используется figure для создания нового графического окна, поскольку, если оси существуют, то низкоуровневая функция text выводит новый текстовый объект на них, не удаляя имеющиеся на них графические объекты, что приводит к наложению объектов):
figuretext('Position', [0.5 0.5], 'Interpreter', 'latex', 'String',... '$$\sum_{n=1}^\infty\frac1n=\infty$$', 'FontSize', 30)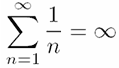
В этом примере использованы следующие команды:
- команда \sum для вывода знака суммирования, в которой верхний и нижний пределы суммирования указываются при помощи знаков верхнего и нижнего индексов (^ и _);
- команда \frac для получения дроби.
Если числитель и знаменатель дроби содержат больше одного символа (или числитель не цифра), то их следует заключать в фигурные скобки. В дальнейшем, для избежания путаницы, будем всегда использовать фигурные скобки, т.е. например вместо \frac12 будем писать \frac{1}{2}. Последовательность команд:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$F(x)=\frac{1+x}{1+\frac{1+x^2}{1+x^3}}$$','FontSize', 20)приводит к формуле
|
|
|
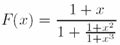
в которой символы x и цифры имеют разные размеры в зависимости от того, в какой из дробей они находятся.
Для того, чтобы размер символов в дроби 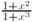 , стоящей в знаменателе в предыдущей формуле, совпадал с размером остальных символов в этой формуле, следует использовать команду \displaystyle, помещаемую перед командой \frac, как это сделано в следующем примере
, стоящей в знаменателе в предыдущей формуле, совпадал с размером остальных символов в этой формуле, следует использовать команду \displaystyle, помещаемую перед командой \frac, как это сделано в следующем примере
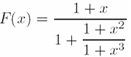
Для написания интегралов используется команда \int, однако указание пределов при помощи знаков _ и ^ приводит к тому, что пределы расположены не сверху и снизу от знака интеграла (как для суммы), а правее него:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\frac{1}{b^a\Gamma(a)}\int_{0}^{x}t^{a-1}e^{\frac{t}{b}} dt$$','FontSize', 20)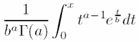
Если же требуется расположить верхний и нижний пределы интегрирования строго сверху и снизу по отношению к знаку интеграла, то необходимо добавить команду \limits сразу после команды \int, например:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\frac{1}{b^a\Gamma(a)}\int\limits_{0}^{x}t^{a-1}e^{\frac{t}{b}} dt$$','FontSize', 20)делает формулу, которая занимает немного больше места по вертикали, по сравнению с предыдущей, но выглядит несколько красивее:
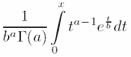
Кроме обычного знака интеграла есть еще знак для контурного интеграла, который выводится при помощи команды \oint, например:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\oint_{\Gamma} f(s) ds$$', 'FontSize', 30)выводит интеграл по контуру:
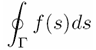
Разумеется, для того, чтобы символ Г находился снизу, а не справа от знака интеграла, следует сразу после \oint применить команду \limits, как и в предыдущем примере.
|
|
|
В отличие от интегралов, пределы суммирования по умолчанию указываются над и под знаком суммы. Если же требуется расположить их справа от знака суммирования, то следует указать команду \nolimits, например:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\sum\nolimits_{n=1}^\infty\frac1n=\infty$$', 'FontSize', 20)обеспечивает требуемый результат
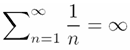
Для вывода знака предела применяется команда \lim, которая позволяет задать подпись под ней при помощи знака нижнего индекса:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\lim_{x\rightarrow0} \frac{\sin x}{x}=1$$', 'FontSize', 20)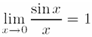
Команды для других символов, допускающих задание пределов, примеры их использования и получающийся результат приведены в следующей таблице.
| Команда | Пример | Результат |
| \min | '$$\min_{x\in[a,b]}f(x)$$' | 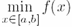
|
| \max | '$$\max_{x\in[a,b]}f(x)$$' | 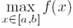
|
| \inf | '$$\inf_{x\in[a,b]}f(x)$$' | 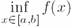
|
| \sup | '$$\sup_{x\in[a,b]}f(x)$$' | 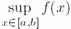
|
| \bigcup | '$$\bigcup_{i=1}^{n+1}A_{i}$$' | 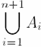
|
| \bigcap | '$$\bigcap_{i=1}^{n+1}B_{i}$$' | 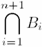
|
| \bigoplus | '$$\bigoplus_{k=1}^{\infty}\tau^{(k)}$$' | 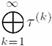
|
| \bigotimes | '$$\bigotimes_{k\ne i}\Delta^k$$' | 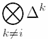
|
Знак квадратного корня выводится при помощи команды \sqrt, а само подкоренное выражение заключается в фигурные скобки, например:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\sqrt{1+\sqrt{1+x}}$$', 'FontSize', 20)создает выражение, в которое входят квадратные корни
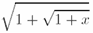
Если же требуется получить корень заданной степени, то значение степени указывается в квадратных скобках после команды \sqrt, а уже после нее идет подкоренное выражение, взятое в фигурные скобки, например:
figuretext('Position', [0.1 0.5], 'Interpreter', 'latex', 'String',... '$$\sqrt[3]{1+\sqrt[7]{1+x}}$$', 'FontSize', 20)приводит к
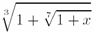
 2015-05-29
2015-05-29 497
497








