(a + i b) n = (r (cos (φ)+ i·sin (φ))) n = rn (cos (nφ)+ i·sin (nφ))
5. Извлечение корня n-ой степени
Для извлечения корня n-й степени (n > 1, n I Z) из комплексного числа 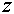 в тригонометрической форме используется формула, дающая n значений этого корня
в тригонометрической форме используется формула, дающая n значений этого корня
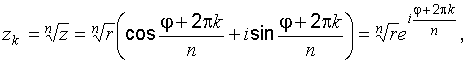
Где 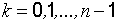
6. Разложение многочлена на множители
Раскладывать многочлены на множители приходится при упрощении выражений (чтобы можно было провести сокращение), при решении уравнений или при разложении дробно рациональной функции на простейшие дроби
При делении многочлена 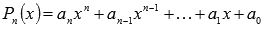 на (x- s) получается остаток, равный значению многочлена в точке s, то есть
на (x- s) получается остаток, равный значению многочлена в точке s, то есть
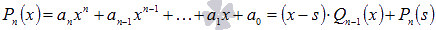 , где
, где 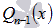 есть многочлен степени n – 1
есть многочлен степени n – 1
При делении многочлена f(x) на разность x – a получается остаток, равный f(a).
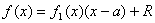 , где R - остаток
, где R - остаток
Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
7. Понятие множества. Операции над множествами.
Множество - это совокупность, набор элементов, объединенных общими свойствами. Обозначаются заглавными латинскими буквами 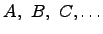 , а элементы множества строчными латинскими буквами
, а элементы множества строчными латинскими буквами 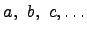 .
.
Основные операции:
а) Принадлежность элемента множеству:
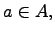
б) Непринадлежность элемента множеству:
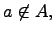
в) Объединение множеств:
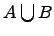
г) Пересечение множеств:
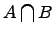
д) Разность множеств:
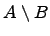
е) Симметрическая разность множеств:
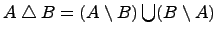
ж) Дополнение множества:
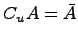
з) Вхождение одного множества в другое множество:
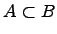
и) Не вхождение одного множества в другое множество:
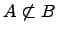
8. Функциональная зависимость.
а) Пропорциональные величины y = k x,
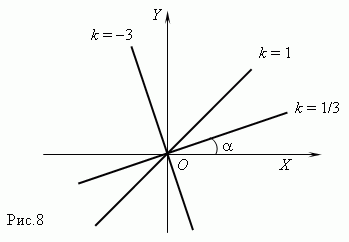
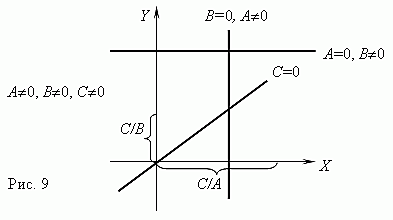
б) Линейная функция A x + B y = C,
в) Обратная пропорциональность y = 
 Основные характеристики и свойства гиперболы:
Основные характеристики и свойства гиперболы:
- область определения функции: x  0, область значений: y
0, область значений: y  0;
0;
- функция монотонная (убывающая) при x < 0и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?);
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
г) Квадратичная функция y = ax 2 + bx + c
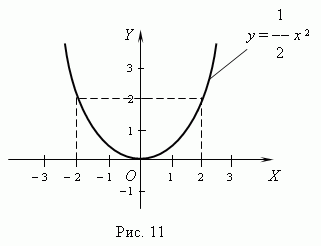 Основные характеристики и свойства квадратной параболы:
Основные характеристики и свойства квадратной параболы:
- область определения функции: - 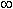 < x < +
< x < + 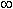 (т.e. x
(т.e. x 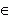 R), а область
R), а область
значений: … (ответьте, пожалуйста, на этот вопрос сами!);
- функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0,
и непериодическая;
- при D < 0 не имеет нулей. (А что при D  0?)
0?)
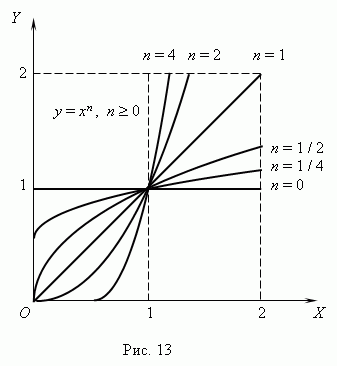
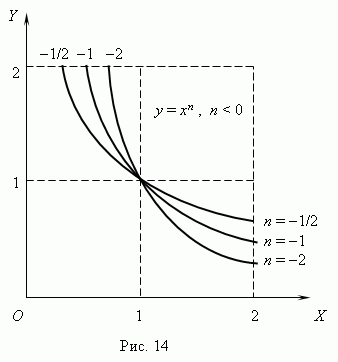
д) Степенная функция y = axn
е) Показательная функция y = ax
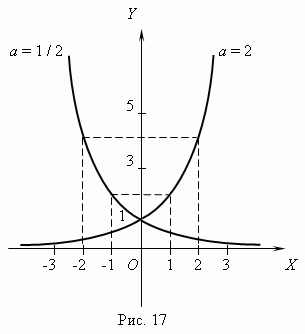 Основные характеристики и свойства показательной функции:
Основные характеристики и свойства показательной функции:
- область определения функции: - 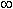 < x < +
< x < + 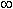 (т.e. x
(т.e. x 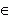 R);
R);
область значений: y > 0;
- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.
ж) Логарифмическая функция y = log a x
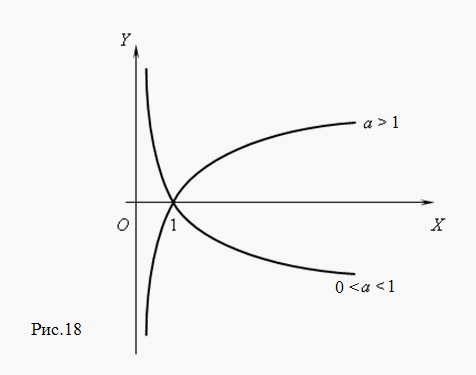
Основные характеристики и свойства логарифмической функции:
- область определения функции: x > 0,а область значений: - 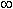 < y < +
< y < + 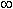
(т.e. y 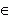 R);
R);
- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
з) Тригонометрическая функция
y = sin x
y = cos x
Характеристики и свойства этих функций:
- область определения: - 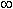 < x < +
< x < + 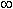 ;область значений: -1
;область значений: -1 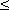 y
y 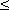 +1;
+1;
- эти функции периодические: их период 2  ;
;
- функции ограниченные (| y | 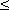 1), всюду непрерывные, не монотонные, но
1), всюду непрерывные, не монотонные, но
имеющие так называемые интервалы монотонности, внутри которых они
ведут себя, как монотонные функции (см. графики рис.19 и рис.20);
- функции имеют бесчисленное множество нулей
y = tg x
y = ctg x
и) Обратные тригонометрические функции
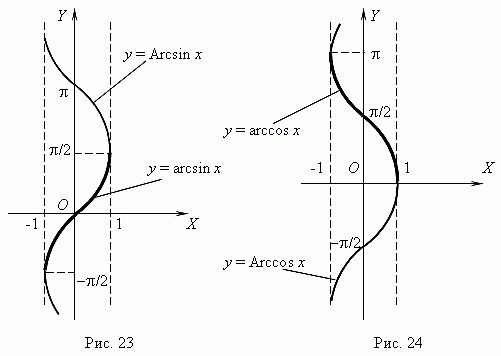
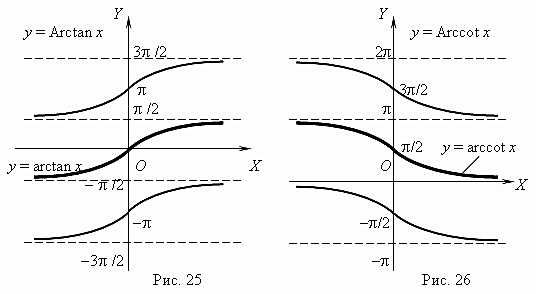
9. Числовая последовательность.
Числовая последовательность — это последовательность элементов числового пространства.
Пусть на множестве x определена N- арная операция f
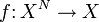
Тогда для элементов 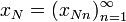 множества всех последовательностей элементов множества x операция f будет определяться следующим образом:
множества всех последовательностей элементов множества x операция f будет определяться следующим образом:
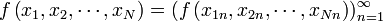
Суммой числовых последовательностей 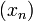 и
и 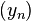 называется числовая последовательность
называется числовая последовательность 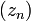 такая, что
такая, что 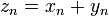
Разностью числовых последовательностей 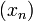 и
и 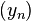 называется числовая последовательность
называется числовая последовательность 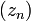 такая, что
такая, что 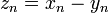
Произведением числовых последовательностей 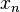 и
и 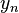 называется числовая последовательность
называется числовая последовательность 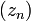 такая, что
такая, что 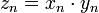
Частным числовой последовательности 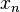 и
и 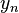 , все элементы которой отличны от нуля, называется числовая последовательность
, все элементы которой отличны от нуля, называется числовая последовательность
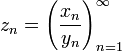
Основные теоремы:
а) Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
б) Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
в) Бесконечно малая последовательность ограничена.
г) Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
д) Если элементы бесконечно малой последовательности 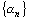 равны одному и тому же числу С, то С =0.
равны одному и тому же числу С, то С =0.
е) Если 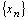 – бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность
– бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность 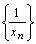 , которая является бесконечно малой. Если не все элементы бесконечно малой последовательности
, которая является бесконечно малой. Если не все элементы бесконечно малой последовательности 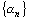 равны нулю, то последовательность
равны нулю, то последовательность 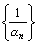 бесконечно большая.
бесконечно большая.
10. Ограниченные и неограниченные последовательности.
· Ограниченная сверху последовательность — это последовательность элементов множества 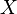 , все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
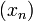 ограниченная сверху
ограниченная сверху 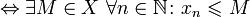
· Ограниченная снизу последовательность — это последовательность элементов множества 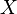 , для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
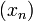 ограниченная снизу
ограниченная снизу 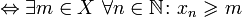
· Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.
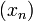 ограниченная
ограниченная 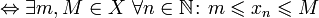
· Неограниченная последовательность — это последовательность, которая не является ограниченной.
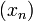 неограниченная
неограниченная 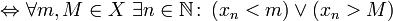
Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.
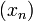 ограниченная
ограниченная 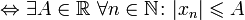
 2015-05-30
2015-05-30 858
858








