Число групп (интервалов) приближенно определяется по формуле Стерджесса:
m = 1 + 3,322 × lg(n)
где n - общее число единиц наблюдения (общее количество элементов в совокупности и т.д.), lg(n) – десятичный логарифм от n.
Полученную по формуле Стерджесса величину округляют обычно до целого большего числа, поскольку количество групп не может быть дробным числом.
Если ряд интервальный ряд с таким количеством групп по каким-то критериям не устраивает, то можно построить другой интервальный ряд, округлив m до целого меньшего числа и выбрать из двух рядов более подходящий.
Число групп не должно быть больше 15.
Также можно пользоваться следующей таблицей, если совсем нет возможности вычислить десятичный логарифм.
| Объем выборки, n | 25-40 | 40-60 | 60-100 | 100-200 | Больше 200 |
| Число интервалов, m | 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
2. Определяем ширину интервала
Ширина интервала для интервального вариационного ряда с равными интервалами определяется по формуле:
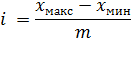
где Xмакс - максимальное из значений xi, Xмин - минимальное из значений xi; m - число групп (интервалов).
Величину интервала ( i ) обычно округляют до целого числа, исключение составляют лишь случаи, когда изучаются малейшие колебания признака (например, при группировке деталей по величине размера отклонений от номинала, измеряемого в долях миллиметра).
Часто применяется следующее правило:
| Количество знаков до запятой | Количество знаков после запятой | Пример ширины интервала по формуле | До какого знака округляем | Пример округленной ширины интервала |
| 0,375 | 0,01 | 0,38 | ||
| 0,56 | 0,1 | 0,6 | ||
| 4,658 | 0,01 | 4,66 | ||
| 2,54 | 0,1 | 2,5 | ||
| любое | 12,54 | 1,0 | ||
| любое | 672,54 | 10,00 | ||
| любое | 3472,45 | 100,00 | ||
| и т.д. |
 2015-05-30
2015-05-30 38569
38569








