1. Введение. 3
2. Сплайны, простейшие свойства. 4
3. Использование сплайнов в графических средах. 8
3.1 Графика в Maple. 9
3.2 Примеры построения графиков сплайнов в Maple. 13
3.3 Графика в Autodesk 3ds Max. 16
4. Сплайны в 3ds Max. 18
4.1 Основы моделирования. Создание моделей с помощью сплайнов. 18
4.2 Создание трехмерных объектов методом лофтинга. 28
5. Практическая работа. Создание модели корпуса автомобиля при помощи сплайнов в 3Ds Max. 36
Литература и источники. 56
1. Введение
В дипломной работе рассматривается один из мощных инструментов, используемых в векторной графике – сплайны. Сплайны первоначально использовались для решения прикладных математических задач, в том числе интерполяции, нахождении наилучшей квадратурной формулы и т.д. в настоящее время теория сплайнов получила большое использование в моделировании и компьютерной графике.
Векторная графика получила большую популярность и широкое распространение. В мире множество программ для моделирования в различных сферах, наиболее известные - Maya, ArchiCad, 3 D’S MAX. В каждой из них используются сплайны.
Сплайн - основное понятие всей векторной графики. Суть сплайна: любую элементарную кривую можно построить по четырем точкам на плоскости. Перемещая эти точки, меняем кривую.
В данной работе рассмотрено использование сплайнов в моделировании, а именно в программе 3ds Max. Итогом является практическая работа: создание модели корпуса автомобиля BMW X5, при построении которого в качестве основного инструмента использовались простые виды сплайна.
Во втором пункте работы приведено определение сплайна и простейшие свойства. В третьем - представлено использование сплайнов в Maple и в 3ds Max. Приведены примеры.
В четвертом пункте подробно рассматривается использование сплайнов в 3ds Max, а также модификаторы для данного инструмента, необходимые для 3х-мерного моделирования. В пятом - приведена практическая часть, в которой рассматриваются этапы создания модели автомобиля BMW X5.
2. Сплайны, простейшие свойства.
В этом пункте вводится понятие полиномиального сплайна, приведены его простейшие свойства, рассмотрена задача кратной сплайн-интерполяции и условия ее однозначной разрешимости, а также оценка погрешности.
«Сплайн» (англ. spline) в переводе означает лекало (гибкую линейку) для проведения гладких кривых через заданные точки плоскости.
Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную в R1 и имеющую некоторое число непрерывных производных.
Основная область применения сплайнов – задачи интерполяции. Преимуществом сплайнов перед обычной интерполяцией является их сходимость и устойчивость процесса вычислений и возможность иметь нуль-интервалы.
2.1 Определение сплайна и его простейшие свойства.
Пусть r, m- натуральные числа.
Определение. Полиномиальным сплайном степени r с m узлами 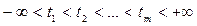 называется кусочно-полиномиальная функция, которая на каждом из своих частичных промежутков (-∞,
называется кусочно-полиномиальная функция, которая на каждом из своих частичных промежутков (-∞, 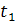 ], [
], [ 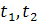 ],…[
],…[ 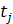 ,+∞) представляет собой полином степени не выше, чем r и всюду r-1 раз непрерывно дифференцируема, т.е.
,+∞) представляет собой полином степени не выше, чем r и всюду r-1 раз непрерывно дифференцируема, т.е. 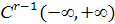
Заметим, что при r=1 сплайн первой степени представляет из себя непрерывную ломаную.
Сплайны очень удобно применять для решения задач интерполяции. Отличительные особенности сплайнов от полиномиального случая заключаются в следующем:
1. наличие 2 систем узлов: 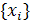 - узлы интерполяции и
- узлы интерполяции и 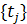 - узлы сплайна;
- узлы сплайна;
2. сплайн может обращаться в нуль на целых интервалах, что невозможно для полиномов;
3. условие однозначной разрешимости задачи сплайн-интерполяции будет зависеть от взаимного расположения узлов сплайна и узлов интерполяции.
Пусть r 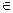 N.
N.
Определение. Функцией срезки 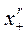 назовем следующую функцию
назовем следующую функцию
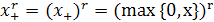 .
.
Заметим, что
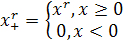
Отметим некоторые свойства функции срезки.
1. Для k∈1: (r-1) производная функции срезки вычисляется по формуле
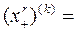
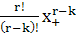
2. При x≠0 производная r -го порядка
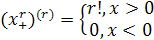 .
.
Заметим, что в точке х=0 эта производная терпит разрыв 1-го рода, а значит r- ая производная функции срезки не является непрерывной, поэтому 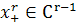
Отметим, что функция 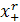 - функция, r-ая производная которой в точке х=0 имеет конечный скачок.
- функция, r-ая производная которой в точке х=0 имеет конечный скачок.
Определение. Функция вида
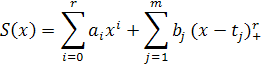
называется полиномиальным сплайном степени r с m узлами
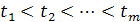 .
.
Заметим, что это определение эквивалентно приведенному выше, так как:
1. S(x) 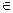
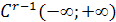 . Это следует из свойств функции срезки.
. Это следует из свойств функции срезки.
2. нетрудно видеть, что на каждом из частичных промежутков (-∞, 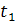 ], [
], [ 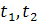 ],…[
],…[ 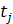 ,+∞) функция S(x) представляет собой полином степени не выше, чем r (причем эти полиномы могут быть, вообще говоря, различными на различных промежутках).
,+∞) функция S(x) представляет собой полином степени не выше, чем r (причем эти полиномы могут быть, вообще говоря, различными на различных промежутках).
2.2. ЗАДАЧА КРАТНОЙ СПЛАЙН-ИНТЕРПОЛЯЦИИ
Рассмотрим задачу кратной интерполяции при помощи полиномиальных сплайнов класса (r,m) с фиксированными узлами
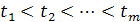 .
.
Пусть S(x) 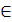 S(r,m) – полиномиальный сплайн степени r с m узлами
S(r,m) – полиномиальный сплайн степени r с m узлами
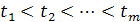 .
.
Пусть x1, x2, …, xp - узлы интерполяции, имеющие соответственно кратности σ1, σ2, …, σp
Рассмотрим задачу кратной сплайн-интерполяции в следующей постановке:
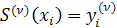 ,
, 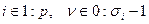 . (3.1)
. (3.1)
Пусть n=r+1+m, 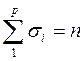 ,
, 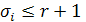 и
и 
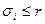 , если
, если 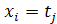 .
.
Отметим некоторые свойства задачи (3.1) [4].
Обозначим через V(ti,tj) – количество узлов интерполяции с учетом их кратности, попадающие в замыкание отрезка  (ti,tj), где t0=-
(ti,tj), где t0=- 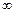 , tm+1=+
, tm+1=+ 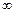 .
.
Теорема. Для того, чтобы задача (3.1) при любых 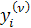 имела единственное решение, необходимо и достаточно, чтобы
имела единственное решение, необходимо и достаточно, чтобы
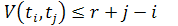
при всех 0 ≤ i < j ≤ m+1.
Обозначим через 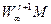 - класс функций f, имеющий на [c,d] абсолютно непрерывную r -ю производную и почти всюду (r+1) производную, такую, что
- класс функций f, имеющий на [c,d] абсолютно непрерывную r -ю производную и почти всюду (r+1) производную, такую, что
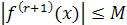 .
.
Оценку погрешности для задачи (1) на всем классе функций 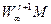 дает следующее утверждение
дает следующее утверждение
Теорема. Существует единственная функция вида
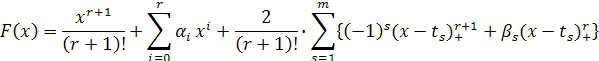
удовлетворяющая условиям
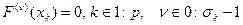 .
.
Тогда для любой 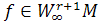 справедлива оценка
справедлива оценка
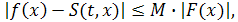
 2015-05-30
2015-05-30 915
915








