Подмножество. Основные числовые множества

Нередко одно множество является частью другого множества. Например: множество всех женщин составляет часть множества всех людей; множество четных чисел – часть множества целых чисел. Для описания этой ситуации используется термин «подмножество».

Опр. 2.2.1. Множество А, состоящее из некоторых элементов данного множества В (и только из них), называется подмножеством (частью) этого множества. Иначе, если любой элемент множества А принадлежит также множеству В, то множество А называется подмножеством множества В.

Это записывается так: АÌ В или ВÌ А. Говорят, что «А – подмножество В» или «А содержится в В» или «В содержит А». Заметим, что m (А) ≤ m (В).

Если в множестве А найдется хотя бы один элемент, не принадлежащий множеству В, то А не является подмножеством множества В.

Из опр.2.2.1. следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение АÌ А. Полагают также, что пустое множество является подмножеством любого множества. Пустое множество не содержит ни одного элемента, а значит, в нем нет элемента, не принадлежащего любому другому множеству.

Исключив эти «крайние» случаи (т.е. Æ, A), мы получим, так называемые, собственные подмножества множества A, т.е. такие, которые не пусты и не совпадают с A.

Примеры. 1)Если А={а₁, а₂, а₃}, то оно имеет следующие подмножества: Æ, {а₁}, {а₂}, {а₃}, {а₁, а₂}, {а₁, а₃}, {а₂, а₃}, {а₁, а₂, а₃}. Всего 8 подмножеств.

2) Если А — множество линий на плоскости, В — множество прямых на плоскости, то В Ì А.

3) N Ì Z Ì Q Ì R. (Множество натуральных чисел является подмножеством множества целых чисел, которое входит во множество рациональных чисел, которое, в свою очередь, содержится во множестве действительных чисел).

4) Многие теоремы в математике имеют вид: A Ì B. Например, в теореме «Диагонали ромба взаимно перпендикулярны» речь идет о двух множествах: A – множество всех ромбов, B – множество всех геометрических фигур с перпендикулярными диагоналями. И теорема состоит в том, что A Ì B.

5) Отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. аÎ [а, b], но а Ï (а, b].

Знак Ì называется знаком включения. Отметим основные свойства отношения включения между множествами:

1) ØÌ А для любого множества А;

2) АÌ А для любого множества А (рефлексивность);

3) из того, что ВÌ А не следует АÌ В (не симметричность);

4) если АÌ В и ВÌ А, то А=В (антисимметричность);

5) если АÌ В и ВÌ С, то АÌ С (транзитивность).

Основные числовые множества:

N ={1,2,3,4,…} – множество натуральных чисел;

Z ={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все

натуральные числа и числа, им противоположные);

Q ={ x | x=p/q, где p Ì Z, q Ì N } – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби);

R =(-∞;+∞) – множество действительных чисел, QÌR (кроме всех рациональных чисел, содержит иррациональные числа, содержащие в своей записи знаки радикалов: ).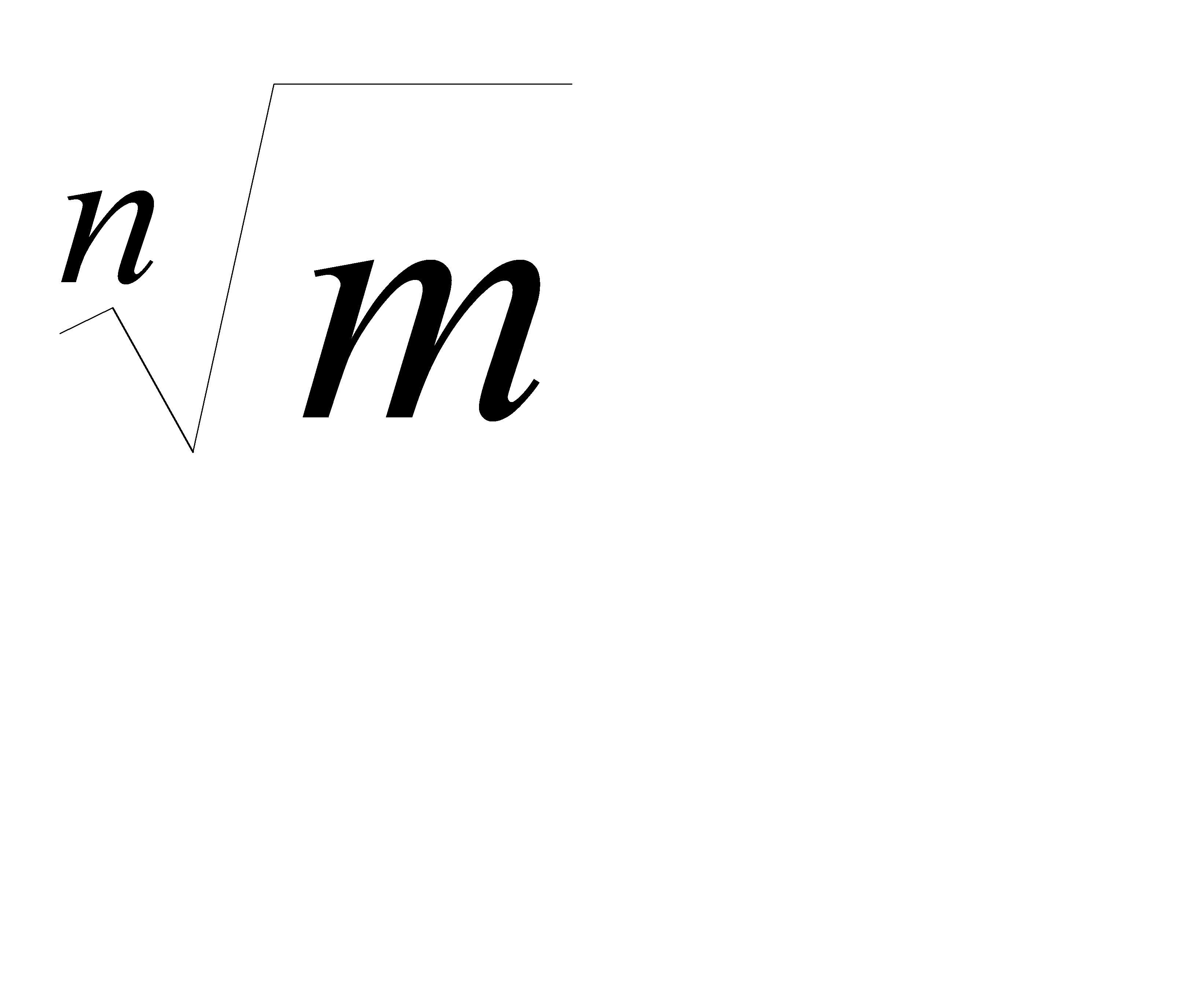

Действительные числа изображаются точками координатной прямой (числовой оси). Координатная прямая – это всякая прямая (обычно горизонтальная), на которой указаны положительное направление, начало отсчета и единичный отрезок.