Свойства счетных множеств

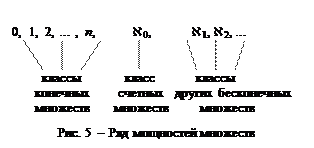
Класс счетных множеств расположен в ряду мощностей левее любых других классов бесконечных множеств, а предшествуют ему только классы конечных множеств (рис. 5).

Основой для такого утверждения служат следующие теоремы, доказательства которых демонстрируют методы решения задач о счетных множествах.

Теорема 1. Любое подмножество счетного множества конечно или счетно.

Пусть X – счетное множество, а 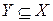– произвольное его подмножество. Занумеруем элементы множества 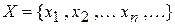и выберем тот элемент, который имеет минимальный номер и принадлежит подмножеству Y, – обозначим его 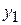. Затем рассмотрим множество 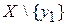и найдем в нем элемент с минимальным номером, принадлежащий Y, – обозначим 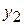, и т.д. Если на n -ом шаге мы не обнаружим в множестве 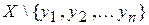элементов множества Y, то Y конечно и ½ Y ½= n. В противном случае (если процесс будет продолжаться бесконечно) множество Y счетное, т.к. указан способ нумерации его элементов.

Теорема 2. Всякое бесконечное множество имеет счетное подмножество.

Пусть X – бесконечное множество. Выберем произвольный элемент 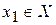. Так как X бесконечно, то 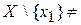Æ. Обозначим 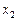произвольный элемент из 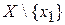. Далее найдется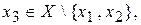 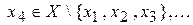. Поскольку X бесконечно, этот процесс не может оборваться из-за «нехватки» элементов, и мы получим счетное подмножество Y множества X: .

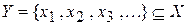Теорема 3. Объединение конечного или счетного количества счетных множеств есть множество счетное.

Пусть , где 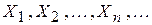– счетные множества. Будем считать, что они попарно не пересекаются (в противном случае перейдем от множеств 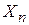к множествам 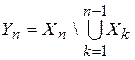, которые попарно не пересекаются и 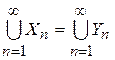). Все элементы множества X запишем в виде бесконечной матрицы:

,

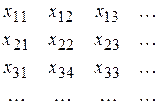где в первой строке записаны элементы множества 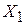, во второй – 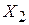и т.д. Занумеруем эти элементы «по диагонали»(как в примере 2 из 1.4.5), при этом устанавливается биекция между множествами X и N, т.е. X – счетное множество.

Теорема 4. Пусть X бесконечное множество, а Y – счетное. Тогда .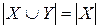

Теорема утверждает, что добавление счетного множества элементов не увеличивает мощность бесконечного множества.

Доказательство. Рассмотрим множество 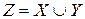и представим его в виде объединения непересекающихся множеств 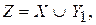где 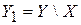. Так как Y счетно, то 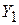конечно или счетно (по теореме 1). Множество X бесконечно, значит, существует счетное подмножество 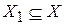(по теореме 2). Тогда , а 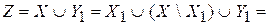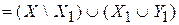.По теореме 3 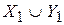счетно, т.е. 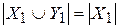. Поэтому 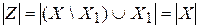. Теорема доказана.

В примере 1 из 1.4.5 мы установили, что множество N равномощно своему собственному подмножеству. Рассуждения, аналогичные доказательству теоремы 4, позволяют утверждать, что таким свойством обладает не только множество N, но любые бесконечные множества.

Рассмотренные четыре теоремы показывают, что среди бесконечных множеств счетные множества являются наименьшими по мощности. Существуют ли множества более чем счетные?