Пусть известна ПР СДСВ. Используя формулу (4) представим ФР составляющих  и
и 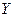 в виде:
в виде:
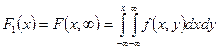 ;
;
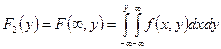 .
.
Дифференцируя равенства по соответствующим переменным, получим выражения для плотностей распределения составляющих:
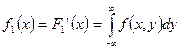 ;
;
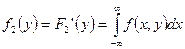 .
.
Таким образом, чтобы получить ПР одной из величин, входящих в систему, нужно ПР системы проинтегрировать в бесконечных пределах по аргументу, соответствующему другой СВ.
Обратная задача: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Если СВ  и
и 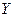 зависимы между собой, то закон распределения системы не может быть выражен через законы распределения составляющих. Это приводит к необходимости введения условных законов распределения.
зависимы между собой, то закон распределения системы не может быть выражен через законы распределения составляющих. Это приводит к необходимости введения условных законов распределения.
Опр. Распределение одной СВ, входящей в систему, найденное при условии, что другая СВ,, входящая в систему, приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как ФР, так и ПР. Условная ФР - 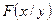 , условная ПР -
, условная ПР - 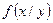 .
.
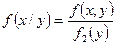 (5)
(5)
- ПР величины  , при условии, что величина
, при условии, что величина 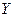 приняла определенное значение. Аналогично
приняла определенное значение. Аналогично
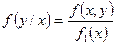 (6)
(6)
- ПР величины 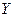 , при условии, что величина
, при условии, что величина  приняла определенное значение.
приняла определенное значение.
Из соотношений (5) и (6) следует, что
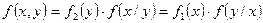 . (7)
. (7)
Равенство (7) называют теоремой умножения законов распределения.
Условная ПР обладает всеми свойствами безусловной ПР. В частности,
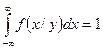 ,
, 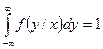 .
.
Для краткого описания условных законов распределения мы можем использовать различные характеристики, например, условное МО (УМО):
Опр. УМО ДСВ  , при условии, что величина
, при условии, что величина 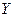 приняла определенное значение
приняла определенное значение 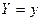 , называется сумма возможных значений
, называется сумма возможных значений  на их условные вероятности:
на их условные вероятности:
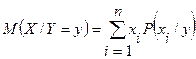 .
.
Для НСВ:
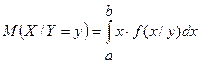 ,
,
где 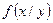 - условная ПР величины
- условная ПР величины  при
при 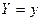 .
.
Аналогично, УМО ДСВ 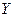 , при условии, что величина
, при условии, что величина  приняла определенное значение
приняла определенное значение 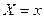 , называется сумма возможных значений
, называется сумма возможных значений 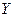 на их условные вероятности:
на их условные вероятности:
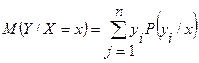 .
.
Для НСВ:
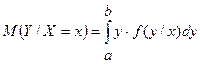 ,
,
где 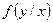 - условная ПР величины
- условная ПР величины 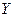 при
при 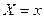 .
.
Из определения УМО 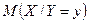 следует, что с изменением значения
следует, что с изменением значения 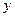 будет меняться и
будет меняться и 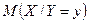 . Это значит, что мы можем рассматривать функцию
. Это значит, что мы можем рассматривать функцию 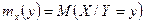 , областью определения которой является множество возможных значений СВ
, областью определения которой является множество возможных значений СВ 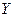 . Эта функция носит название регрессии
. Эта функция носит название регрессии  по
по 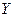 .
.
Аналогично, УМО 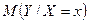 является функцией
является функцией 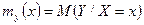 , которая носит название регрессии
, которая носит название регрессии 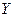 по
по  .
.
Уравнения
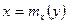 и
и 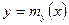 (8)
(8)
называются уравнениями регрессии соответственно по  по
по 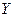 и
и 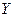 по
по  . Линии, определяемые уравнениями (8), называются линиями регрессии. Эти линии вводятся лишь для НСВ (для ДСВ эти «линии» будут состоять из изолированных точек плоскости).
. Линии, определяемые уравнениями (8), называются линиями регрессии. Эти линии вводятся лишь для НСВ (для ДСВ эти «линии» будут состоять из изолированных точек плоскости).
 2015-06-10
2015-06-10 568
568








