Множества. Операции над множествами

Множеством называется совокупность некоторых предметов, объединенных общим признаком. Элементы множества – это те предметы, из которых состоит множество.

Если какой-то элемент а принадлежит множеству А, то это обозначается аÎА, а если b не принадлежит А, то – bÏА. Например, пусть А – множество четных натуральных чисел, тогда 6ÎА, а 3ÏА.

Пусть имеется два множества А и В, причем все элементы множества А принадлежат множеству В, т.е. если хÎА, то хÎB. В этом случае говорят, что множество А включено в множество В. Обозначается: АÍВ (Í – символ нестрогого включения, т.е. возможно совпадение множеств). Множество А совпадает с множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А. Это можно записать в виде

(АÍВ и ВÍА) Û (А = В).

Большинство утверждений теории множеств связано с равенством двух множеств и включением одного множества в другое. Поэтому надо детально разобраться в методах доказательства этих фактов.

1. Доказательство включения АÍВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е.

(" x Î А) Þ (x Î В).

2. Доказательство равенства А = В. Оно сводится к доказательству двух включений А Í В и В Í А.

Определим следующие операции над множествами.

1. Объединение. Пусть А и В – произвольные множества. Их объединением называется множество С = А È В, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В.

2. Пересечение. Пересечением множеств А и В называется множество С, состоящее из элементов, одновременно принадлежащих А и В. Обозначается так: C = A Ç B.

3. Разность. Разность множеств А и В – это множество С (С = А \ В), состоящее из элементов множества А, не принадлежащих множеству В. Если В Í А, то разность С = А \ В называется дополнением В до А.

Считается, что все множества включены в некоторое множество U, которое называют универсальным множеством. В этом случае дополнение какого-либо множества А до U обозначается С (А) или .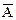

4. Симметричная разность. По определению симметричная разность двух множеств А и В – это множество

С = А D В = (А \ В) È (В \ А).

Задача 1. Доказать, что для любых множеств A₁, A₂,..., A_n если справедливы включения A₁ Í A₂ Í... Í A_n Í A₁, то A₁ = A₂ =... =A_n.

Решение.

Задача 2. Доказать тождество

(AÇB) \ C = (A \ C)Ç(B \ C) = AÇ(B \ C) = (AÇB)\(AÇC).

Решение.

1) Пусть xÎ(AÇB)\C, тогда xÎAÇB и xÏC. Так как x принадлежит пересечению, то он принадлежит каждому из множеств. Следовательно, xÎA и xÏC, что означает xÎA\C. Аналогично из xÎB и xÏC следует, что xÎB\C. Так как x принадлежит обоим множествам, то xÎ(A\C)Ç(B\C). Следовательно, (AÇB)\CÍ (A\C)Ç(B\C).

2) Покажем теперь, что (A\C) Ç (B\C) AÇ (B\C). Так как xÎ(A\C)Ç(B\C), то xÎA\C и xÎB\C, а, следовательно, xÎA, xÎB и xÏC. Поэтому xÎB\C и xÎA, что и означает требуемое.

3) Пусть xÎAÇ(B\C), тогда xÎA, xÎB и xÏC. Следовательно, xÎAÇB и xÏAÇC. Но тогда по определению разности xÎ(AÇB)\(AÇC).

4) Пусть теперь xÎ(AÇB)\(AÇC), покажем, что xÎ(AÇB)\C. Из условия следует, что xÎAÇB и xÏAÇC. Первое свойство означает, что xÎA и xÎB, второе - xÏA или xÏC. Так как при xÏA получим противоречие, то остается лишь случай xÏC. Поэтому имеем xÎA, xÎB и xÏC. Но тогда xÎAÇB и xÏC и, следовательно, xÎ (AÇB)\C.

Таким образом, доказана цепь включений

(AÇB)\C Í (A\C)Ç(B\C) Í AÇ(B\C) Í (AÇB)\(AÇC) Í Í(AÇB)\C.

Для завершения доказательства остается воспользоваться результатами задачи 1.

Задача 3. Доказать тождество

A Ç (B D C) = (A Ç B) D (A Ç C).

Решение. Воспользовавшись свойством дистрибутивности и результатами задачи 2, получим

AÇ(BDD) = AÇ((B\D)È(D\B)) = (AÇ(B\D))È(AÇ(D\B)) =

= ((AÇB)\(AÇD))È((AÇD)\(AÇB)) = (AÇB) D (AÇD).

Задача 4. Доказать, что A Í (B Ç C) Û A Í B и A Í C;

Решение. Докажем, что из AÍ(BÇC) следует AÍB и AÍC. Для этого необходимо показать, что если выполнено включение посылки, т.е. AÍBÇC, то выполняются и оба включения следствия.

Пусть xÎA, тогда по условию xÎBÇC, а, следовательно, xÎB и xÎC. Поэтому справедливы включения AÍB и AÍC.

Докажем обратное следствие. Пусть выполнены оба включения AÍB и AÍC. То есть из xÎA вытекает, что xÎB и xÎC. Но это означает, что xÎBÇC. Следовательно, требуемое включение доказано.

Задача 5. Решить систему уравнений .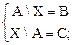

Решение. Так как A\X=B, то BÍA, XÇB=Æ, A\BÍX и AÍXÈB. Выполнение первых двух свойств очевидно.

Докажем справедливость третьего включения. Пусть xÎA\B, тогда xÎA и xÏB. Покажем, что xÎX. Предположим противное, т.е. xÏX, тогда из B=A\X получим xÎB, что противоречит условию. Следовательно, xÎX.

Так как BÍA, то A=(A\B)ÈB. Из этого равенства и условия A\BÍX следует, что AÍXÈB.

Аналогично из X\B=A следует, что CÍX, AÇC=Æ, XÍAÈC и X\CÍA. Так как A\BÍX и CÍX, то (A\B)ÈCÍX. Кроме того, из XÍAÈC, BÍA и XÇB=Æ следует, что XÍ(A\B)ÈC. Поэтому X=(A\B)ÈC, где BÍA и AÇC=Æ.