Состоянием

Подключение дополнительных контуров обратной связи в многоконтурных системах обеспечивает повышение качества управления. Наиболее полная информация об управляемом объекте содержится в переменных состояния. Управление по состоянию предусматривает введение в структуру системы контуров прямых и обратных связей по переменным состояния объекта управления. При этом задача стабилизации и слежения формулируется как задача поддержания постоянного X^* = const или изменяющегося по заданному закону X^* (t) состояния объекта управления X^* = X^* (t).

Изменяющиеся во времени или фиксированные сигналы x_i^* , определяющие требуемый характер изменения переменных состояния x_i , составляют расширенный вектор задания X^* = { x_i^* }, а ошибка движения объекта управления по состоянию определяется вектором отклонения e = X^* - X.

Упраление по состоянию, как и управление по выходу объекта управления, может быть разомкнутым: U = F[X^*], замкнутым U = F[e], или комбинированным: U = F[e, X^*].

Системы с регуляторами состояния относятся к многоконтурным системам и, следовательно, обладают лучшими точностными и динамическими свойствами, чем одноконтурные. Они проектируются для управления как одномерными, так и многомерными объектами управления.

Проанализируем использование линейных регуляторов состояния для решения задач стабилизации и слежения [15].

Рассмотрим задачу стабилизации объекта управления (ОУ) в точке Y^* = 0, полагая, что при этом вектор состояния также принимает нулевое значение: X^* = 0 (к такому виду задача почти всегда может быть приведена преобразованием координат векторов X и Y).

Простейший регулятор состояния - пропорциональный или модальный регулятор вводит обратные связи по всем переменным x_i (рис. 10.5).

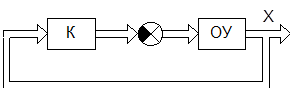
Рис. 10.5. Структурная схема системы с П-регулятором

Модальный регулятор реализует пропорциональный закон управления

U = - K´X, (10.38)

где K - матрица коэффициентов обратной связи по состоянию.

Для одномерного объекта управления в качестве координат x_i вектора X можно выбрать, например, фазовые переменные y, 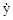,..., y^(n-1) , то есть

X = [ x₁ x₂ ... x_n ]^T = [ y 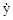... y^(n-1) ]^T , (10.39)

где 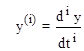; n - порядок системы.

Тогда K = [ k₁ k₂ ... k_n ]. Выражение (10.38) можно записать в скалярной форме

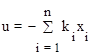. (10.40)

Первые члены закона управления (10.40) соответствуют описанию ПД-регулятора выхода при y^* = 0.

Таким образом, регуляторы состояния являются обобщением ПД-регуляторов, хотя и не содержат в явном виде дифференцирующих звеньев. Выбор коэффициентов k матрицы обратной связи K обеспечивает получение заданных динамических свойств системы.

В условиях действия на объект управления внешних возмущений F точностные показатели качества системы с пропорциональным регулятором состояния ограничены. Снижение установившихся ошибок достигается введением в состав регулятора контуров интегральных обратных связей (рис. 10.6).

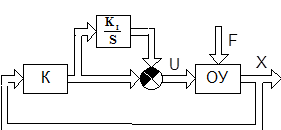
Рис. 10.6. Структурная схема системы с ПИ-регулятором

ПИ-регулятор реализует пропорционально-интегральный закон управления

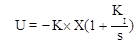, (10.41)

где K_I - матрица обратных связей по интегралу от вектора состояния.

Комбинированный регулятор позволяет обеспечить компенсацию возмущения за счет прямых связей по возмущающему воздействию F (рис. 10.7).

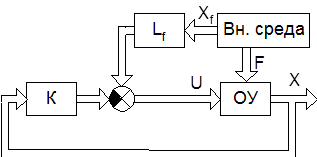
Рис. 10.7. Структурная схема комбинированной системы по возмущающему воздействию

В этом случае закон управления принимает вид

U = - K´X + L_F´X_F , (10.42)

где L_F - матрица коэффициентов контура связей по F;

X_F - вектор, составленный из возмущения F и его производных.

Задача слежения рассматривается как задача отработки расширенного вектора задания X^* = X^* (t). П-регулятор состояния в следящей системе вырабатывает управляющее воздействие, пропорциональное вектору отклонения e = X^* - X, то есть реализует закон управления

U = K´e. (10.43)

Для одномерного объекта управления с вектором состояния (10.39) выражение (10.43) можно переписать в скалярной форме

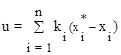, (10.44)

где x_i^* = (y^(i-1))^* .

ПИ-регулятор дополняет структуру системы интегральными связями:

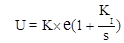. (10.45)

Эффективная компенсация ошибок, вызванных возмущающим воздействием F и изменениями задания X^* достигается использованием комбинированного управления (рис. 10.8)

U = K´e + L_X´X^* + L_F´X_F , (10.46)

где L_X - матрица коэффициентов контура прямых связей по X^*;

X^* - расширенный вектор задания;

L_F - матрица коэффициентов контура связей по F;

X_F - вектор, составленный из возмущения F и его производных.

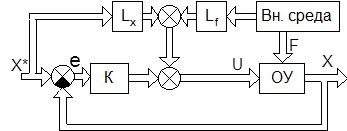
Рис. 10.8. Структурная схема комбинированной системы

Параметры регуляторов (коэффициенты прямых и обратных связей) определяются как функции параметров c математической модели объекта управления. Поэтому при управлении нестационарным объектом возникает необходимость изменения параметров регулятора в процессе работы системы. Задача настройки регулятора осложняется, когда параметры объекта управления неизвестны или неконтролируемо изменяются. Для управления такими объектами используются адаптивные регуляторы, параметры которых настраиваются с помощью блока адаптации (БА, рис. 10.9).

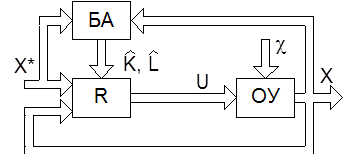
Рис. 10.9. Структурная схема адаптивной системы

Адаптивный регулятор состояния комбинированного типа содержит настраиваемые контуры обратных связей по состоянию X и прямых связей по расширенному вектору задания X^*. Закон управления такого регулятора

U = 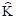´ e + 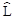´ X^*, (10.47)

где 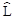, 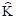- матрицы прямых и обратных связей с переменными коэффициентами (параметрами).

Функции блока адаптации заключаются в автоматической настройке параметров регулятора (10.47).

В практике адаптивных систем получили распространение два подхода к настройке параметров.

Первый из них предусматривает включение в состав системы блока идентификатора, осуществляющего вычисление неизвестных параметров объекта управления. Тогда после определения вектора c значения 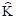и 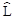могут быть найдены по известным, подготовленным заранее, зависимостям

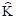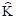= (c), 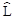= 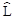(c). (10.48)

Второй подход (безидентификационный) позволяет осуществить настройку контура прямых связей части регулятора (10.47). При этом матрица обратных связей рассчитывается по номинальному значению вектора c и остается неизменной 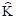= K_O. В качестве источника информации о параметрических ошибках регулятора в блоке адаптации используется сигнал обратной связи по отклонению:

U_e = K_O ´ e. (10.49)

Блок адаптации осуществляет изменение параметров регулятора до тех пор, пока в системе не установится нулевое значение сигнала обратной связи U_e и, следовательно, значение e будет равняться нулю.