Квадратичная регрессия

Аналогично находятся коэффициенты и для квадратичного приближения.

Имеем

y=a x²+bx+c.

Сумма квадратов невязок минимизируется путем выбора коэффициентов a,b,c, т.е.имеем

Ф(a,b,c)= e₁²+…+e_k² ®min

Где

ax_k²+bx_k+c-y_k=e_k

_n

Ф(a,b,c)= å (ax_k²+bx_k+c-y_k)²®min

^k=1

Далее

_n

∂Ф/∂а =0 å2(ax_k²+bx_k+c-y_k)x_k²=0 Þaåx_k⁴+båx_k³+cåx_k²=åy_kx_k²

ⁱ⁼¹

_n

∂Ф/∂b =0 å2(ax_k²+bx_k+c-y_k)x_k=0 Þaåx_k³+båx_k²+cåx_k=åy_kx_k

ⁱ⁼¹

_n

∂Ф/∂c =0 å2(ax_k²+bx_k+c-y_k) =0 Þaåx_k²+båx_k + nc=åy_k

ⁱ⁼¹

Теперь необходимо получить решение линейной системы алгебраических уравнений относительно коэффициентов квадратичной зависимости.

Рассмотренные выше подходы (интерполяции) реализуют концепцию «черного ящика», при которой ничего не известно о структуре исследуемой системы. В случае «серого ящика» известна структура объекта, например, дифференциальное уравнение, но не известны конкретные значения параметров 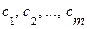. В этом случае задачу определения параметров можно свести к задаче параметрической оптимизации – минимизации ошибки моделирования. В качестве примера рассмотрим задачу определения параметров математического маятника, динамика которого описывается дифференциальным уравнением 2-го порядка

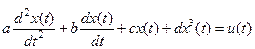(1)

Пусть из эксперимента известны функции воздействия на систему 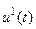и реакции на это воздействие 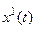на интервале времени 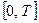. Ошибку моделирования можно определить как функцию параметров :

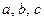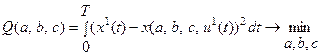, (2)

где 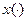– решение дифференциального уравнения (1).

Важно отметить, что такой подход можно использовать при рассмотрении нелинейных систем, систем с конечным временем и с ненулевыми начальными условиями. Обычно для реализации численных методов приходится вводить дискретное время 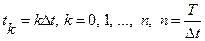. Тогда дифференциальный оператор можно заменить конечными разностями, интегральный − конечными суммами и минимизировать полученную сумму по параметрам. Ниже приведен документ MATHCAD (док. 1), решающий данную задачу. В нем показаны результаты идентификации нелинейного маятника, выходной сигнал которого замерен с нормальным шумом, сглажен процедурой скользящего среднего и использован для определения параметров.

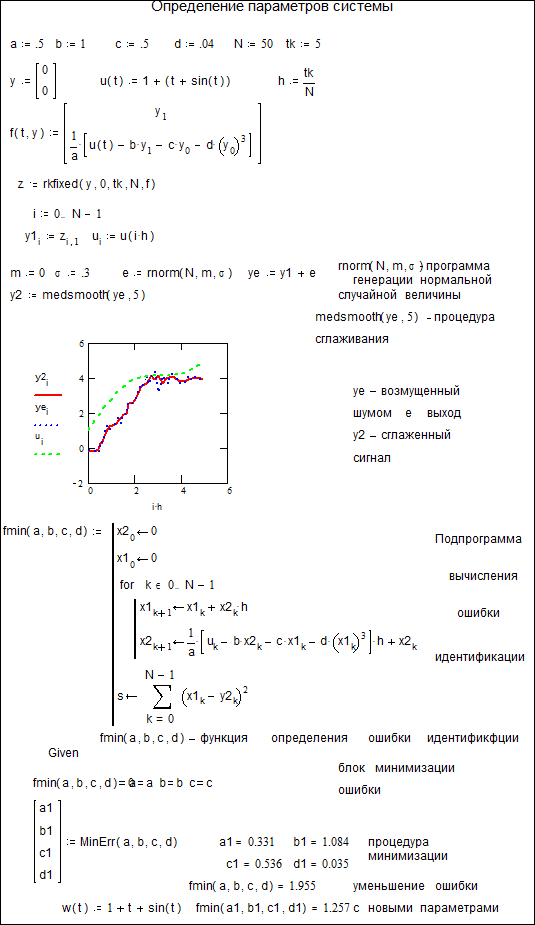
Док. 1

В следующем документе (док. 2) показаны результаты сравнения полученной модели с данными эксперимента.

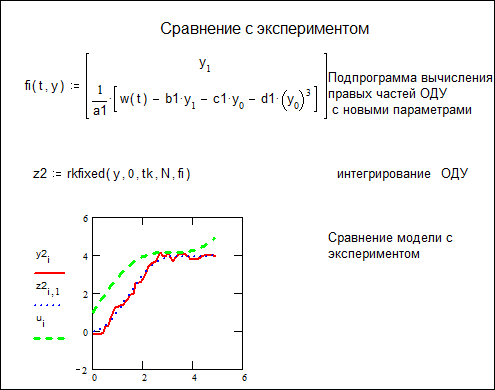
Док. 2

Центральный вопрос, рассматриваемый здесь – как по измерениям функций времени (входных и выходных сигналов) восстановить динамический оператор, описывающий динамическую модель исследуемого процесса.

Более благоприятна ситуация в случае известной структуры модели. Тогда имеют дело с «серым ящиком», и для построения модели нужно решить задачу определения неизвестных параметров. Известная е структура предполагает существенно меньшее количество неизвестных параметров. Общий подход к решению задач параметрической идентификации − это их сведение к задаче нелинейного программирования, то есть вычисление по решению дифференциального уравнения функции ошибки моделирования и ее минимизация по идентифицируемым параметрам.

Следует иметь в виду, что часто такие задачи являются плохо обусловленными. Иными словами, незначительные ошибки в исходных данных (например, ошибки измерений) могут привести к значительным ошибкам в определении модели. В этих условиях необходимо применять процедуры регуляризации решения, заключающиеся в наложении дополнительных условий на решение, например на ограничение его нормы.