Двойственная задача линейного программирования

Теорема Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем для экстремальных значений целевых функций обоих задач выполняется соотношение: max Исходной = min Двойственной и наоборот.

Следствие. Если целевая функция одной из задач не ограничена, то другая задача решения не имеет.

На практике, обычно решают ту задачу, которая несет основной содержательный смысл, а результаты решения другой используют по необходимости для экономического обоснования первой. При этом результаты решения как исходной так и двойственной задач находятся в одной и той же симплекс-таблице.

Существуют симметричные и несимметричные пары задач. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем в последней переменные могут быть и отрицательными.

В симметричных двойственных задачах системы ограничений обоих задач задаются неравенствами, причем на двойственные переменные налагается условие неотрицательности.

При построении двойственной задачи используют следующие правила:

Ø число переменных двойственной задачи должно быть равно числу основных ограничений исходной;

Ø коэффициентами целевой функции для двойственной задачи служат свободные члены системы ограничений исходной задачи;

Ø вид экстремума двойственной задачи противоположен экстремуму исходной;

Ø матрица основных ограничений двойственной задачи получается транспортированием аналогичной матрицы исходной задачи;

Ø свободными членами системы основных ограничений двойственной задачи служат коэффициенты целевой функции исходной задачи;

Ø система основных ограничений двойственной задачи описывается неравенствами, причем знаки неравенств противоположны указанным в исходной задаче.

По условиям дана следующая математическая модель исходной задачи:

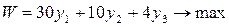
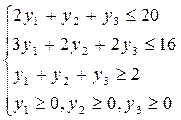(2.5.1)

Приведем ее к каноническому виду через ввод дополнительных переменных.

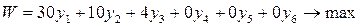
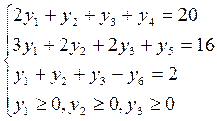(2.5.2)

Строим двойственную задачу по отношению к данной в соответствии с вышеизложенными правилами построения.

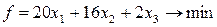
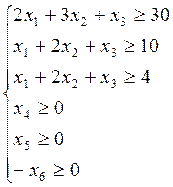(2.5.3.)

Решаем исходную задачу двойственным симплекс-методом. Для получения базиса следует умножить третье уравнение из системы ограничений на (-1).

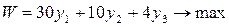
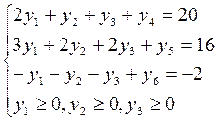(2.5.4.)

Переменные у₄, у₅, у₆ составляют базис. Можно составить исходную симплекс-таблицу.

Таблица 3

Базис	Сj							bi
У1	У2	У3	У4	У5	У6
У4
У5
У6		-1	-1	-1				-2
Wj- Сj	-30	-10	-4

В соответствии с алгоритмом метода покинуть базис должен вектор, имеющий отрицательную компоненту. Войдет в базис вектор У₁, т.к. его оценка минимальна. Соответственно генеральный элемент равен (-1).

Пересчитываем симплекс-таблицу и получаем следующий результат.

Таблица 4

Базис	Сj							bi
У1	У2	У3	У4	У5	У6
У4			-1	-1
У5			-1	-1
У1							-1
Wj- Сj						-30

План записанный в этой симплекс-таблице нельзя назвать оптимальным, т.к. есть вектор, чья оценка отрицательна. Поэтому вектор У₆ следует ввести в базис. Покинет базис вектор У₅,т.к. отношение компоненты к коэффициенту разложения вектора У₆ по базису у него минимально. Генеральный элемент равен 3. Пересчитываем план.

Таблица 5

Базис	Сj							bi
У1	У2	У3	У4	У5	У6
У4			-0,3333	-0,3333		0,6667		9,3333
У5			-0,3333	-0,3333		0,3333		3,3333
У1			0,6667	0,6667		0,3333		5,3333
Wj- Сj

Оценки всех векторов неотрицательны; значит, получен оптимальный план.

Результат: Wmax=160 у₁= 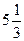у₂=0 у₃=0 у₄=9 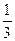у₅=0 у₆=3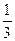

Двойственная задача имеет следующий результат:

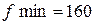х₁=0 х₂=0 х₃=0 х₄=0 х₅=10 х₆=16

Вопросы для самопроверки

1. Отличие линейного программирования от линейной алгебры.

2. Что такое область допустимых решений задачи линейного программирования.

3. Как находить оптимальное решение задачи с минимумом или максимумом целевой функции.

4. В чем достоинства и недостатки графического решения задачи линейного программирования.

5. Постановка задачи выбора оптимального промыслово-технологического режима работы добывающего судна.

6. Получение первой симплекс-матрицы задачи линейного программирования.

7. Правила преобразования симплекс-матриц при итеративном процессе.

8. Использование результатов преобразования симплекс-матриц.

9. Понятие о двойственной задаче линейного программирования.