Определение: Многочлен называется симметрическим если он не меняется при любой перестановке переменных.
Пример: 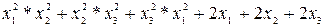 -симметрический многочлен
-симметрический многочлен
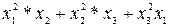 не симметрический.
не симметрический.
Строение симметрических многочленов можно представить в виде: Пусть 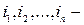 некоторая перестановка чисел 1,2,…,n. Если симметрический многочлен содержит член
некоторая перестановка чисел 1,2,…,n. Если симметрический многочлен содержит член 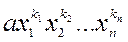 , то он и должен содержать член
, то он и должен содержать член 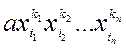 .
.
Симметрический многочлен является суммой однородных симметрических многочленов. Особую роль среди симметрических многочленов играют так называемые элементарные симметрические многочлены:
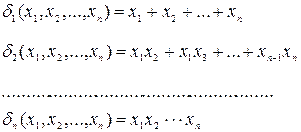
Определение: Многочлен называется однородным степени m, если все его члены имеют степень m.
Пример: 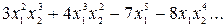
Очевидно, что сумма двух однородных многочленов одинаковой степени, есть однородный многочлен той же степени.
Произведение однородных многочленов степени 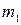 и
и 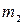 есть однородный многочлен степени
есть однородный многочлен степени 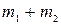 .
.
17. Многочлены над числовым полем.
Алгебраически замкнутое поле -это поле K в котором каждый многочлен не нулевой степени над полем K имеет хотя бы один корень.
Пример: поле комплексных чисел является алгебраически замкнутым.
Пример: поле действительных чисел не является алгебраически замкнутым, то есть: 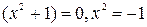
Свойства:
1) В алгебраически замкнутом поле K каждый многочлен степени n имеет ровно n корней в этом поле (с учетом кратности)
2) Конечные поля не могут быть алгебраически замкнутыми. Например: можно рассматривать многочлен конечной степени, корнями которого являются все элементы поля, если к нему прибавить единицу, то многочлен не будет иметь корней.
3) Алгебраическим замыканием поля действительных чисел является поле комплексных чисел, его алгебраическая замкнутость устанавливается основной теоремой алгебры.
4) Алгебраическим замыканием поля рациональных чисел является поле алгебраических чисел.
5) Поле арифметических чисел алгебраически замкнуто.
Определение: Число называется алгебраическим, если оно является корнем какого-либо алгебраического уравнения с целыми коэффициентами.
Пример: 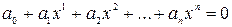
Теорема Виета: Если многочлен P(x) степени n имеет n различных корней 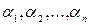 то имеет место следующие соотношения:
то имеет место следующие соотношения:
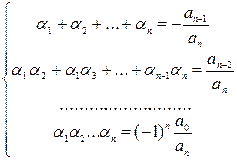
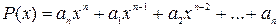
В случае, когда уравнение четвертой степени имеем: 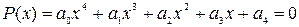 , где
, где 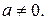
Корни будут: 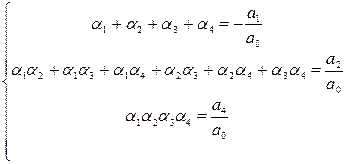
Основная теорема алгебры (теорема Гаусса): Всякий многочлен n-ой степени имеет по крайней мере один комплексный корень.
Следствие: Многочлен степени n с комплексными коэффициентами и со старшим коэффициентом 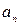 разлагается в произведение n сомножителей вида
разлагается в произведение n сомножителей вида 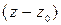 , то есть:
, то есть:
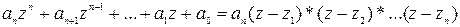
Теорема: Если многочлен с действительными коэффициентами имеет комплексный корень 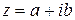 то он имеет и сопряженный корень
то он имеет и сопряженный корень 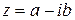 .
.
Теорема: Любой многочлен с действительными коэффициентами разлагается в произведение многочленов первой степени и второй степени (не имеющей действительных корней) с действительными коэффициентами.
Теорема: для того, чтобы несокращаемая дробь 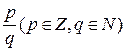 была корнем многочлена с целыми коэффициентами необходимо, чтобы число p было делителем свободного члена
была корнем многочлена с целыми коэффициентами необходимо, чтобы число p было делителем свободного члена 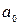 , а число q знаменателем старшего члена
, а число q знаменателем старшего члена 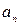 .
.
 2015-06-04
2015-06-04 3478
3478








