Простейшие следствия:
1. 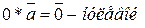 вектор
вектор
2. 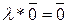 нулевой вектор
нулевой вектор
3. 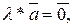 если
если 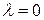 или
или 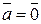 (
(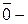 нулевой вектор)
нулевой вектор)
4. 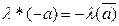
5. 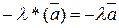
6. 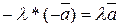
7. 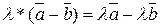
10. Линейная зависимость системы векторов. Базис и ранг конечной системы векторов.
Пусть дана система векторов 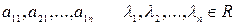
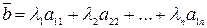 вектор
вектор 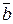 называется линейной комбинацией векторов
называется линейной комбинацией векторов 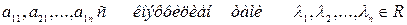
Определение: Векторы 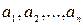 линейно зависимы или образуют линейно зависимую систему, если среди них находится вектор, который можно линейно выразить через остальные.
линейно зависимы или образуют линейно зависимую систему, если среди них находится вектор, который можно линейно выразить через остальные.
Определение: Если ни один из векторов нельзя представить в виде линейной комбинации векторов, то такая система векторов называется независимой.
Если система состоит из единственного вектора, то она является линейно зависимой только тогда, когда этот вектор является нулевым.
Система из двух векторов линейно зависима только тогда, когда векторы пропорциональны.
Определение: Система векторов 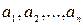 называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа 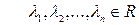 не равные одновременно нулю, такие что выполняется равенство:
не равные одновременно нулю, такие что выполняется равенство: 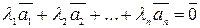 равно нулевому вектору.
равно нулевому вектору.
Определение: Система векторов 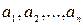 называется линейно независимой если выполняется равенство
называется линейно независимой если выполняется равенство 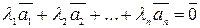 только в случае
только в случае 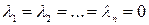
|
|
|
Пример: вектора 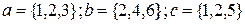
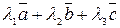 =0
=0
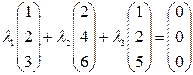
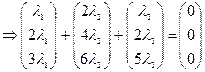
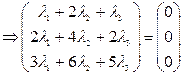
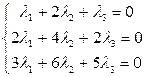 -решение методом Гаусса
-решение методом Гаусса
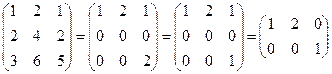
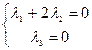
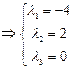
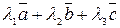 =0
=0
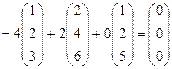 -система векторов линейно зависима.
-система векторов линейно зависима.
Пример: 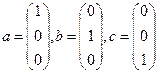
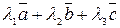 =0
=0 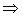
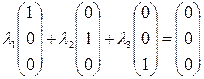
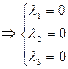 -система линейно независима.
-система линейно независима.
Пространственные свойства линейной зависимости:
- Если среди векторов системы имеется нулевой вектор, то система линейно зависима.
- Если часть системы линейно зависима, то и вся система линейно зависима.
- Если система линейно независима, но при добавлении к ней еще одного вектора становится линейно зависимой, то этот вектор линейно выражается через вектор исходной системы.
- Диагональная система векторов всегда линейно независима.
Теорема: В n-мерном пространстве любая система, состоящая более чем из n-векторов всегда линейно зависима.
Пусть даны две системы векторов: 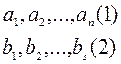 , где n>s
, где n>s
Тогда, если каждый вектор первой системы линейно выражается через вектор второй системы, то первая система линейно зависима.
Пусть в n-мерном векторном пространстве дана произвольная система векторов.
Определение: Подсистема 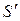 - есть базис системы S, если:
- есть базис системы S, если:
- она линейно независима
- добавление к подсистеме
 любого другого вектора из системы S превращает эту подсистему в линейно зависимую.
любого другого вектора из системы S превращает эту подсистему в линейно зависимую.
Другими словами, базис системы S линейно независимая подсистема, через которую линейно выражается любой вектор системы S.
Базис любой системы векторов n-мерного пространства всегда содержит не более чем n-векторов.
Теорема о базисах: Два различных вектора одной и той же системы векторов содержит одинаковое количество векторов.
Определение: Рангом системы векторов называется число векторов в любом базисе системы. Рангом системы векторов называется максимальное число линейно независимых векторов системы.
|
|
|
11. Системы линейных уравнений. Равносильные системы линейных уравнений.
Системой m линейных уравнений с n неизвестными называется система вида
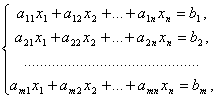
где aij и bi (i =1,…, m; b =1,…, n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс i- обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Если система уравнений имеет хотя бы одно решение, то она называется совместной.
Если система уравнений решений не имеет, то она называется несовместной.
Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной.
Если свободные члены всех уравнений системы равны нулю 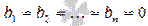 , то система называется однородной, в противном случае – неоднородной.
, то система называется однородной, в противном случае – неоднородной.
Две СЛАУ называют равносильными если каждое решение любой из этих систем является решением другой системы.
В матричной форме записи эта система уравнений имеет вид 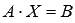 ,
,
где 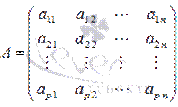 - основная матрица системы,
- основная матрица системы, 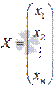 - матрица-столбец неизвестных переменных,
- матрица-столбец неизвестных переменных, 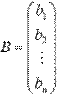 - матрица-столбец свободных членов.
- матрица-столбец свободных членов.
Определение: Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений.
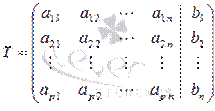
Элементарными преобразованиями называются такие преобразования расширенной матрицы, которые не меняют множество решений системы. Знак элементарного преобразования:  или ~.
или ~.
К элементарным преобразованиям относятся:
1)перемена строк метами.
2) перемена местами столбцов с запоминанием какому неизвестному соответствует каждый столбец.
3) умножение (деление) строки на число, отличное от нуля.
4) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.
5) вычеркивание одной из двух пропорциональных (в частности, равных) строк.
6) вычеркивание нулевой строки.
 2015-06-04
2015-06-04 1591
1591








