Применение ЛДУ к исследованию колебательных процессов. Резонанс

Рассмотрим электрическую цепь, состоящую из оптического сопротивления R, катушки L, ёмкости С, к которой подключён источник электродвижущей силы, изменяющейся с течением времени по закону: E = E (t).

Обозначим через i ток в цепи. Ток может изменяться с течением времени как по величине, так и по направлению, т.е. ток является функцией времени: i= i (t).

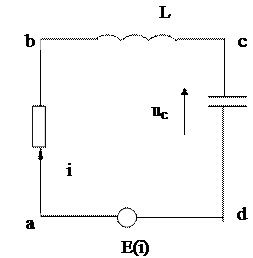Изменение тока во времени принято называть колебаниями тока. Определим через u_ab, u_bc, u_сd падения напряжения соответственно на участках ab, bc, cd цепи. Так как в замкнутом контуре алгебраическая сумма падений напряжения равна электродвижущей силе, то u_ab + u_bc, + u_сd = E (t).

Из физики известно, что

u_ab = RI (t) (закон Ома).

u_bc = L 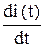; u_сd + .

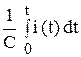Поэтому R_i (t) + L 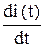+ 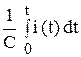= E (t). (1)

Дифференцируя по t обе части последнего равенства, получим

L 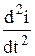+ R 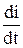+ 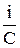= E' (2)

или 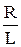i'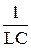' + i' + i = 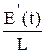. (2*)

Таким образом, искомая сила тока i в цепи является решением линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Оно называется уравнением вынужденных колебаний.

Если внешняя электродвижущая сила E постоянна (в частности, равна нулю), то E^I (t) = 0, и мы приходим к линейному дифференциальному уравнению без правой части

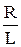i^II + i^I + 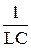i = 0. (3)

Оно называется уравнением свободных колебаний. Очевидно, что аналогичные уравнения можно составить и для напряжений.

Обозначим w₀ = 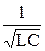и d = 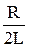; w₀ – называется собственной частотой свободных колебаний контура без потерь, d - коэффициент затухания. Запишем характеристическое уравнение ДУ (2); (3)

k² + 2dk + w 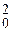= 0.

Решением дифференциальных уравнений (2), (2*), (3) будет зависеть от корней характеристического уравнения и от правой части.

Пусть переменная э.д.с. источника E = E₀ sin wt (w - называется частотой вынужденных колебаний). Тогда уравнение (2) примет вид:

L 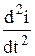+ R 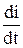+ 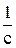i= E₀w cos wt. (4)

Решение этого уравнения будем искать в виде периодической функции о времени того же периода, что и период э.д.с.

i = i₀ sin (wt - j), (5)

где i₀, j - постоянные, которые нам надлежит определить. Составляя первую и вторую производные от i по времени, получим

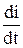= i₀w cos (wt - j); 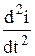= - i₀w² sin (wt - j).

Подставляя эти значения 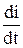; 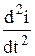, i Þ (4) и сокращая правую и левую части на w, найдём:

R i₀ cos (wt - j) – (Lw - 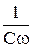) i₀ sin (wt - j) = E₀ cos wt.

Представляя cos (wt - j) и sin (wt - j) через синусы и косинусы от wt и j, получим:

i₀ (R cosj + (Lw – 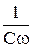cos wt + i₀ (R sinj - (Lw – 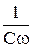) cosj) × sin wt =

= E₀ cos wt.

Так как это равенство должно выполняться для любого момента, то множители при sin wt и cos wt должны равняться

R sinj - (Lw – 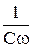) cosj = 0, (6)

R cosj + (Lw – 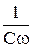) sinj = 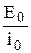. (7)

Из уравнения (6) получим: tg j = 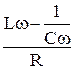. (8)

Возводя (6) и (7) почленно в квадрат и складывая их, найдём:

R² + (Lw – 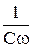)² = 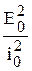, откуда:

i₀ = 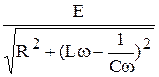(9)

Равенства (5), (8) (9) дают нам искомое решение: в цепи расчёт ток i того же периода, что и приложенная э.д.с. амплитуда этого тока i₀ определяется равенством (9).

Ток сдвинут по фазе относительно э.д.с. на угол j, определяемой равенством (8).

Величина z = 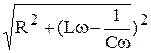- носит характер полного сопротивления (импеданс), она зависит от значений R, L, C и от частоты тока w. При w, удовлетворяющем соотношению Lw - 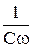= 0 (10), полное сопротивление достигает минимума; при этой частоте амплитуда силы тока достигает максимального значения:

i_0max = .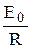

Из равенства (10) вытекает, что w = .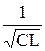

Получили, что амплитуда силы тока зависит от частоты w и достигает максимума при w₀ = 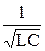, называемой резонансной частотой. Но выше была введена собственная частота свободного колебания w₀ = .

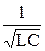Видим, что амплитуда силы тока достигает максимума при w = w₀, т.е. когда частота вынужденных колебаний равна собственной частоте свободного колебания.

Явление значительного возрастания амплитуды тока по мере приближения частоты вынужденных колебаний (частоты источника) к собственной частоте свободных колебаний (к частоте w₀) называется резонансом.

Итак, с помощью линейных дифференциальных уравнений можно исследовать колебания в электрических цепях.