Геометрические задачи

Приложения определенных интегралов

А. Вычисление площадей

а ) Вычисление площадей в прямоугольной системе координат.

Напомним геометрический смысл определенного интеграла - при определенных условиях он задает площадь криволинейной трапеции. Это позволяет находить площадь любой фигуры.

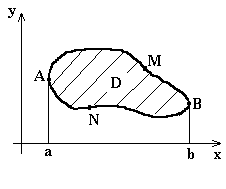
Точками А и В граница плоской фигуры D разбита на две части. Если известны уравнения “верхней” (дуга АМВ) и “нижней”(дуга ANB) границ:

АМВ: y = j₂ (x);

ANB: y = j₁ (x),

то площадь фигуры D можно найти как разность площадей, условно говоря, “большой “ и “малой” криволинейных трапеций:

S_D = S_aAMBb - S_aANBb =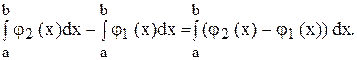

Очевидно, что формула останется справедливой для любого расположения области D (выше или ниже оси Ох). Например, если часть области D находится ниже оси Ох, то ее (область) можно перенести вверх на некоторое расстояние С таким образом, чтобы D оказалась целиком выше оси Ох. Величина площади от этого не изменится:

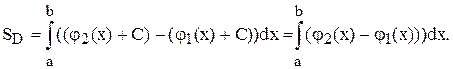
Пример. Найти площадь сегмента параболы, т.е. фигуры, ограниченной дугой параболы x = y² и отрезком прямой х = а.

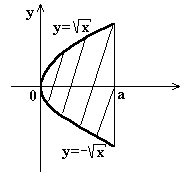
Решение. 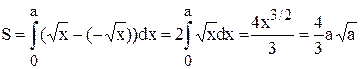(ед²).

б) Вычисление площадей в параметрической форме.

Если уравнение верхней границы криволинейной трапеции задано в параметрической форме: 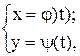причем a £ t £ b; j (a) = a; j (b) = b,

то, сделав замену переменной, получим:

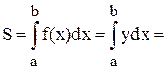{замена .

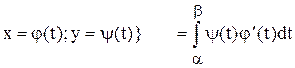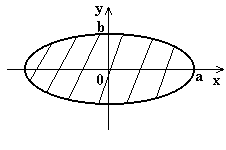
Пример. Найти площадь эллипса с полуосями а и b.

В прямоугольной системе координат уравнение эллипса имеет вид:

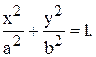
Используя симметрию фигуры, найдем площадь четверти эллипса:

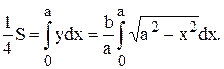
Используя параметрические уравнения эллипса в первой четверти:

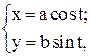
и учитывая, что при х = 0, t = 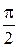; при х = а, t = 0, получим:

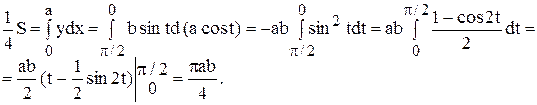
Тогда площадь эллипса будет: S = p ab.

в) Вычисление площадей в полярной системе координат.

Напомним, что площадь кругового сектора равна:

S _{кр.с. =}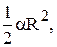

где a - центральный угол (в радианах),

R - радиус.

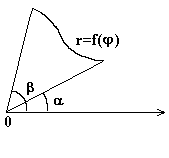
Рассмотрим криволинейный сектор, ограниченный лучами

j = a; j = b; и кривой r = f (j) (b > a).

Разобьем криволинейный сектор лучами, выходящими из полюса под углами j₁ = a; j₂,...., j_n = b, на n частей.

Обозначим Dj _i = j _i - j _i-1 и найдем площадь i - того (малого) криволинейного сектора, приближенно считая его круговым:

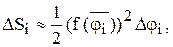
где 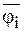- промежуточное значение угла между j _i-1 и j _i .

Тогда площадь всего кругового сектора будет равна:

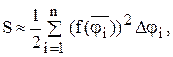
переходя к пределу при 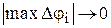, получим:

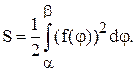
Пример. Найти площадь фигуры, ограниченной линией

(a² + y²)² = a²(x² - y²), называемой лемнискатой Бернулли (a > 0).

Т.к. переменные x, y входят в уравнение только в четных степенях, то фигура симметрична как относительно обеих осей координат, так и относительно начала координат. Перейдем к полярным координатам:

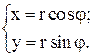
Подставив в уравнение линии, получим:

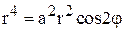или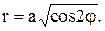

Построим линию, учитывая симметрию фигуры и условие r ³ 0.

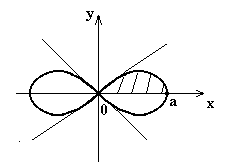
Площадь всей фигуры равна учетверенной площади заштрихованной части:

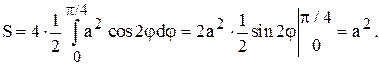
Б. ВЫЧИСЛЕНИЕ ДЛИН дуг кривЫХ

Если уравнение линии задано в прямоугольной системе координат:

y = f (x), причем f (x) и f¢ (x) непрерывны на отрезке [a; b], то длиной такой криволинейной дуги называется предел, к которому стремится длина вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю.

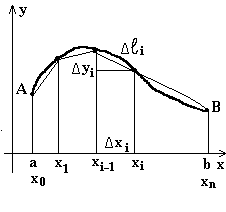
Если участок Dх_i достаточно мал, то:

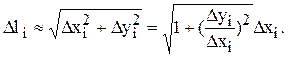
Сложив все “элементарные дуги” и перейдя к пределу, получим:

Dy_i = f(x_i) - f(x_i-1) = {по формуле Лагранжа} = f¢(C_i) Dx_i,

где С_i - промежуточное значение между x_i-1 и x_i.

Тогда: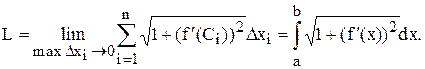

Если кривая задана в параметрической форме:

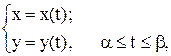
причем x(t), x¢(t), y(t), y¢(t) непрерывны на отрезке [a; b], то аналогичные рассуждения приведут нас к следующему результату:

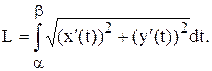
Если кривая задана в полярной системе координат:

r = r(j), a £ j £ b, то получим: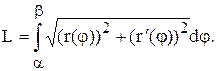

В. Вычисление объемов

Пусть дано тело, площадь каждого сечения которого плоскостью, перпендикулярной оси Ох, известно. Назовем эти сечения поперечными. Положение поперечного сечения зависит от абсциссы точки пересечения его с осью Ох.

Площадь сечения является некоторой функцией x: S = S(x), где x Î [a;b].

Для вычисления объема тела применим общий метод.

1. Разобьем отрезок [a; b] на n произвольных непересекающихся частей точками: х₀ = а, х₁, х₂,..., x_n-1, x_n = b.

Через точки деления проведем плоскости, перпендикулярные оси Ох. Тело разобьется на n слоев.

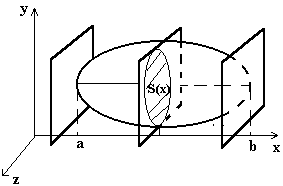
2. Обозначим объем слоя тела, соответствующий отрезку [x_i-1; x_i], через DV_i, -

тогда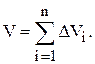

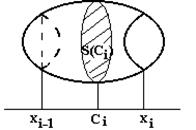
3. Вычислим объем i-го слоя. Для этого внутри [x_i-1; x_i] выберем точку С_i.

Вычислим S(C_i). Будем считать, что объем i- го слоя приближенно равен объему цилиндра, площадь основания которого равна S(C_i) и высота которого равна длине отрезка [x_i-1; x_i], т.е. Dx_i: DV_i» S(C_i)Dx_i.

4. Объем всего тела:

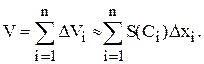
5. Переходя к пределу при l ® 0, где 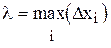получим: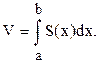

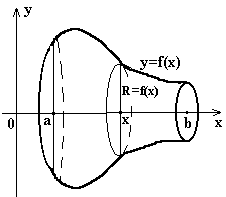
Объем тела вращения.

Пусть тело получается вращением трапеции, ограниченной линией

y = f(x), x Î [a;b], вокруг оси Ох, т.о. поперечным сечением служит круг, радиус которого равен соответствующей ординате кривой y = f(x).

(Если y < 0, то радиус будет равен ).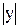

Площадь поперечного сечения S(x) = pR² = p[f(x)]², и мы приходим к формуле для объема тела вращения: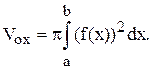

Замечание. Если требуется найти объем тела, образованного вращением трапеции, ограниченной линией x = f(y), y Î [c;d], вокруг оси Oy, то получим:

Итак, с помощью определённого интеграла можно вычислить площади, длины дуг кривых и объёма тел.

2. Решение простейших физических задач

Мы уже говорили, что, если f (x) есть величина переменной силы, то

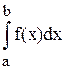выражает работу переменной силы по перемещению материальной точки вдоль прямолинейного пути.

Пример. По двум прямолинейным длинным параллельным проводникам, находящимся на расстоянии r₁ друг от друга, текут в одном направлении токи J₁ и J₂.

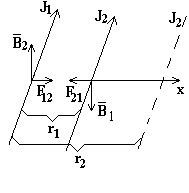
Какую работу (на единицу длины проводника) необходимо совершить, чтобы раздвинуть эти проводники до расстояния r₂?

Решение.

По закону Био-Савара-Лапласа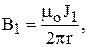

где r - расстояние между токами.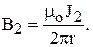

По закону Ампера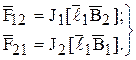

Тогда получим:

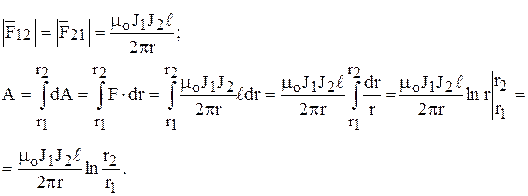
Рассмотрим еще некоторые случаи применения определенных интегралов.

В механике материальную плоскую фигуру принято называть пластинкой.

Пусть дана пластинка в форме криволинейной трапеции, ограниченной сверху кривой y = f(x), отрезком [a; b] оси Ох и прямыми x = a, x = b.

Пусть на этой пластинке масса распределена равномерно. Тогда, проводя аналогичные рассуждения, получим формулы для определения центра тяжести:

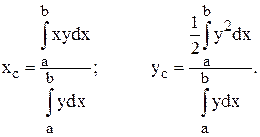
Статические моменты J_x и J_y плоской пластинки относительно осей координат вычисляются по формулам:

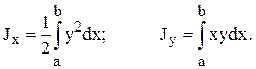
Таким образом, используя определённый интеграл можно решать физические задачи.