Шаг 1. Составить обобщенную функцию Лагранжа:
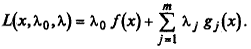
Шаг 2. Записать необходимые условия экстремума первого порядка:
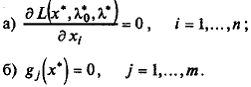
Шаг 3. Решить систему (3.12) для двух случаев:
1) λ0 * = 0;
2) λ0 * ≠ 0 (при этом поделить условие «а» на λ0 * и заменить 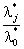 на λ j * ).
на λ j * ).
В результате найти условно-стационарные точки х *, выделив из них полученные при λ0 * ≠ 0 (они могут быть регулярными точками экстремума).
Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума:
а) записать выражение для второго дифференциала классической функции Лагранжа в точке (х *, λ *):
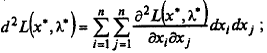
б) записать систему (3.12) в точке х *:
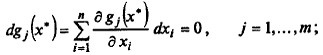
в) из предыдущей системы выразить любые т дифференциалов dxi через остальные (п – т) и подставить в d 2 L (х *, λ *);
г) если d 2 L (х *, λ *) > 0 при ненулевых dx, то в точке х * — условный локальный минимум. Если d 2 L (х *, λ *) < 0 при ненулевых d х, то в точке х * — условный локальный максимум. Если достаточные условия экстремума не выполняются, следует проверить выполнение необходимых условий второго порядка (см. утверждение 3.2), следуя аналогичной процедуре. Если они выполняются, то требуется дополнительное исследование, а если не выполняются, то в точке х* нет условного экстремума.
Шаг 5. Вычислить значения функции в точках условного экстремума.
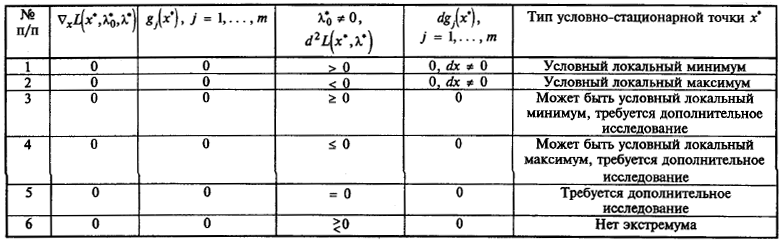
Условия экстремума в задаче (3.7) приведены в табл. 3.1.
Таблица 3.1
Необходимые и достаточные условия в задаче поиска
условного экстремума при ограничениях типа равенств
Пример 3.5. Найти экстремум функции 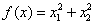 на множестве X = { х | х 1 + х 2 – 2 = 0}:
на множестве X = { х | х 1 + х 2 – 2 = 0}: 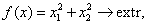 g 1 (x) = x 1 + х 2 – 2 = 0.
g 1 (x) = x 1 + х 2 – 2 = 0.
Проверим условие регулярности. Так как ∇ g 1 (x) = (l, l) T ≠ 0, то условие выполняется (см. определение 3.6). Поэтому будем пользоваться классической функцией Лагранжа (3.3).
1. Составим функцию Лагранжа:
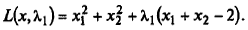
2. Выпишем необходимые условия экстремума первого порядка:
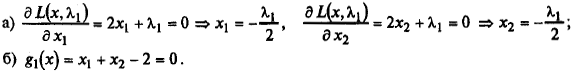
3. Решение системы: х 1 * = х 2 * = 1, λ1 * = –2 — условно-стационарная точка.
4. Проверим достаточные условия экстремума:
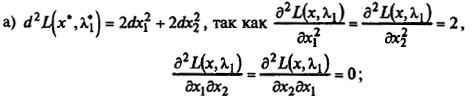
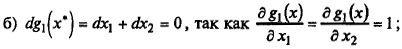
в) выразим дифференциал dx 1 через dx 2: dx 1 = – dx 2 подставим в d 2 L;
г) так как d 2 L (x *, λ1 *) = 4 dx 2 2 > 0 при dx 2 ≠ 0, то в точке x * = (l, l) T — регулярный локальный условный минимум (строка 1 в табл. 3.1). Графическое решение задачи приведено на рис. 1.7.
5. Подсчитаем значение функции в точке условного экстремума: f (x *) = 2.
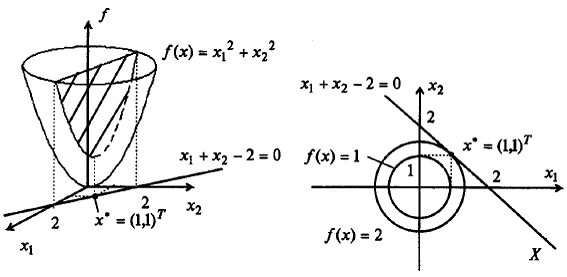
Рис. 1.7
 2015-06-04
2015-06-04 924
924








