Простейшие случаи понижения порядка
1. Уравнение вида y(n) =f(x) (случай непосредственного интегрирования).
В соответствии с определением производной n- ого порядка
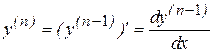
преобразуем исходное уравнение и проинтегрируем
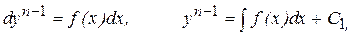
в результате чего порядок уравнения понизился.
Общее решение получается последовательным интегрированием
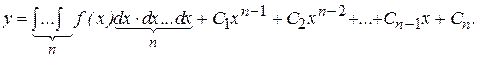
2. Уравнение вида F(x,y(k),y(k+1) ,...,y(n) )=0 (не содержит искомой функции и её производных до порядка к-1 включительно).
Порядок уравнения может быть понижен на к единиц заменой
y(k) =p(x).
Так как y(k+1) =p¢(x),..., y(n) =p(n-k) (x), уравнение примет вид
F(x,p,p¢,...,p(n-k) )=0.
Из последнего уравнения находим p=p(x,C1 ,C2 ,...,Cn-k), а у находим из уравнения y(k)=p(x,C1 ,C2 ,...,Cn-к) интегрированием к раз.
3. Уравнение вида F(y,y¢,y²,...,y(n))=0 (не содержит независимой переменной).
Понижение порядка уравнения на единицу достигается заменой y¢=р(у), причем следует обратить внимание на то, что р рассматривается как новая неизвестная функция аргумента у (а не х, как в предыдущем случае). Поэтому все производные функции у по аргументу х надо выразить через производные новой функции р(у) по аргументу у, учитывая что р является сложной функцией от х:
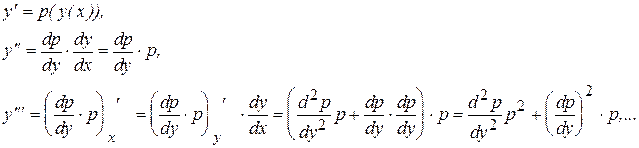
4. Порядок уравнения понижается на единицу в случаях, когда уравнение можно привести к виду
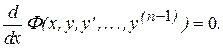
Откуда следует
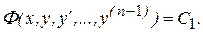
Замечание. Для рассмотренных выше уравнений вида 2-4 при решении задачи Коши в ряде случаев нецелесообразно находить общее решение уравнения. Решение упрощается, если начальные условия используются в процессе решения.
Пример 6. Решить уравнение 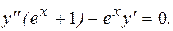
Решение. В этом уравнении отсутствует искомая функция y. Поэтому, вводим замену 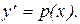 Тогда
Тогда 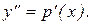
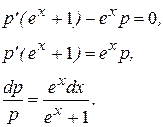
Интегрируя, получим
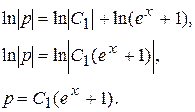
Возвращаясь к исходной функции y, имеем
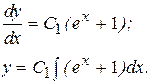
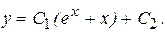
Пример 7. Найти частное решение уравнения 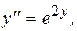 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 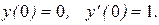
Решение. Это уравнение не содержит явным образом аргумента x. Поэтому используем замену 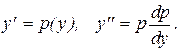
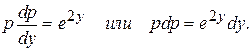
Интегрируя получим
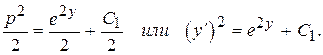
Тогда
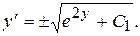
Так как 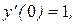 то
то 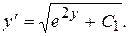
Используя начальные условия, найдем С1.
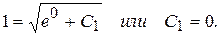
Получим уравнение
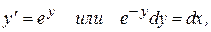
интегрируя которое, находим
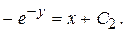
Из условия 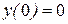 определим значение С2.
определим значение С2.
-1=0+С2, С2=-1.
Тогда
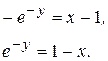
Прологарифмировав последнее равенство, выразим y.
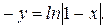
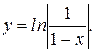
 2015-06-05
2015-06-05 973
973








