18. Условия, определяющая фигуру в аффинной и прямоугольной системах координат.
Фигурой называется любое множество точек.
Пусть даны любая система координат (на плоскости или в пространстве) и произвольная фигура Ф. Тогда каждая точка, в том числе и каждая точка фигуры, будут определяться своими координатами. Если точку в фигуре менять, то будут меняться и её координаты. Но (если только фигура не совпадает с плоскостью или пространством), меняясь, координаты точек фигуры будут удовлетворять каким-то условиям.
Определение 23. Условием, определяющим фигуру Ф в данной системе координат называется такое условие, которому удовлетворяют координаты любой точки, принадлежащей фигуре Ф, и не удовлетворяют координаты никаких других точек.
Примеры. Найти условия, определяющие следующие фигуры.
1. Ось (Ох) в аффинной системе координат на плоскости (рис. 26).М Î (Ох) Û 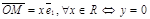 .
.
Следовательно, условие, определяющее ось (Ох) в аффинной системе координат на плоскости, есть у = 0 .
2. Ось (Ох) в аффинной системе координат в пространстве (рис. 27).М Î (Ох) Û 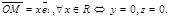
|
|
|
Следовательно, условие, определяющее ось (Ох) в аффинной системе координат в пространстве, есть 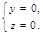
3. Окружность радиуса r с центром в точке М0(х0, у0) в прямоугольной системе координат на плоскости (рис. 28).
М Î окр(М0, r) Û ½М0М½ = r.
Перепишем последнее равенство в координатах, используя тот факт, что система координат прямоугольная.
М Î окр(М0, r) Û 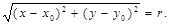
Так как в последнем равенстве обе части неотрицательны, то оно эквивалентно условию 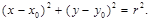 (12)
(12)
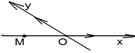
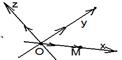
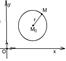
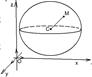
Рис. 26 Рис. 27 Рис.28 Рис.29
В приведённых примерах условия, определяющие фигуру, являются либо уравнениями, либо системами уравнений. Если условие, определяющее фигуру является уравнением или системой уравнений, то оно называется уравнением (уравнениями) данной фигуры. Так, уравнение оси (Ох) на плоскости у = 0. Уравнения оси (Ох) в пространстве 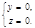 Уравнение окружности в прямоугольной системе координат на плоскости
Уравнение окружности в прямоугольной системе координат на плоскости 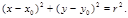
4. Шар радиуса r с центром С(х0, у0, z0) в прямоугольной системе координат в пространстве (рис. 29).
М Î шар (С, r) Û ½СМ½ £ r.
Перепишем последнее равенство в координатах, используя тот факт, что система координат прямоугольная.
М Î шар (С, r) Û 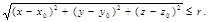
Так как в последнем равенстве обе части неотрицательны, то оно эквивалентно условию
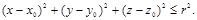 (13)
(13)
Обратная задача:
Пусть на плоскости (или в пространстве) зафиксирована аффинная система координат и задано условие, связывающее две (или три) переменные. Например, F(x, y) = 0. Если {(x, y)} - множество всех упорядоченных пар действительных чисел, удовлетворяющих данному условию, то в данной системе координат это множество определяет множество точек, т.е. фигуру.
|
|
|
Прямая в аффинной системе координат на плоскости и в пространстве
19. Уравнения прямой, проходящей через а) данную точку параллельно данному вектору; б) две данные точки. Уравнение прямой в отрезках.
а) данную точку параллельно данному вектору
На плоскости
Дано: R = 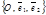 , М0(х0, у0), , М0(х0, у0), 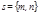 , , 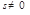 ,l ' M0,
l ½½ ,l ' M0,
l ½½  .
Найти условие, определяющее l.
Пусть М(х, у). .
Найти условие, определяющее l.
Пусть М(х, у).
 Рис. 30
М Î l Û
Рис. 30
М Î l Û  коллинеарен коллинеарен  Û
либо 1) Û
либо 1) 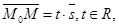 либо 2) координаты
либо 2) координаты 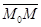 и и 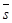 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 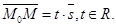 Если Если 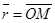 , , 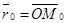 , то получим , то получим
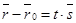 (14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим (14)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
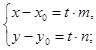 Отсюда Отсюда 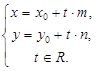 (15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты (15)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку параллельно данному вектору.
2) М Î l Û координаты 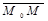 и и 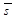 пропорциональны Û пропорциональны Û 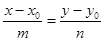 (16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. (16).
Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
| В пространстве
Дано: R = 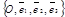 , М0(х0, у0, z0), , М0(х0, у0, z0),
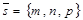 , , 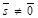 , l ' M0, l ½½ , l ' M0, l ½½ 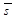 .
Найти условие, определяющее l.
Пусть М(х, у, z). .
Найти условие, определяющее l.
Пусть М(х, у, z).
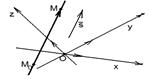 Рис. 301
М Î l Û
Рис. 301
М Î l Û 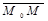 коллинеарен коллинеарен 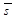 Û
либо 1) Û
либо 1) 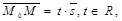 либо 2) координаты
либо 2) координаты 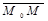 и и 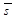 пропорциональны.
Рассмотрим оба случая.
1) М Î l Û пропорциональны.
Рассмотрим оба случая.
1) М Î l Û 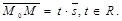 Если Если 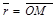 , , 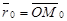 , то получим , то получим
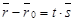 (141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим (141)
Это векторное уравнение прямой, проходящей через данную точку параллельно данному вектору.
Перепишем в координатах. Получим
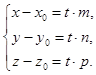 Отсюда Отсюда 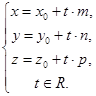 (151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку данному вектору.
2) М Î l Û координаты (151)
В полученных уравнениях t называется параметром, а уравнения – параметрическими уравнениями прямой, проходящей через данную точку данному вектору.
2) М Î l Û координаты 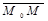 и и 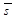 пропорциональны Û пропорциональны Û 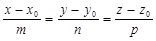 (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору. (161) Это канонические уравнения прямой, проходящей через данную точку параллельно данному вектору.
|
б) две данные точки.
На плоскости
Дано: R = 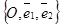 , М1(х1, у1), М2(х2, у2), М1 ¹ М2; l ' M1, l ' M2.
Найти уравнения l.
Так как М1 ¹ М2, то , М1(х1, у1), М2(х2, у2), М1 ¹ М2; l ' M1, l ' M2.
Найти уравнения l.
Так как М1 ¹ М2, то 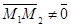 и l ½½ и l ½½ 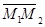 . Следовательно, можно использовать уравнения (15) и (16). Получим . Следовательно, можно использовать уравнения (15) и (16). Получим 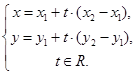 (17)
Это параметрические уравнения прямой, проходящей через две точки.
Из уравнения (16) получим (17)
Это параметрические уравнения прямой, проходящей через две точки.
Из уравнения (16) получим
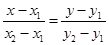 (18)
Это каноническое уравнение прямой, проходящей через две точки. (18)
Это каноническое уравнение прямой, проходящей через две точки.
| В пространстве
Дано: R = 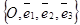 , М1(х1, у1,z1),
М2(х2, у2, z2), М1 ¹ М2; l ' M1, l ' M2.
Найти уравнения l.
Так как М1 ¹ М2, то , М1(х1, у1,z1),
М2(х2, у2, z2), М1 ¹ М2; l ' M1, l ' M2.
Найти уравнения l.
Так как М1 ¹ М2, то 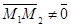 и l½½ и l½½ 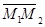 . Следовательно, можно использовать уравнения (151) и (161). Из уравнений (151) получим . Следовательно, можно использовать уравнения (151) и (161). Из уравнений (151) получим
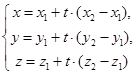 (171)
t ÎR.
Это параметрические уравнения прямой, проходящей через две точки.
Из уравнения (161) следует (171)
t ÎR.
Это параметрические уравнения прямой, проходящей через две точки.
Из уравнения (161) следует
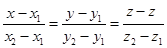 (181).
Это канонические уравнения прямой, проходящей через две точки. (181).
Это канонические уравнения прямой, проходящей через две точки.
|
Уравнение прямой в отрезках.
Уравнение прямой линии, пересекающей ось 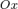 в точке
в точке 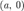 и ось
и ось 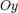 в точке
в точке 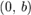 :
:
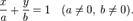
В этом виде невозможно представить прямую, проходящую через начало координат.
20. Общее уравнение прямой.
Из уравнений (16) и (18) видно, что любую прямую на плоскости можно задать уравнением первой степени с двумя переменными. Возникает обратный вопрос: всякое ли уравнение первой степени с двумя переменными задаёт в аффинной системе координат на плоскости некоторую прямую? Аналогично, уравнения (161) и (181) эквивалентны системе двух независимых уравнений первой степени с тремя переменными. Поэтому возникает обратная задача: Любая ли система двух независимых уравнений первой степени с тремя переменными задаёт в аффинной системе координат в пространстве прямую?
I.Общее уравнение прямой на плоскости
Дано: R = 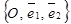 и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
Показать, что данное уравнение определяет прямую.
Доказательство. Пусть В ¹ 0. При х0 = 0 из данного уравнения получаем у0 = 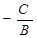 . Вектор
. Вектор 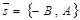 не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½
не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½ 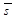 . Запишем уравнение l, используя (16). Получим
. Запишем уравнение l, используя (16). Получим 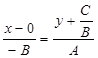 . После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
. После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
|
|
|
Уравнение Ах + Ву + С = 0 называется общее уравнение прямой на плоскости. При этом из доказательства следует, что вектор 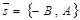 параллелен этой прямой.
параллелен этой прямой.
II. Общие уравнения прямой в пространстве
Дано: R = 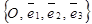 и система
и система 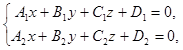 (19), где коэффициенты А1, В1, С1 не пропорциональны коэффициентам А2, В2, С2.
(19), где коэффициенты А1, В1, С1 не пропорциональны коэффициентам А2, В2, С2.
Показать, что данная система определяет прямую.
Доказательство. Пусть (х0, у0, z0) – одно из решений данной системы, т.е. 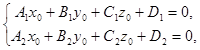 Вычтем из данной системы почленно полученные тождества. Получим систему
Вычтем из данной системы почленно полученные тождества. Получим систему 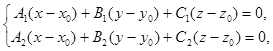 (*), эквивалентную данной. Это система двух линейных однородных уравнений с тремя переменными. Так как её коэффициенты не пропорциональны, то эта система имеет бесконечно много решений, причём все решения пропорциональны. Следовательно, достаточно найти одно ненулевое решение. Таким решением будет тройка
(*), эквивалентную данной. Это система двух линейных однородных уравнений с тремя переменными. Так как её коэффициенты не пропорциональны, то эта система имеет бесконечно много решений, причём все решения пропорциональны. Следовательно, достаточно найти одно ненулевое решение. Таким решением будет тройка 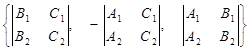 . Проверим это подстановкой. Подставим в первое уравнение:
. Проверим это подстановкой. Подставим в первое уравнение: 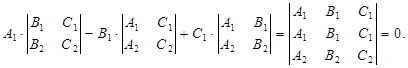 Подставим во второе уравнение:
Подставим во второе уравнение: 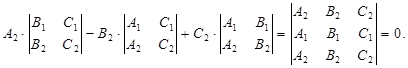 Итак, тройка
Итак, тройка 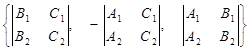 удовлетворяет обоим уравнениям системы (*). Эта тройка не нулевая. Следовательно, все решения системы (*) можно записать в виде
удовлетворяет обоим уравнениям системы (*). Эта тройка не нулевая. Следовательно, все решения системы (*) можно записать в виде
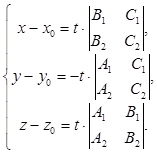 или
или 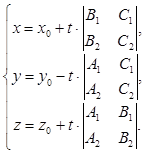 (20)
(20)
Итак, система 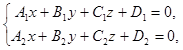 эквивалентна системе (20). Но система (20) это параметрические уравнения прямой. Следовательно, уравнения (19) задают прямую в аффинной системе координат в пространстве.
эквивалентна системе (20). Но система (20) это параметрические уравнения прямой. Следовательно, уравнения (19) задают прямую в аффинной системе координат в пространстве.
Уравнения (19) называются общие уравнения прямой в пространстве. Если прямая задана уравнениями (19), то вектор 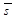 =
= 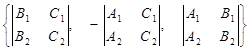 параллелен данной прямой.
параллелен данной прямой.
Замечание. Если прямая в пространстве задана общими уравнениями, то для приведения их к параметрическому (или каноническому виду) достаточно найти одно решение (х0, у0, z0) этих уравнений, найти вектор 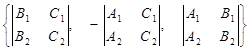 и использовать уравнение (20) или
и использовать уравнение (20) или 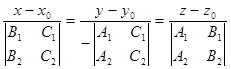 .
.
21. Исследование взаимного расположения двух и трёх прямых.
I. Исследовать взаимное расположение прямых, заданных общими уравнениями в АСК на плоскости.
Дано. R =  , l1: A1 x + B1 y + C1 = 0, l2: A2 x + B2 y + C2 = 0.
, l1: A1 x + B1 y + C1 = 0, l2: A2 x + B2 y + C2 = 0.
Исследовать взаимное расположение l1 и l2.
Исследование. Взаимное расположение прямых на плоскости зависит от числа их общих точек. Точка является общей для двух прямых тогда и только тогда, когда её координаты удовлетворяют уравнениям обеих прямых, т.е. удовлетворяют системе уравнений
|
|
|
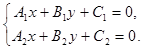 (21)
(21)
Таким образом геометрическая задача сведена к алгебраической – к исследованию системы двух уравнений с двумя неизвестными. Из курса алгебры известно, что для такой системы возможны три случая.
1. 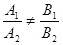 . В этом случае система (21) имеет единственное решение. На геометрическом языке это означает, что прямые l1 и l2 имеют одну общую точку, т.е. пересекаются. Итак, условие
. В этом случае система (21) имеет единственное решение. На геометрическом языке это означает, что прямые l1 и l2 имеют одну общую точку, т.е. пересекаются. Итак, условие 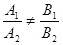 есть условие пересечения прямых, заданных общими уравнениями.
есть условие пересечения прямых, заданных общими уравнениями.
2. 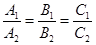 . В этом случае уравнения системы (21) эквивалентны, т.е. все решения одного из них являются решениями другого. На геометрическом языке – все точки одной прямой лежат на другой, т.е. прямые совпадают.
. В этом случае уравнения системы (21) эквивалентны, т.е. все решения одного из них являются решениями другого. На геометрическом языке – все точки одной прямой лежат на другой, т.е. прямые совпадают.
3. 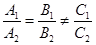 . В этом случае система (21) не имеет ни одного решения. На геометрическом языке – прямые l1 и l2 не имеют ни одной общей точки.
. В этом случае система (21) не имеет ни одного решения. На геометрическом языке – прямые l1 и l2 не имеют ни одной общей точки.
Если вспомнить определение: прямые l1 и l2 называются параллельными, если они лежат в одной плоскости и либо совпадают, либо не имеют ни одной общей точки, то получаем, что прямые l1 и l2 параллельны тогда и только тогда, когда 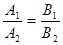 .
.
II. Исследовать взаимное расположение прямых на плоскости в АСК, если одна из прямых задана общим уравнением, а вторая – параметрическими уравнениями.
Дано. R = 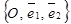 , l1: A x + B y + C = 0, l2:
, l1: A x + B y + C = 0, l2: 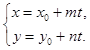
Исследовать взаимное расположение l1 и l2.
Исследование. Взаимное расположение прямых на плоскости зависит от числа их общих точек. Точка является общей для двух прямых тогда и только тогда, когда её координаты удовлетворяют уравнениям обеих прямых, т.е. удовлетворяют системе уравнений
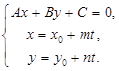 (22)
(22)
Подставив выражения х и у в первое уравнение и приведя подобные, получим
t* (Am + Bn) + (Ax0 + By0 + C) = 0 (23)
Для уравнения (23) возможны три случая.
1. Am + Bn ¹ 0. В этом случае Уравнение (23) имеет одно решение. На геометрическом языке это значит, что l1 и l2 имеют одну общую точку. Получили условие пересечения прямых.
2. Am + Bn = 0 и Ax0 + By0 + C = 0. В этом случае уравнение (23) имеет вид 0* t + 0 = 0. Этому уравнению удовлетворяют все t Î R. На геометрическом языке это значит, что все точки второй прямой принадлежат первой прямой, т.е. прямые совпадают.
3. Am + Bn = 0, но Ax0 + By0 + C ¹ 0. Уравнение (23) не имеет решения. Следовательно, прямые l1 и l2 не имеют ни одной общей точки.
Из случаев 2 и 3 получаем: прямые l1 и l2 параллельны тогда и только тогда, когда Am + Bn = 0.
III. Исследовать взаимное расположение двух прямых в АСК в пространстве, если прямые заданы параметрическими (или каноническими) уравнениями.
Дано: R = 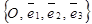 ,
, 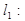
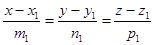 ,
, 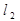 :
: 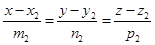 .
.
Исследовать взаимное расположение l1 и l2.
Исследование. Из уравнений первой прямой М1(х1, у1, z1) Î l1, 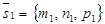 ,
, 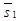 ½½l1. Из уравнений второй прямой М2(х2, у2, z2) Î l2,
½½l1. Из уравнений второй прямой М2(х2, у2, z2) Î l2, 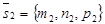 ,
, 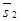 ½½l2. Возможны следующие случаи.
½½l2. Возможны следующие случаи.
1. l1½½l2 Û 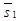 ½½
½½ 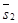 Û
Û 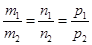 .
.
2. l1= l2 Û 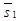 ½½
½½ 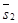 и М1 Î l2 Û
и М1 Î l2 Û 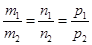 и
и 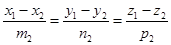 .
.
3. l1 пересекает l2 Û векторы 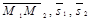 компланарны Û
компланарны Û 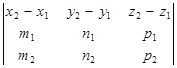 = 0.
= 0.
4. l1 скрещивается с l2 Û векторы 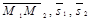 не компланарны Û
не компланарны Û 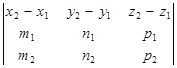 ¹ 0.
¹ 0. 
22. Уравнения прямой, проходящей через данную точку
а) перпендикулярно данному вектору;
Дано: R = 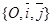 , М0(х0, у0),
, М0(х0, у0),  ,
, 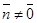 , l ' M0, l ^
, l ' M0, l ^ 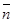 .
.
Найти уравнение l.
Найти уравнение l – это значит найти условие, которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек.
М Î l Û либо 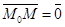 , либо
, либо 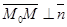 Û
Û 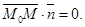 (*)
(*)
Так как 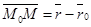 , то (*) перепишется
, то (*) перепишется 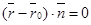 (24)
(24)
Полученное уравнение – это векторное уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Переписав уравнение (24) в координатах, получим
А(х - х0) + В(у - у0) = 0 (25)
Поставим обратную задачу:
Дано: R =  , l: Ax + By + C = 0 (*).
, l: Ax + By + C = 0 (*).
Доказать: если 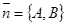 , то
, то 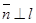 .
.
Доказательство. Пусть М(х, у) – произвольная точка данной прямой и М0(х0, у0) – некоторая фиксированная её точка. Тогда Ах0 + Ву0 + С = 0. Вычитая почленно полученное тождество из уравнения (*), получим уравнение А(х - х0) + В(у - у0) = 0, эквивалентное уравнению (*), т.е. уравнение (25). Если 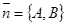 , то (25) можно записать
, то (25) можно записать 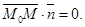 Вектор
Вектор 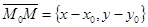 либо нулевой, либо параллелен l. Так как
либо нулевой, либо параллелен l. Так как 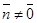 , то для всех точек М Î l, отличных от М0, имеет место
, то для всех точек М Î l, отличных от М0, имеет место 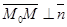 . Отсюда следует, что
. Отсюда следует, что 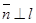 .
.
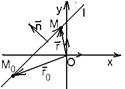
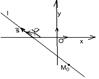
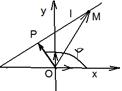
Рис.35 Рис.36 Рис. 37
б) под данным углом к оси (ОХ). Уравнение прямой с угловым коэффициентом.
Дано: R = 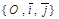 , М0(х0, у0), l ' М0,
, М0(х0, у0), l ' М0, 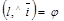 (угол j ориентированный).
(угол j ориентированный).
Найти уравнение l.
Для решения задачи достаточно знать вектор, параллельный данной прямой. Возьмём вектор 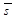 такой, что
такой, что 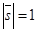 и
и 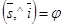 . Очевидно,
. Очевидно, 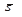 ½½ l. Так как координаты вектора в прямоугольной системе координат равны ортогональным проекциям этого вектора на соответствующие оси, то
½½ l. Так как координаты вектора в прямоугольной системе координат равны ортогональным проекциям этого вектора на соответствующие оси, то 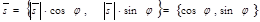 . Используя каноническое уравнение прямой на плоскости (16), получим
. Используя каноническое уравнение прямой на плоскости (16), получим
l: 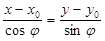 (26)
(26)
Прямые, не перпендикулярные оси (О х) называются наклонными. Для таких прямых 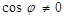 , следовательно, уравнение (26) можно привести к виду
, следовательно, уравнение (26) можно привести к виду
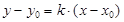 , где
, где 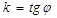 (27)
(27)
Если l ^ (О х), то уравнение (26) можно привести к виду х = х0 (28) Это уравнение вертикальной прямой.
Если l – наклонная прямая и l Ç (О у) = В, где В(0, в), то уравнение (27) преобразуется к виду у = к×х + в (29)
Уравнение (29) называют уравнение прямой с угловым коэффициентом. В этом уравнении к – тангенс угла наклона прямой к оси (О х), в – отрезок, отсекаемый прямой на оси (О у).
23. Нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду.
Дано: R =  ,
,  :
: 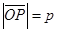 ,
, 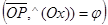 , l ' Р, l ^
, l ' Р, l ^ 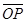 .
.
Найти уравнение l.
М Î l Û пр 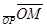 = р. Отсюда М Î l Û
= р. Отсюда М Î l Û 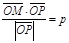 . Так как
. Так как 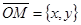 ,
, 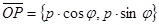 , то М Î l Û
, то М Î l Û 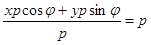 . Отсюда М Î l Û
. Отсюда М Î l Û 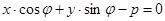 (30)
(30)
Уравнение (30) называется нормальное уравнение прямой. В этом уравнении
(cosj)2 + (sinj)2 = 1, свободный член (-р) £ 0.
Очевидно, нормальное уравнение прямой является одним из общих её уравнений. Если прямая задана в аффинной системе координат уравнением Ax + By + C = 0, то все остальные её общие уравнения имеют вид lAx + lBy + lC = 0, где l ¹ 0 (*). Следовательно, существует такое l, при котором уравнение (*) будет нормальным уравнением данной прямой. Для этого должны выполняться условия (lА)2 + (lВ)2 = 1, (lС) £ 0. Отсюда 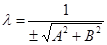 и знак перед корнем должен быть противоположен знаку С. (Если С = 0, то знак можно взять любой). Коэффициент
и знак перед корнем должен быть противоположен знаку С. (Если С = 0, то знак можно взять любой). Коэффициент 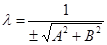 называется нормирующим множителем, а уравнение
называется нормирующим множителем, а уравнение 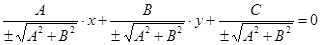 будет нормальным уравнением данной прямой. Говорят, что уравнение Ax + By + C = 0 приведено к нормальному виду.
будет нормальным уравнением данной прямой. Говорят, что уравнение Ax + By + C = 0 приведено к нормальному виду.
24. Угол между прямыми, заданными а) общими уравнениями;
Дано: R = 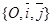 , l1: A1x + B1y + C1 = 0, l2: A2x + B2y + C2 = 0.
, l1: A1x + B1y + C1 = 0, l2: A2x + B2y + C2 = 0.
Найти один из углов 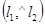 .
.
Замечание. Очевидно, достаточно найти только один из углов между прямыми.
Решение: Первый способ. Из уравнений l1 и l2 следует, что вектор 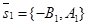 параллелен прямой l1 и вектор
параллелен прямой l1 и вектор 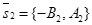 параллелен прямой l2. Следовательно, один из углов между l1 и l2 равен углу
параллелен прямой l2. Следовательно, один из углов между l1 и l2 равен углу 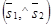 . Итак,
. Итак,
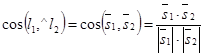 . (31)
. (31)
(Вывод формулы (31) можно проводить в любой аффинной системе координат). Воспользовавшись тем, что данная система координат прямоугольная, перепишем формулу (31) в координатах. Получим 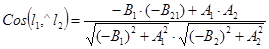 . Окончательно получим
. Окончательно получим
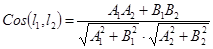 (32)
(32) 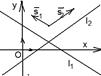
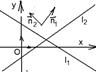
Рис 38 Рис. 39
Второй способ. Из уравнений l1 и l2 следует, что вектор 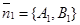 перпендикулярен прямой l1 и вектор
перпендикулярен прямой l1 и вектор 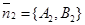 перпендикулярен прямой l2. Из свойства углов со взаимно перпендикулярными сторонами следует, что один из углов между l1 и l2 равен углу
перпендикулярен прямой l2. Из свойства углов со взаимно перпендикулярными сторонами следует, что один из углов между l1 и l2 равен углу 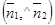 . Итак,
. Итак,
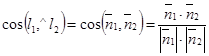 (33)
(33)
Переписав полученную формулу в координатах, получим
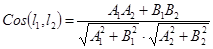 . (32)
. (32)
Замечание. Формулу (32) можно использовать только в том случае, когда прямые заданы общими уравнениями в прямоугольной системе координат.
Следствие. Две прямые перпендикулярны тогда и только тогда, когда А1А2 + В1В2 = 0 (33).
Задача 12. Дано. R = 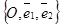 ,
, 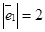 ,
, 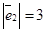 ,
, 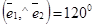 , l1: 3х - 4у + 11 = 0,
, l1: 3х - 4у + 11 = 0,
l2: 5х + у + 8 = 0.
Найти 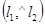 .
.
Решение. Используем формулу (31). В нашем случае 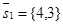 =
= 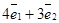 ,
, 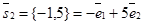 . Следовательно,
. Следовательно, 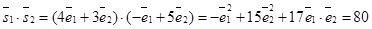 ;
; 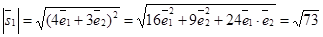 ,
, 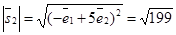 . Подставив в формулу (31), получим
. Подставив в формулу (31), получим 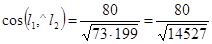 .
.
б) уравнениями с угловыми коэффициентами.
Дано: R =  , l1: у = к1× х + в1, l2: у = к2× х + в2.
, l1: у = к1× х + в1, l2: у = к2× х + в2.
Найти ориентированный угол, на который нужно повернуть l1, чтобы она стала параллельной l2.
Решение. Из уравнений l1 и l2 следует, что 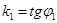 ,
, 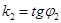 , где j1 и j2 – углы наклона прямых l1 и l2 к оси (Ох). Обозначим q ориентированный угол между l1 и l2 . По свойству внешнего угла треугольника получим q = j2 - j1. Отсюда
, где j1 и j2 – углы наклона прямых l1 и l2 к оси (Ох). Обозначим q ориентированный угол между l1 и l2 . По свойству внешнего угла треугольника получим q = j2 - j1. Отсюда
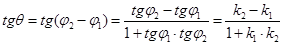 . Итак,
. Итак, 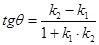 (34)
(34) 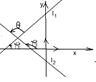
Рис. 40
Следствие. Две наклонные прямые перпендикулярны тогда и только тогда, когда
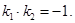 (35)
(35)
Задача. Дано: R =  , l1: 3х + 4у +12 = 0, l2: 4х - 7у - 1 = 0.
, l1: 3х + 4у +12 = 0, l2: 4х - 7у - 1 = 0.
Найти тангенс угла между прямыми l1 и l2. Решение. Используем формулу (34). Для этого нужно найти угловые коэффициенты данных прямых. Разрешая уравнения прямых относительно у, получим, что 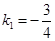 ,
, 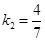 . Следовательно,
. Следовательно, 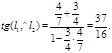
Задача 13. Дано: R = 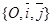 , l1: 3х + 4у +12 = 0, l2: 4х + 3у - 24 = 0. Найти уравнения биссектрис углов, образованных l1 и l2. Решение. Если l3 и l4 – биссектрисы данных углов, то каждая из них проходит через точку А = l1 Ç l2. Координаты точки А найдём, решая систему уравнений
, l1: 3х + 4у +12 = 0, l2: 4х + 3у - 24 = 0. Найти уравнения биссектрис углов, образованных l1 и l2. Решение. Если l3 и l4 – биссектрисы данных углов, то каждая из них проходит через точку А = l1 Ç l2. Координаты точки А найдём, решая систему уравнений 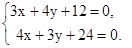 Получим А(
Получим А(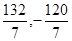 ). По определению биссектрисы
). По определению биссектрисы 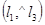 =
= 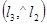 и
и 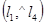 =
= 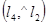 . Обозначим через к угловые коэффициенты l3 и l4. Используя формулу (34), получим
. Обозначим через к угловые коэффициенты l3 и l4. Используя формулу (34), получим 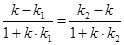 .Так как
.Так как 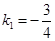 и
и 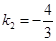 , то
, то 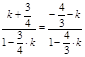 , или
, или 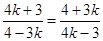 . Отсюда
. Отсюда 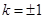 . Следовательно,
. Следовательно, 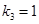 ,
, 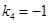 . Используя уравнение (27), получим l3: (у +
. Используя уравнение (27), получим l3: (у + 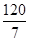 ) = 1×(х -
) = 1×(х - 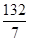 ). После упрощения l3: х - у - 36 =0.
). После упрощения l3: х - у - 36 =0.
Аналогично, l4: (у + 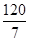 ) = -1×(х -
) = -1×(х - 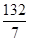 ). После упрощения l4: 7х + 7у - 12 =0.
). После упрощения l4: 7х + 7у - 12 =0.
25. Расстояние от точки до прямой.
Дано: R = 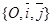 , l: Ax + By + C = 0, М0(х0, у0).
, l: Ax + By + C = 0, М0(х0, у0).
Найти d (M0, l).
Решение. Опустим из точки М0 на данную прямую перпендикуляр. Пусть N – его основание и N(х1,у1). Тогда Ax1 + By1 + C = 0 (*). Искомое расстояние d (M0, l) = 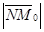 .
.  Если
Если 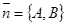 , то
, то 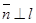 . Следовательно, векторы
. Следовательно, векторы 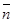 и
и 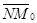 коллинеарны. Так как
коллинеарны. Так как 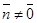 , то
, то 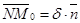 (**). Отсюда следует
(**). Отсюда следует
d (M0, l) = 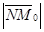 =
= 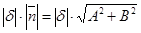 . (***)
. (***)  Рис. 41
Рис. 41
Для решения задачи достаточно найти 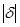 . Для этого обе части равенства (**) умножим скалярно на вектор
. Для этого обе части равенства (**) умножим скалярно на вектор 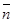 , получим
, получим 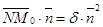 . Полученное равенство перепишем в координатах: А(х0 - х1) + В(у0 - у1) = d× (А2 + В2). Отсюда Ах0 + Ву0 - (Ах1 + Ву1) = d× (А2 + В2). Из (*) Ах1 + Ву1 = С. Следовательно, Ах0 + Ву0 + С = d× (А2 + В2) и
. Полученное равенство перепишем в координатах: А(х0 - х1) + В(у0 - у1) = d× (А2 + В2). Отсюда Ах0 + Ву0 - (Ах1 + Ву1) = d× (А2 + В2). Из (*) Ах1 + Ву1 = С. Следовательно, Ах0 + Ву0 + С = d× (А2 + В2) и 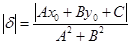 . Подставив в (***), получим d (M0, l) =
. Подставив в (***), получим d (M0, l) = 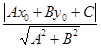 (35)
(35)
26. Геометрический смысл неравенств Ах + Ву + С £ 0 (< 0, > 0, ³ 0).
Дано. R = 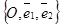 , Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
, Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
Исследовать, какую фигуру задаёт неравенство (38).
Решение. Пусть l: Ах + Ву + С = 0. Если бы вектор  был параллелен прямой l, то векторы
был параллелен прямой l, то векторы 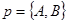 и
и 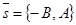 были бы коллинеарны. Но тогда
были бы коллинеарны. Но тогда 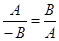 . Отсюда А2 + В2 = 0, т.е. А = В = 0, что противоречит условию. Итак, вектор
. Отсюда А2 + В2 = 0, т.е. А = В = 0, что противоречит условию. Итак, вектор 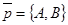 не параллелен прямой (рис.45).
не параллелен прямой (рис.45).
Рассмотрим множество всех точек плоскости, не лежащих на прямой l. Пусть М – любая из них. Пусть  параллелен
параллелен 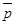 , где N Î l. Тогда
, где N Î l. Тогда 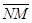 =
= 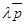 . При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор
. При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор 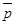 . Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l. Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той, в сторону которой направлен вектор
. Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l. Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той, в сторону которой направлен вектор 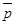 . Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.
. Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.
Рис. 45 Рис. 43 Рис. 44
27. Пучок а) параллельных прямых; б) пересекающихся прямых.
Определение 24. Пучком прямых на плоскости называется множество всех прямых этой плоскости, проходящих через одну точку. Эта точка называется центром пучка.
Пучок можно задать двумя способами: центром и парой пересекающихся прямых.
I. Пучок задан центром.
Дано. R = 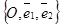 , С(х0, у0) – центр пучка (рис. 43).
, С(х0, у0) – центр пучка (рис. 43).
Найти условие, определяющее пучок.
Решение. Прямая l принадлежит пучку с центром С ó l ' С. При этом направляющим вектором может быть любой ненулевой вектор 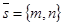 . Следовательно, l принадлежит пучку Û l:
. Следовательно, l принадлежит пучку Û l: 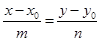 , где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением
, где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением 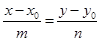 (36).
(36).
В уравнении (36) две пары переменных. Меняя m, n, мы будем получать все возможные прямые пучка. Если m, n зафиксированы, то зафиксирована прямая пучка. При этом, меняя х, у, мы будем получать все возможные точки на полученной прямой.
 2015-06-28
2015-06-28 1087
1087







