Пучком прямых на плоскости с центром в точке S называется множество всех прямых плоскости, проходящих через точку S.
Теорема 3 (о пучке прямых)
Пусть даны две прямые принадлежащие пучку прямых с центром в точке S
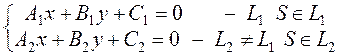 ,
,
Тогда 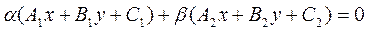 (32)
(32)
1. (32)- уравнение некоторой прямой пучка с центром в точке S.
2. Любая прямая пучка с центром в точке S имеет уравнение вида (32).
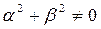
Д-во:
Перегруппируем левую часть уравнения (32)
1. 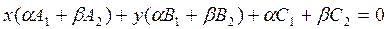 (32’)
(32’)
Необходимо определить степень уравнения. Уравнение (32’) может быть:
а) первой степени;
б) нулевой степени.
Нулевая степень будет тогда, когда 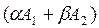 и
и 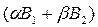 равны одновременно нулю:
равны одновременно нулю:
Пусть 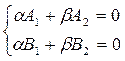 ,
, 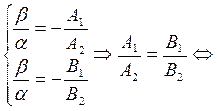 условие параллельности прямых
условие параллельности прямых 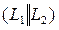 противоречит условиям теоремы
противоречит условиям теоремы 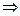 данное уравнение имеет первую степень.
данное уравнение имеет первую степень.
Пусть 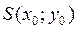 - центр пучка.
- центр пучка.
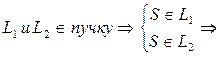 имеется система уравнений:
имеется система уравнений:
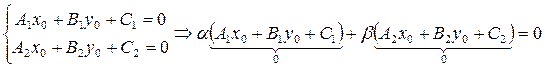
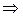 прямая (32) принадлежит пучку с центром в точке S.
прямая (32) принадлежит пучку с центром в точке S.
2. Пусть 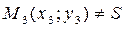 - произвольная точка плоскости, не лежащая ни на одной из данных прямых.
- произвольная точка плоскости, не лежащая ни на одной из данных прямых.
Рассмотрим прямую пучка L 3, проходящую через данную точку. Подставим координаты 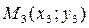 в (32). Найдем
в (32). Найдем 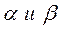 , при которых данное уравнение верно для
, при которых данное уравнение верно для 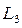 . Из (32):
. Из (32):
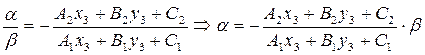
Подставим найденное 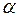 в (32):
в (32):
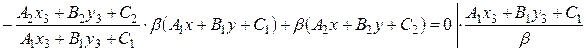
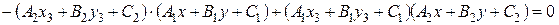
Подставим координаты точки S в уравнение: 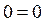 .
.
Подставим координаты точки 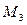 в уравнение (вместо
в уравнение (вместо 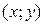 ):
): 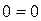 .
.
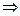 данное уравнение является уравнением прямой
данное уравнение является уравнением прямой 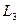 , т.к. данному уравнению удовлетворяют координаты точек S и
, т.к. данному уравнению удовлетворяют координаты точек S и 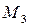 .
.
Теорема доказана
Пример:
1. Даны уравнения сторон треугольника:
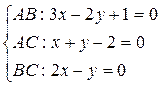
Определить, не проходят ли они через одну точку (т.е., действительно ли это треугольник).

2. Найти уравнение прямой, на которой лежит высота, опущенная из вершины A.

Решение:
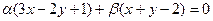
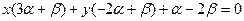
Найдем угловой коэффициент:
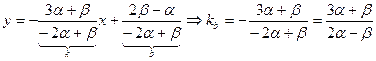
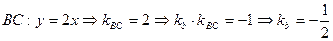 (условия перпендикулярных прямых).
(условия перпендикулярных прямых).
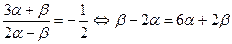
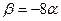
Подставляем 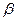 в уравнение пучка:
в уравнение пучка:
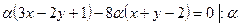
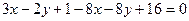
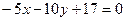
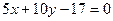
 2015-06-28
2015-06-28 411
411








