Ортонормированность дискретного базиса и зависимость погрешности интерполяции от степени гладкости функции

Прикладная математика. Вопрос 3.

Дискретное преобразование Фурье.

Ортонормированность дискретного базиса и зависимость погрешности интерполяции от степени гладкости функции.

1) Дискретное преобразование Фурье как задача интерполирования.

2) Построение интерполирующей функции.

3) Доказательство ортонормированности базиса.

4) Зависимость погрешности интерполяции от степени гладкости функции.

1. В линейной задаче интерполирования интерполирующая функция выбирается в виде линейной комбинации линейно независимого набора функций. В качестве такого набора можно использовать тригонометрические функции. Для краткости записи синусы и косинусы удобно комбинировать в эйлеровские экспоненты с мнимым показателем степени.

Интерполирующая функция, построенная на конечном комплексном экспоненциальном базисе, обычно называется дискретным рядом Фурье интерполируемой функции. Комплексные коэффициенты линейной комбинации экспонент называют дискретным Фурье-образом изучаемой функции (или коэффициентами дискретного Фурье-преобразования).

Дискретное преобразование Фурье применяется при решении многих прикладных задач. К ним относятся тригонометрическая интерполяция, вычисление свёртки функций, распознавание образов и многое другое.

2. Пусть имеется функция 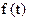. Нужно построить функцию 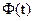, совпадающую на узлах с : .

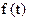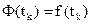Определим границы интервала интерполирования – [a, b]. Будем рассматривать такую 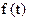, которая в силу периодичности имеет равные значения на краях интервала (для уменьшения погрешности).

Пусть будет М+1 внутренних узлов интерполяции (для удобства М - чётное). Сетка – равномерная:

Период Т интерполирующей функции: .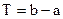

Шаг равномерной сетки: .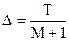

Узлы: .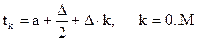

Введём равномерную сетку частот: 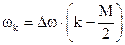, где 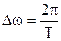- равномерная сетка частот. Существенно, что частоты расположены симметрично относительно нуля (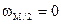) и принимают положительные и отрицательные значения (M/ 2 положительных и M/ 2 отрицательных значений).

Введём базисный набор функций: 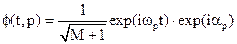, где .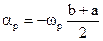

Значение базисных функций на узлах: 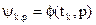, где 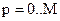. Получим матрицу W, где в каждый столбик записаны значения соответствующей базисной функции на узлах: .

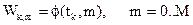Интерполирующую функцию строим как линейную комбинацию базисных функций: .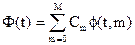

Система линейных уравнений для неизвестных коэффициентов 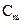имеет вид: 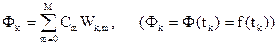. В векторном виде: 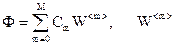- m-й столбец матрицы W. Тогда 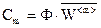(скалярное произведение) – так как базис ортонормированный, 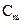являются координатами вектора и находятся единственным образом.

3) Проверим ортонормированность выбранного базиса:

4) Честно говоря, даже не знаю, что сказать по этому поводу. В конспекте про это ни слова.

В литературе есть следующее утверждение:

(a_N – коэффициент ряда Фурье, 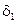- ошибка из-за отбрасывания далёких членов ряда, 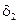- ошибка из-за погрешности коэффициентов).

Короче, общее соображение – чем более гладкая функция, тем меньше погрешность.