Операторный метод — это метод расчёта переходных процессов в электрических цепях, основанный на переносе расчёта переходного процесса из области функций действительной переменной (времени t) в область функций комплексного переменного (либо операторной переменной), в которойдифференциальные уравнения преобразуются в алгебраические.
Преобразование функций действительного переменного в операторную функцию производится с помощью методов операционного исчисления. Например, если в цепи имеется источник постоянной ЭДС 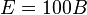 , то в операторной схеме замещения вместо неё будет операторная ЭДС
, то в операторной схеме замещения вместо неё будет операторная ЭДС 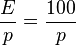 .
.
Последовательность расчёта операторным методом:
1. определяются независимые начальные условия;
2. вычерчивается операторная схема замещения, при этом электрические сопротивления заменяются эквивалентными операторными сопротивлениями, источники тока и источники ЭДС заменяются соответствующими операторными ЭДС, при этом следует учесть, что на месте реактивных сопротивлений помимо операторных сопротивлений появляются дополнительные операторные ЭДС;
3. находятся операторные функции токов и напряжений в цепи одним из методов расчёта электрической цепи с помощью решения обыкновенных алгебраических уравнений и их систем;
4. производится преобразование найденных операторных функций токов и напряжений в функцию действительного переменного с помощью методов операционного исчисления.
Анализ переходных процессов даже для относительно простых цепей зачастую представляет значительные сложности, т.к. требует решения дифференциальных уравнений. Задачу можно существенно упростить, если преобразовать уравнения, сделав их алгебраическими. Но в переходных процессах во всех функциях переменной величиной является время, поэтому для исключения производных требуется перейти к новой не зависящей от времени переменной. Такой переход для функции f (t) можно осуществить, например, с помощью преобразования Лапласа
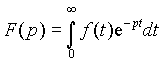 , ,
| (1) |
где p = a + jb - некоторое комплексное число, являющееся переменной функции F (p).
Функция времени f (t) называется оригиналом, а функция комплексной переменной F (p) - ее изображением.
Обратный переход от изображения к оригиналу может быть осуществлен с помощью обратного преобразования Лапласа
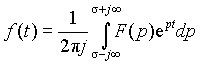 , ,
| (2) |
где интеграл вычисляется по прямой на плоскости комплексной переменной p, проходящей параллельно мнимой оси правее всех особых точек функции F (p).
Для большинства функций встречающихся в практических задачах существуют таблицы прямого и обратного преобразований и необходимость применения выражений (1) и (2) возникает крайне редко. Простейшие из этих преобразований приведены в таблице 1.
Таблица 1.
| Оригинал | Изображение | Оригинал | Изображение |
| C | C / p | t | 1/ p 2 |
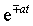
| 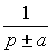
| 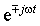
| 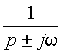
|
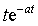
| 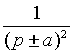
| 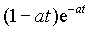
| 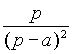
|
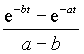
| 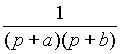
| 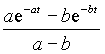
| 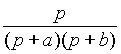
|
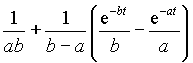
| 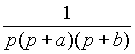
| 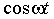
| 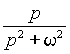
|
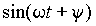
| 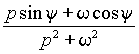
| 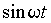
| 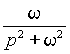
|
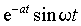
| 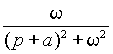
| 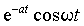
| 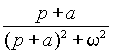
|
Переход от изображения к оригиналу функции может быть выполнен также с помощью формулы разложения.
Обычно изображение искомой величины F (p) получают (или его можно представить) в виде рациональной дроби
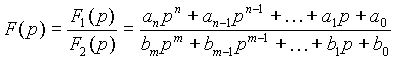 . .
| (3) |
Это выражение при условии, что n < m и знаменатель не имеет кратных корней, можно разложить на сумму простых дробей
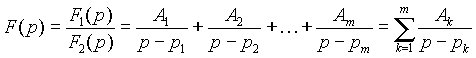 , ,
| (4) |
где pk - корни уравнения F 2(p) = 0.
Определим постоянные Ak. Для этого обе части выражения (4) умножим на (p - p 1)
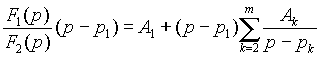
| (5) |
При p = p 1 правая часть выражения (5) равна A 1, а левая становится неопределенной, т.к. F 2(p 1) = 0. Раскрывая неопределенность по правилу Лопиталя, получим
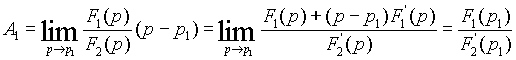
| (6) |
Следовательно, каждая постоянная в выражении (4) представляет собой отношение числителя исходной дроби к производной от знаменателя при подстановке в них соответствующего корня уравнения F 2(p) = 0. Отсюда
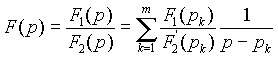 . .
| (7) |
Оригинал функции F (p) можно найти из выражения (7). В нем каждое слагаемое представляет некоторый постоянный коэффициент F 1(pk)/ F 2'(pk), умноженный на функцию 1/(p - pk), оригиналом которой (см. таблицу 1) является e pkt. Таким образом
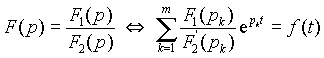 . .
| (8) |
Выражение (8) называется формулой разложения. Без доказательства отметим некоторые важные особенности.
- Если один из корней уравнения F 2(p) = 0 равен нулю, то это означает наличие в цепи источника постоянного тока. При этом знаменатель изображения имеет вид F 2(p 1) = pF 2(p 1) и формулу разложения можно представить как
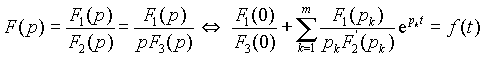 . .
| (9) |
- Если среди корней уравнения F 2(p) = 0 есть комплексно-сопряженные пары, то соответствующие им слагаемые выражения (8) также будут комплексно-сопряженными и в сумме дадут вещественное число. Поэтому для такой пары корней достаточно вычислить значение слагаемого только для одного корня, а затем взять его удвоенную вещественную часть.
- При наличии в цепи источника синусоидальной переменной ЭДС или тока с частотой w в спектре корней уравнения F 2(p) = 0 будет пара комплексно-сопряженных чисто мнимых корней ± jw, которая соответствует установившемуся значению.
| Оригинал | Изображение | Оригинал | Изображение |
| Af (t) | AF (p) | 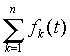
| 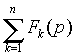
|
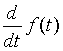
| 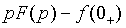
| 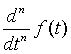
| 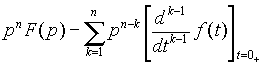
|
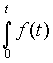
| 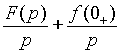
| 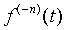
| 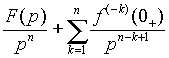
|
где 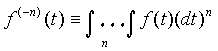 - интеграл n -го порядка.
- интеграл n -го порядка.
 2015-06-28
2015-06-28 658
658








