Найдите область сходимости ряда 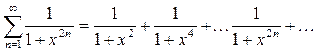 . Данный ряд определен для значений
. Данный ряд определен для значений 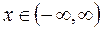 .
.
Если 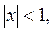 то
то 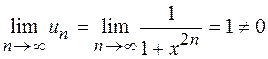 , ряд расходится, так как не выполняется необходимый признак сходимости ряда; если
, ряд расходится, так как не выполняется необходимый признак сходимости ряда; если 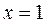 ряд
ряд 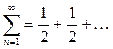 расходится; если
расходится; если 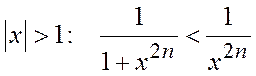 - бесконечно убывающая геометрическая прогрессия.
- бесконечно убывающая геометрическая прогрессия.
Сравнение данного ряда со сходящимся рядом 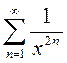 при
при 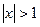 дает область сходимости исследуемого ряда
дает область сходимости исследуемого ряда 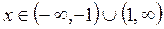 .
.
Определение 3. Функциональный ряд (1) называют абсолютно сходящимся в области D, если сходится ряд 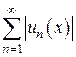 .
.
Пример 2. Найти область сходимости ряда 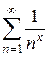 .
.
Решение. Обобщенный гармонический ряд 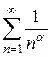 сходится, причем абсолютно при
сходится, причем абсолютно при 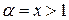 и расходится при
и расходится при 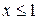 . Область сходимости данного ряда:
. Область сходимости данного ряда: 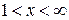 .
.
Пример 3. Найти область сходимости ряда 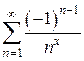 .
.
Решение. Для 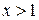 данный ряд сходится абсолютно (см.пример 1).
данный ряд сходится абсолютно (см.пример 1).
Для каждого 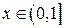 ряд сходится условно, как знакочередующийся ряд, удовлетворяющий признаку Лейбница. При
ряд сходится условно, как знакочередующийся ряд, удовлетворяющий признаку Лейбница. При 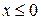 ряд расходится, т.к. не выполняется необходимый признак сходимости.
ряд расходится, т.к. не выполняется необходимый признак сходимости.
Т.о. областью сходимости является интервал 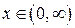 .
.
Замечание. Для определения области абсолютной сходимости функционального ряда (1) следует воспользоваться либо признаком Даламбера, либо признаком Коши. Именно, если 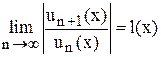 или
или 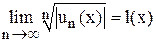 , то для определения области абсолютной сходимости ряда (1) следует решить функциональное неравенство
, то для определения области абсолютной сходимости ряда (1) следует решить функциональное неравенство 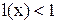 , а для определения области расходимости- функциональное неравенство -
, а для определения области расходимости- функциональное неравенство - 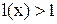 . При этом для изучения поведения ряда в граничных точках получаемой области, т.е. в точках, описываемых уравнением
. При этом для изучения поведения ряда в граничных точках получаемой области, т.е. в точках, описываемых уравнением 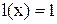 , требуется дополнительное исследование.
, требуется дополнительное исследование.
|
|
|
Определение 5. Сумму первых n членов ряда (1) 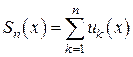 ,
,  называют n -й частичной суммой ряда (1).
называют n -й частичной суммой ряда (1).
Определение 6. Предел последовательности частичных сумм сходящегося в D функционального ряда 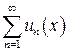 называют его суммой:
называют его суммой: 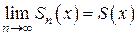 .
.
Определение 7. Функциональный ряд (1) называют равномерно сходящимся в области D к сумме 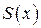 , если
, если 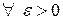
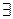 номер
номер 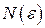 (зависящий только
(зависящий только 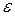 и не зависящий от
и не зависящий от 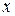 ) такой, что
) такой, что 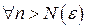 и
и 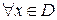 справедливо неравенство
справедливо неравенство 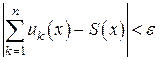 , т.е.
, т.е. 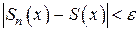 (т.е. в D последовательность его частичных сумм сходится равномерно).
(т.е. в D последовательность его частичных сумм сходится равномерно).
Замечание 2. Отметим еще раз принципиальное отличие равномерной сходимости от обычной: в случае обычной сходимости при выбранном значении ε для каждого 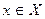 существует свой номер N, для которого при n > N выполняется неравенство:
существует свой номер N, для которого при n > N выполняется неравенство:
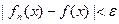 . При этом может оказаться, что подобрать для данного ε общий номер N, обеспечивающий выполнение этого неравенства для любого х, невозможно. В случае же равномерной сходимости такой номер N, общий для всех х, существует.
. При этом может оказаться, что подобрать для данного ε общий номер N, обеспечивающий выполнение этого неравенства для любого х, невозможно. В случае же равномерной сходимости такой номер N, общий для всех х, существует.
Геометрическая интерпретация равномерной сходимости (рис. 1).
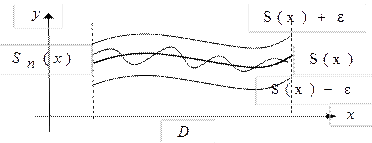
Если окружить график функции 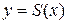 «
«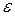 - полоской», определяемой соотношением
- полоской», определяемой соотношением 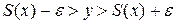 ,
, 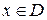 , то графики всех функций
, то графики всех функций  , начиная с достаточно большого значения
, начиная с достаточно большого значения 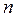 , целиком лежат в этой «
, целиком лежат в этой «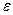 - полоске», окружающей график предельной функции
- полоске», окружающей график предельной функции 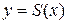 .
.
|
|
|
Теорема1. Критерий Коши равномерной сходимости ряда.
Для того чтобы функциональный ряд 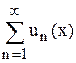 равномерно сходился в области D к некоторой сумме, необходимо и достаточно, чтобы
равномерно сходился в области D к некоторой сумме, необходимо и достаточно, чтобы 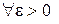 нашелся
нашелся 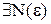 такой, что
такой, что 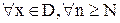 , для всех натуральных
, для всех натуральных 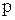 выполняется неравенство
выполняется неравенство 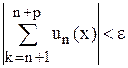 .
.
Достаточным признаком равномерной сходимости является признак Вейерштрасса (Карл Вейерштрасс (1815–1897) – немецкий математик).
Теорема2. Признак равномерной сходимости Вейерштрасса.
Если члены функционального ряда 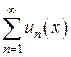 в некотором промежутке не превосходят по абсолютной величине соответствующих членов сходящегося числового ряда
в некотором промежутке не превосходят по абсолютной величине соответствующих членов сходящегося числового ряда 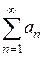 ,
, 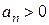 , т.е.
, т.е.
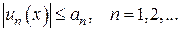 (2)
(2)
для всех 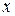 упомянутого промежутка, то ряд
упомянутого промежутка, то ряд 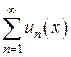 в данном промежутке сходится абсолютно и равномерно. Ряд
в данном промежутке сходится абсолютно и равномерно. Ряд 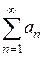 называется мажорирующим рядом или мажорантой.
называется мажорирующим рядом или мажорантой.
Краткая формулировка: функциональный ряд сходится равномерно на данном множестве, если его можно мажорировать на этом множестве сходящимся числовым рядом.
Доказательство:
Согласно критерию Коши для числового ряда 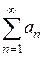 для
для 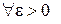 найдется
найдется 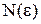
и для любого 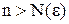 и
и 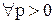 справедливо неравенство:
справедливо неравенство:
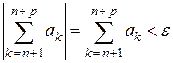 , (3)
, (3)
поэтому 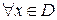 и
и 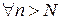 и
и 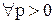 справедлива оценка
справедлива оценка
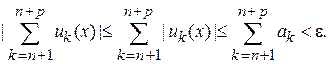 Следовательно, выполнен критерий Коши равномерной сходимости ряда, и ряд
Следовательно, выполнен критерий Коши равномерной сходимости ряда, и ряд 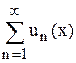
 сходится в области D равномерно. Теорема доказана.
сходится в области D равномерно. Теорема доказана.
Пример 4. Най ти область равномерной сходимости 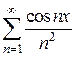 .
.
Решение. Для 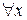
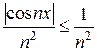 , сходящийся ряд
, сходящийся ряд 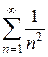 является мажорантой данного функционального ряда. По признаку Вейерштрасса данный функциональный ряд сходится равномерно на всей числовой оси.
является мажорантой данного функционального ряда. По признаку Вейерштрасса данный функциональный ряд сходится равномерно на всей числовой оси.
Пример 5. Доказать равномерную сходимость функционального ряда 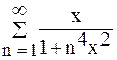 . Решение.
. Решение.  . Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить
. Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить 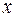 , при котором общий член ряда будет максимальным.
, при котором общий член ряда будет максимальным.
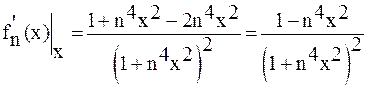 .
.
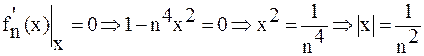 .
.
Тогда 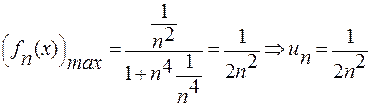 .
.
Полученный числовой ряд сходится, значит, функциональный ряд сходится равномерно согласно признаку Вейерштрасса.
Свойства равномерно сходящихся рядов:
1. Теорема3 (О непрерывности суммы ряда). Если члены ряда 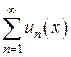 – непрерывные функции в точке
– непрерывные функции в точке 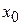 - внутренней точке области D и ряд в D сходится равномерно, то и его сумма
- внутренней точке области D и ряд в D сходится равномерно, то и его сумма 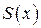 является непрерывной функцией в точке
является непрерывной функцией в точке 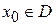 .
.
2. Теорема4 (О почленном интегрировании ряда).
Если функции 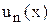 (n=1,2,3) непрерывны на отрезке [a;b] и ряд
(n=1,2,3) непрерывны на отрезке [a;b] и ряд 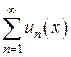 сходится на отрезке
сходится на отрезке 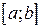 к
к 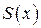 равномерно и каждая из функций
равномерно и каждая из функций 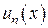
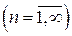 интегрируема на любом отрезке с концами в точках
интегрируема на любом отрезке с концами в точках 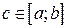 и
и 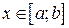 , то интегрируема
, то интегрируема 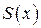
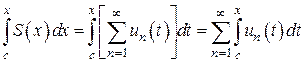 . (4)
. (4)
Пример6. Найти сумму ряда 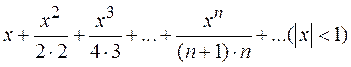 .
.
Решение: Присутствие вторых множителей в знаменателе, совпадающих с показателем степени 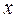 наводит на мысль, что ряд получен в результате почленного интегрирования. Очевидно, что ряд был такой:
наводит на мысль, что ряд получен в результате почленного интегрирования. Очевидно, что ряд был такой:
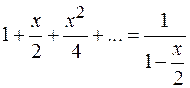 (*)
(*)
Члены этого ряда – это члены геометрической прогрессии со знаменателем 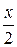 и первым членом, поэтому ряд сходится абсолютно при
и первым членом, поэтому ряд сходится абсолютно при 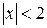 .
.
Почленно проинтегрировав ряд (*) получаем:
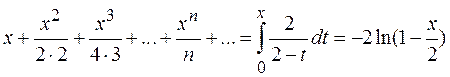
3. Теорема 5 (О почленном дифференцировании ряда).
Пусть ряд 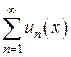 сходится к некоторой функции
сходится к некоторой функции 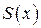 на отрезке
на отрезке 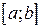 и каждая из функций
и каждая из функций 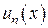
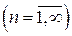 непрерывно дифференцируема на
непрерывно дифференцируема на 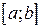 . Тогда, если ряд
. Тогда, если ряд 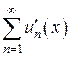 , сходится равномерно, то функция
, сходится равномерно, то функция 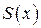 дифференцируема в каждой точке
дифференцируема в каждой точке 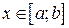 и справедливо равенство
и справедливо равенство 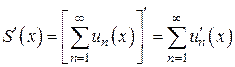 . (5)
. (5)
Пример7. Найти сумму ряда 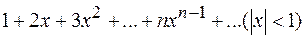 , продифференцировав почленно ряд
, продифференцировав почленно ряд 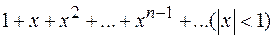 .
.
Решение: Воспользовавшись формулой суммы членов бесконечно убывающей геометрической прогрессии 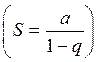 , получаем:
, получаем:
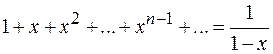 .
.
Остается продифференцировать полученное равенство:
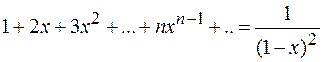
Пример8. Найти сумму ряда 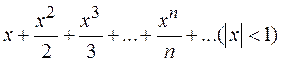 .
.
Решение: Продифференцировав почленно заданный ряд и найдем его сумму по формуле 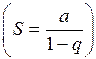 , где
, где 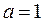 и
и 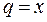 получим
получим
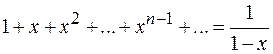
Проинтегрировав затем в пределах от 0 до х находим
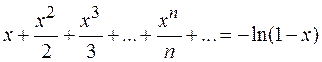
 2015-06-24
2015-06-24 3294
3294







