1. Вычислить 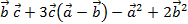 , если:
, если: 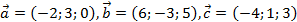 .
.
Решение:
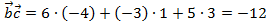 ,
,
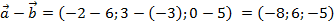 ,
,
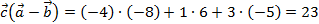 ,
,
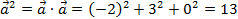 ,
,
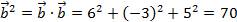 ,
,
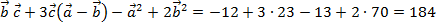
Ответ: 184.
2. Выяснить являются ли векторы 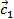 и
и 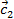 , построенные по векторам
, построенные по векторам 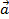 и
и 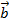 коллинеарными или ортогональными:
коллинеарными или ортогональными: 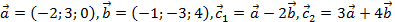 .
.
Решение:
1) 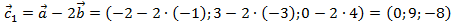 ,
,
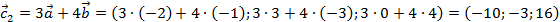 .
.
2) Т.к. 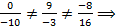
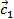 и
и 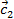 не являются коллинеарными.
не являются коллинеарными.
3) Т.к. 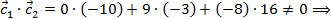
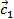 и
и 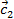 не являются ортогональными.
не являются ортогональными.
Ответ: 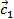 и
и 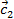 не являются коллинеарными;
не являются коллинеарными; 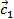 и
и 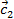 не являются ортогональными.
не являются ортогональными.
3. Даны A 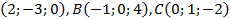 . Найти: 1) координаты векторов
. Найти: 1) координаты векторов 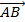 ,
, 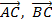 ,
,
2) длины векторов 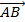 ,
, 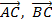 ,
,
3) косинусы углов между векторами 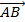 и
и 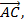
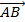 и
и 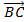 ,
, 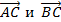 ,
,
4) определить вид треугольника ABC (остроугольный, тупоугольный, прямоугольный),
5) площадь треугольника ABC,
6) высоту треугольника ABC, проведенную из вершины С к стороне AB.
Решение:
1) Вычислим координаты векторов: 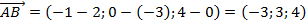 ,
,
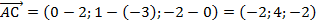 ,
,
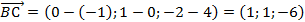 .
.
2) Найдем длины векторов: 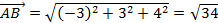 ,
,
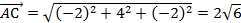 ,
, 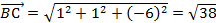 .
.
3) Найдем косинусы углов:
между векторами 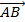 и
и 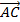 :
: 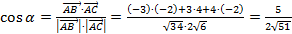 ,
,
между векторами 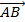 и
и 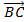 :
: 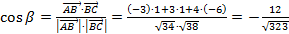 ,
,
между векторами 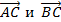 :
: 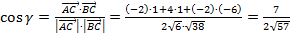 .
.
4) определить вид треугольника ABC:
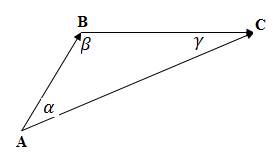
Рис.1
т.к. 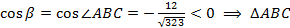 – тупоугольный (см. рис.1).
– тупоугольный (см. рис.1).
5) Найдем площадь 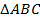 :
: 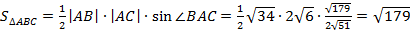 .
.
Замечание: 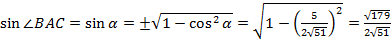 .
.
6) Найдем высоту треугольника ABC, проведенную из вершины С к стороне AB. Для этого построим ее (см. рис. 2, из вершины С проводим перпендикуляр СК на продолжение стороны АВ).
|
|
|
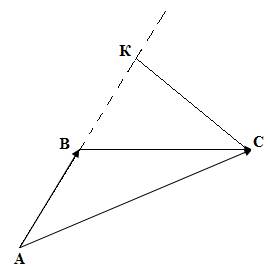
Рис.2
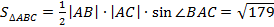 = или
= или 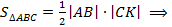
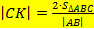 =
=
Ответ: 1) 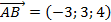 ,
, 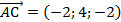 ,
, 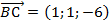 ; 2)
; 2) 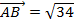 ,
, 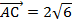 ,
, 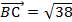 ; 3) между
; 3) между 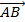 и
и 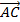 :
: 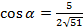 , между
, между 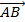 и
и 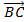 :
: 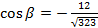 , между
, между 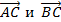 :
: 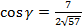 ; 4) тупоугольный; 5)
; 4) тупоугольный; 5) 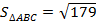 , 6).
, 6).
4. Даны 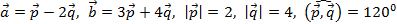 .
.
Найти: 1) длины векторов 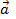 и
и 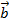 ,
,
2) косинус угла между векторами 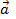 и
и 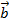 ,
,
3) площадь параллелограмма, построенного на векторах 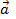 и
и 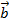 ,
,
4) площадь треугольника, построенного на векторах 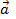 и
и 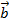 .
.
Решение:
1) Найдем длины векторов 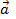 и
и 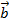 :
:
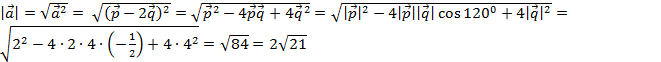 ,
,
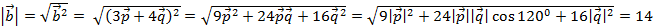 .
.
2) Найдем косинус угла между векторами 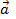 и
и 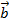 (см. рис.3) по формуле:
(см. рис.3) по формуле: 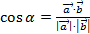 .
.
Найдем 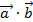 :
:
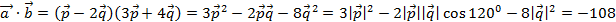 .
.
Тогда 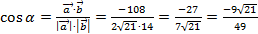 .
.
Т.к. 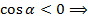 угол между векторами тупой (см. рис.3).
угол между векторами тупой (см. рис.3).
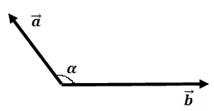
Рис.3
3) Найдем площадь параллелограмма, построенного на векторах 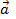 и
и 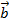 (см. рис.4) по формуле:
(см. рис.4) по формуле: 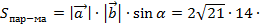 =
=
Замечание: 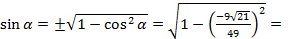 .
.
Рис.4
4) Найдем площадь треугольника, построенного на векторах 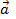 и
и 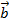 (см. рис.5) по формуле:
(см. рис.5) по формуле: 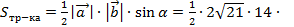 =
=
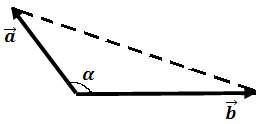
Рис.5
Ответ: 1) 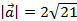 ,
, 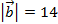 ; 2)
; 2) 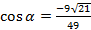 ; 3)
; 3) 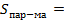 ; 4)
; 4) 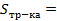
5. Компланарны ли векторы 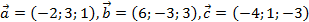 .
.
Решение: Воспользуемся определением компланарности трех векторов. Для этого найдем их смешанное произведение: 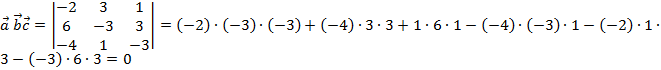 .
.
Т.к. смешанное произведение трех векторов равно нулю, следовательно, эти вектора компланарны.
Замечание: Нетрудно заметить, что элементы третьего столбца это суммы элементов первого и второго столбцов по соответствующим строкам, следовательно, по свойству определителей данный определитель равен нулю.
Ответ: компланарны.
6. Проверить являются ли векторы 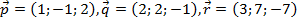 некомпланарными и найти разложение вектора
некомпланарными и найти разложение вектора 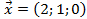 по векторам
по векторам 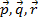 .
.
Решение:
1) Проверим являются ли векторы 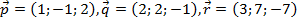 некомпланарными. Для этого найдем их смешанное произведение:
некомпланарными. Для этого найдем их смешанное произведение: 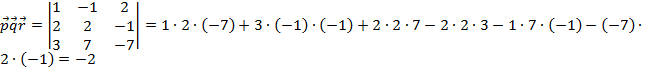 .
.
Т.к. смешанное произведение трех векторов не равно нулю, следовательно, эти вектора некомпланарны.
2) Любой вектор 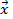 в пространстве можно единственным образом разложить по трем некомпланарным векторам
в пространстве можно единственным образом разложить по трем некомпланарным векторам 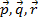 , т.е.
, т.е. 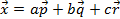 . Согласно последнему равенству составляем систему линейных уравнений по координатам:
. Согласно последнему равенству составляем систему линейных уравнений по координатам:
|
|
|
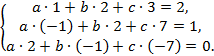
Полученную систему можно решить любым из методов, рассмотренных в теме «Системы линейных алгебраических уравнений». Воспользуемся методом Гаусса. Для этого составим матрицу коэффициентов 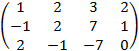 и приведем ее к квазитреугольному виду. Прибавляем элементы первой строки к соответствующим элементам второй строки:
и приведем ее к квазитреугольному виду. Прибавляем элементы первой строки к соответствующим элементам второй строки: 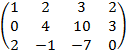 . Умножаем элементы первой строки на «
. Умножаем элементы первой строки на «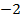 » и прибавляем к соответствующим элементам третьей строки:
» и прибавляем к соответствующим элементам третьей строки: 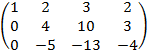 . Умножаем элементы второй строки на «
. Умножаем элементы второй строки на «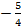 » и прибавляем к соответствующим элементам третьей строки:
» и прибавляем к соответствующим элементам третьей строки: 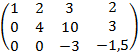 . Получили квазитреугольный вид, возвращаемся к системе:
. Получили квазитреугольный вид, возвращаемся к системе:
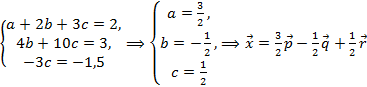 – искомое разложение.
– искомое разложение.
Ответ: 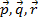 некомпланарны,
некомпланарны, 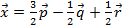 .
.
7. Проверить лежат ли точки 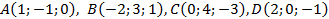 в одной плоскости.
в одной плоскости.
Решение:
Если точки 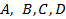 лежат в одной плоскости, то три вектора
лежат в одной плоскости, то три вектора 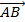 ,
, 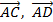 будут компланарны, и наоборот, если точки
будут компланарны, и наоборот, если точки 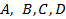 не лежат в одной плоскости, то три вектора
не лежат в одной плоскости, то три вектора 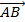 ,
, 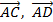 будут некомпланарны.
будут некомпланарны.
Найдем координаты векторов 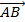 ,
, 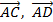 :
:
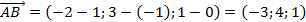 ,
,
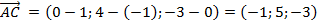
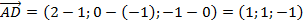 .
.
Проверим являются ли векторы 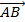 ,
, 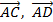 компланарными. Для этого найдем их смешанное произведение:
компланарными. Для этого найдем их смешанное произведение: 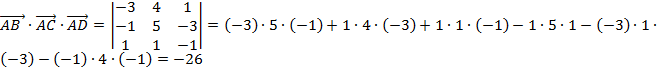 .
.
Т.к. смешанное произведение трех векторов не равно нулю, следовательно, эти вектора некомпланарны, а, следовательно, точки 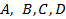 не лежат в одной плоскости.
не лежат в одной плоскости.
Ответ: точки 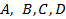 не лежат в одной плоскости.
не лежат в одной плоскости.
 2015-06-28
2015-06-28 930
930







