Отношение эквивалентности

Чаще всего рассматриваются отношения, обладающие сразу несколькими свойствами. Им присвоены определённые названия. Чаще всего встречаются и применяются отношения эквивалентности и порядка.

Рефлексивное симметричное транзитивное отношение.

Обозначается разными знаками: ≈, ≡, ~ – а также =.

Классом эквивалентности [x]_~ элемента х по отношению ~ на множестве А называется множество элементов y, т.ч. y~x. [x]_~ = {y|y 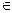A & y~x}.

Лемма 1. 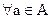[a]≠Ø. – Для любого элемента класс эквивалентности не пуст.

Лемма 2. a~b → [a]=[b]. – Классы эквивалентности эквивалентных элементов совпадают.

Пусть a~b. Тогда x 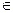[a] означает х~a & a~b → х~b (транзитивность) → x 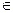[b].

Обратное включение доказывается аналогично с использованием условия симметричности a~b.

Лемма 3. ⌐a~b → [a] ∩ [b] = Ø.

Доказательство от противного: предположим, что существует элемент сÎ [a]∩[b]. Тогда этот элемент с~а&c~b. Следовательно, по свойству транзитивности и а~b – противоречие.

Следствием доказанных лемм является

Теорема. Всякое отношение эквивалентности на множестве А определяет разбиение множества А на непересекающиеся классы эквивалентности. Обратно, любое разбиение множества А задаёт на нём отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения множества А.

Проверка обратного утверждения: отношение включения a~b, если a,b 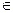А_i рефлексивно, симметрично и транзитивно.

Таким образом, существует взаимнооднозначное соответствие между разбиениями и отношением эквивалентности.

Если R – отношение эквивалентности на множестве А, то множество классов эквивалентности называется фактор-множеством множества А по отношению R и обозначается:

A/R={[x]_~|x Î A}, A/R Í 2^A

Пример. На множестве целых чисел Z определим отношение равенства по модулю k, k 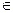N. Положим x=y(mod k), если x-e делится на k. Проверим, что это есть отношение эквивалентности: i) для любого целого числа m, m–m=0 – делится на k; ii) если m–n делится на k, то и n-m делится на k; iii) если m-n делится на k и n–p делится на k, то и сумма (m–n)+(n–p)=m–p – делится на k.

Равенство по модулю k означает, что при делении на k числа имеют одинаковые остатки: a=km+r. Поскольку остатков ровно k: 0, 1, 2, …, k–1, получаем ровно k попарно различных классов эквивалентности по данному отношению: [0], [1], …, [k–1]. [r] – класс всех целых чисел вида r+nk. Таким образом, мы построили фактор-множество Z/mod(k) и установили взаимнооднозначное соответствие между ним и множеством Z_k, состоящим из чисел {0, 1, …, k-1}. Подчеркнём, что это не отождествление, так как каждый класс состоит из бесконечного числа элементов.

Пример. На множестве действительных чисел R определим отношение x=y(mod(1)) = дробная часть числа x. Классы эквивалентности числа вида x=n+r, n – целое, r 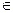[0,1); R/(mod(1))↔[0,1).

Помимо разбиений, существуют другие способы построения отношения эквивалентности.

Теорема. Пусть f: A→B – произвольная функция (отображение), т.е. бинарное отношение на множествах А и В, функциональное по второму аргументу). Тогда отношение R_f ={(x,y)| f(x)=f(y)} является отношением эквивалентности на множестве А. При этом существует биекция

φ: A/R_f → Im f.

ƒ Из определения R_f непосредственно следуют его рефлексивность, симметричность и транзитивность. Зададим отображение φ фактор-множества A/R_f в Im f следующим образом: φ([x]_R)=f(x).

Из способа задания отношения R_f следует, что отношение определено корректно, т.е. каждому классу эквивалентности поставлен в соответствие единственный элемент y 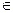Im f.

Докажем, что φ – биекция, для чего убедимся в том, что это инъекция и сюръекция одновременно. Пусть классы эквивалентности [x] и [y] не совпадают. В силу предыдущей теоремы это означает, что они не пересекаются, т.е. x ~ y. Из определения R_f следует, что в таком случае f(x)≠f(y) – таким образом, φ – инъекция. Если же элемент u 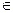Im f, то 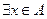, т.ч. u=f(x)= φ([x]_R), т.е. это сюръекция фактор-множества A/R_f. на множество Im f=f(A). ‚

Таким образом, существует тесная связь между отображениями, отношениями эквивалентности и разбиениями, которую можно изобразить графически в виде треугольника: