Матроиды

В основе решения задачи о минимальном остове лежит алгоритм, называемый «жадным»: из некоторого фиксированного множества сначала выбираются наиболее «лакомые» куски. В программистском фольклоре один из вариантов алгоритма имеет название «задачи о рюкзаке».

Вор забрался в магазин. Ему необходимо забрать самые ценные вещи, но при этом всё набранное должно поместиться в рюкзак (по весу Ú по объёму).

Сортируем все предметы по их стоимости (по убывающей). Берём первый предмет – если он помещается в рюкзак, кладём его; если нет – переходим к следующему. Так поступаем до тех пор, пока не дойдём до последнего по стоимости предмета.

Очевидно, что данный алгоритм является весьма эффективным, линейным по числу предметов (если не учитывать первоначальную сортировку и проверку на вместимость).

Формулировка Е ” 2^Е ” E Ì 2^Е; W: E#R₊;

задачи Найти XÍE & W(X) = max W(Y)|_YÍE.

Задача о контейнерах. Есть набор контейнеров и грузов – коробок. Требуется поместить коробки в контейнеры.

Жадный алгоритм даёт также приближённое решение задачи коммивояжёра – но, как правило, последний тур при этом оказывается слишком дорогим – в конце приходится платить за проявленную в начале пути жадность.

Возникает вопрос: в каких случаях жадный алгоритм действительно решает поставленную задачу? Когда выгодно быть жадным?

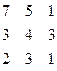
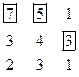
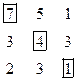
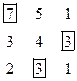
Рассмотрим следующие задачи.

1. Выбрать по одному элементу из каждого столбца так, чтобы их сумма была максимальной. Жадный алгоритм даёт точное решение.

2. Выбрать по одному элементу из каждого столбца и из каждой строки так, чтобы их сумма была максимальной. Жадный алгоритм даёт решение в 3-ей колонке. Точное решение выписано в 4-й колонке.

Матроиды. В силу необычайной эффективности (О(n)) жадного алгоритма естественно стремление применять его как можно чаще. Но когда он работает правильно? Установлено, что достаточное условие применимости жадного алгоритма – множество должно быть матроидом. (Это не значит, что жадный алгоритм не может давать точного решения и в других случаях.)

Матроидом называется пара M = <E, E>, где EÍ2Е, Е ¹ Æ– непустое множество. Элементы семейства подмножеств E называются независимыми.

Аксиомы матроида:

М₁. ÆÎE.— Эта аксиома гарантирует непустоту матроида.

М₂. АÎE&BÍA ”BÎE — свойство «наследования».

M₃. A, B Î E & |B| = |A| + 1 ” $ e ÎB\A: AÇ{ e } Î E — свойство замены.

Примером матроида может служить множество линейно независимых векторов линейного пространства. — Собственно, понятие матроида и возникло при изучении линейно независимых множеств векторов. Аксиомы проверяются элементарно. Матричный матроид.

Другим примером является множество всех лесных подграфов некоторого графа. Для проверки третьей аксиомы следует установить, что в б о льшем лесе всегда найдётся ребро, не дающее цикл при объединении с меньшим лесом. Графовый матроид. Матроид трансверсалей.