Основания Геометрии

В основе любых доказательств лежат некоторые «основополагающие положения», принимаемые без доказательств. В математике они называются аксиомами.

К системе аксиом, из которых потом, по правилам математической логики, выводятся новые утверждения, называемые теоремами, предъявляются следующие требования:

1. Непротиворечивость. Недопустимо, чтобы по правилам логики из одной и той же системы аксиом могло быть выведено утверждение А и его отрицание ùА.
2. Независимость. Никакая из аксиом системы не должна выводиться из остальных аксиом (иначе она бы называлась теоремой, а не аксиомой).
3. Полнота. Хорошо бы, чтобы все утверждения теории в рамках данной системы аксиом выводились бы или опровергались (т.е., мы могли бы доказывать либо утверждение А, либо его отрицание ùА). Последнее пожелание, однако, оказывается, далеко не всегда возможным выполнить, что показал (в отношении арифметики) немецкий математик Курт Гёдель перед второй мировой войной.

С геометрией, к изучению которой мы сейчас приступаем, дело как раз в этом отношении обстоит лучше, хотя система аксиом здесь намного сложнее, чем в арифметике натуральных чисел.

Помимо аксиом и теорем имеются ещё определяемые и неопределяемые понятия.

Как явствует из самих их названий, первым даются определения, в которых используются вторые (и уже ранее определённые понятия), а последним определения не даются, они считаются первоначальными, исходными.

В качестве первых неопределяемых понятий выступят точки, обозначаемые заглавными латинскими буквами, прямые, обозначаемые строчными латинскими буквами и плоскости, обозначаемые строчными греческими буквами.

Под любыми парами, тройками и т.д. точек, прямых, плоскостей понимаются всегда различные точки, прямые, плоскости.

Итак, следуя классическому труду [1], разобьём все аксиомы на группы по некоторым объединяющим их признакам.

Итак, первая группа аксиом – аксиомы инцидентности [1].

1. " пары точек А и В $! прямая инцидентная этим двум точкам.
2. На любой прямой существуют, по крайней мере, две точки (инцидентные ей).
3. Существуют три точки, не инцидентные (не принадлежащие) одной прямой.
4. " тройки точек А, В и С не инцидентных одной прямой, $! плоскость a, инцидентная каждой из этих точек.
5. Если две точки А и В прямой а инцидентны плоскости a, то и все точки прямой а инцидентны плоскости a.
6. Если две плоскости имеют одну общую точку, то они имеют, по крайней мере, ещё одну общую точку.
7. Существуют четыре точки, не инцидентные (не принадлежащие) одной плоскости.

Упражнение 1. Выведите из этих аксиом (докажите) следующие теоремы:

a) Две прямые, инцидентные одной плоскости не могут иметь более одной общей точки (т.е., могут не иметь ни одной или одну);

b) Две плоскости могут либо не иметь общих точек, либо иметь общую прямую и тогда никаких других общих точек, кроме точек этой прямой, они иметь не могут;

c) Плоскость и не инцидентная ей прямая либо не имеют общих точек, либо имеют одну общую точку;

d) " прямой и не инцидентной ей точки $! инцидентная им плоскость;

e) " пары прямых, имеющих общую точку, $! инцидентная им плоскость.

Вторая группа аксиом – аксиомы порядка.

Неопределяемым, первичным понятием выступает здесь слово «между».

2.1. Пусть точки А, В и С инцидентны одной прямой. Тогда, если В лежит между А и С, то В также лежит между С и А (отношение находиться «между» симметрично по отношению к А и С)

2.2. " точек А и С на прямой АС $ точка В такая, что С лежит между А и В.

2.3. " тройки точек А, В и С, инцидентных одной прямой, не более одной из них лежит между двумя другими[2].

А вот, наконец, и первые определяемые понятия.

Def. Пару точек (А,В) назовём отрезком АВ. Отрезок у нас пока что неориентированный, т.е пара (В,А) определяет тот же отрезок, ВА=АВ. Назовём точками отрезка АВ точки, лежащие между А и В. Другое их название – точки, расположенные внутри отрезка АВ. Сами точки А и В называются концами отрезка АВ. Остальные точки прямой АВ называются лежащими вне отрезка АВ.

Аксиоматика геометрии складывалась медленно и трудно, на протяжении многих веков, начиная с «Начал» Евклида и даже задолго до него, в работах египтян, опыт которых унаследовали греки. По существу, к современному состоянию аксиоматика геометрии трудами многих математиков подошла лишь к концу XIX века.

Оказалось, что при внимательном исследовании доказательств геометрических теорем на плоскости явно или неявно, помимо всех вышеназванных, используются утверждения, эквивалентные следующей аксиоме, сформулированной в таком виде в 1882 году Пашем (Pasch, Vorlesungen über neure Geometrie).

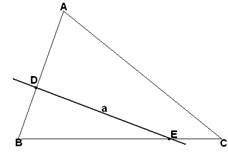2.4. Пусть А, В, С – тройка точек не инцидентных одной прямой, а – прямая в плоскости АВС, не инцидентная ни одной из них. Тогда если а инцидентна одной из точек отрезка АВ, то она также должна быть инцидентна одной из точек отрезка АС, или одной из точек отрезка ВС. Другими словами, если она входит в треугольник АВС через одну из его сторон, то она должна выйти через другую.

Упражнение 2*.

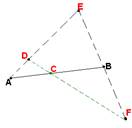
" точек А и B на прямой АB $ точка C такая, что C лежит между А и B. (Hint: use axioms #3, twice #2.2 and 2.4. consequently. Picture below illustrates the process of proving)

Упражнение 3*.

Пусть А, В, С – тройка точек, инцидентных одной прямой. Докажите, что тогда одна из них лежит между двумя другими.

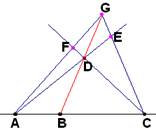(Let AÏBC and CÏAB. Then we are to prove BÎAC. Firstly, take DÏa=ABC to continue constructions on a plane. On BD find G| DÎBG. Let E=CGÇAD and F=CDÇAG. Considering corresponding triangles, prove, that EÎCG and, afterwards, that FÎAG. Apply 2.4. again to show, that DÎAE and, finally, show that BÎAC)

Теперь мы дополним (уточним) аксиому Паша.

Упражнение 4*.

Пусть А, В, С – тройка точек не инцидентных одной прямой, а – прямая в плоскости АВС, не инцидентная ни одной из них. Тогда если а инцидентна одной из точек отрезка АВ, то она также должна быть инцидентна либо одной из точек отрезка АС, либо одной из точек отрезка ВС, но не обоим одновременно. Другими словами, прямая не может пересечь все три стороны треугольника в его внутренних точках.

Доказательство можно вести «от противного», предположив, что эта (невозможная) ситуация как раз реализовалась.

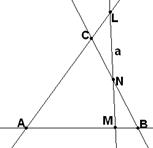Итак, прямая а=MNL пересекает все три стороны треугольника АВС во внутренних точках отрезков MÎAB, NÎBC и LÎAC. Докажите невозможность этого, придя к противоречию.

(Hint: one of three points M, N and L lies between two others, (why?) let it be N. B lies outside segment AM (why?); consider line a¢=BC and triangle ALM. Show, that a¢ÇAL in CÎAL and come to contradiction)

Упражнение 5*.

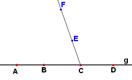
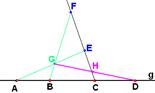Даны прямая g и на ней 4 точки А, B, C и D, причём В лежит между А и С, а С – между В и D. Докажите, что тогда обе точки В и С лежат также и между А и D.

(Again, firstly take some point E outside line g. Let F be point on line CE| EÎCF. Prove, that AEÇBF in some point G between B and F. GÎBF and GÎAE. Prove, that line CFÇGD in HÎCE and HÎGD. Prove, that line EH intersects segment AD in its inner point C)

Упражнение 6*.

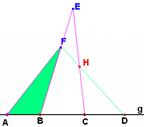
Пусть точка В лежит на отрезке АС, а точка С – на отрезке AD. Докажите, что тогда точка В также лежит на отрезке AD, а точка С лежит также и на отрезке ВD.

(Let FÏg, FÎBE. Prove, that CE does not intersect segment AF. Prove then, that CE does intersect segment FD in some point H. Prove then, that EH intersects BD)
Упражнение 7*.

Любые четыре точки на прямой можно так обозначить буквами А, B, C и D, чтобы при этом В лежала как между А и С, так и между А и D, а С лежала бы как между В и D, так и между А и D.
(Firstly take three of them, call them P, Q and R and let Q be in between P and R. For the last one, let it be S, there are 3 options: SÎPR, PÎSR, RÎPS. Beside that, either QÎPS, or SÎPQ or PÎQS. In fact, there are only 5 options for S; consider them separately and apply ex. 7 or 6).

Упражнение 8*.

Каково бы ни было конечное множество точек на прямой, их можно обозначить буквами А₁, А₂,…,A_n так, что А_i находится между А₁, А₂,…,A_i-1 с одной стороны и A_i+1, A_i+2,…,A_n с другой для всех i=2,3,…,n-1. Возможностей для выбора таких обозначений всего две: прямая и обратная. (Use induction, for n=4 theorem holds true. Prove, that there are two points A₁ and A_n, that all other n-2 points lie in between them. Start from two points, containing maximum of other points and use ex. #6)