9.1. Определение производной. Геометрический и механический смысл:
Определение:
Предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю произвольным образом, называется производной функции. Таким образом: 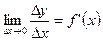 .
.
Обозначение: 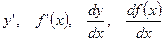 .
.
Геометрический смысл производной:
Производная функции 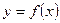 , вычисленная в т.
, вычисленная в т. 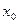 есть угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой
есть угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой 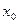 , т.е.
, т.е. 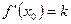 .
.
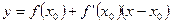 - уравнение касательной к графику функции
- уравнение касательной к графику функции 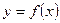 в точке
в точке
с абсциссой 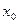 .
.
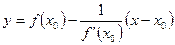 - уравнение нормали к графику функции
- уравнение нормали к графику функции 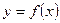 в точке
в точке
с абсциссой 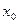 .
.
Механический смысл производной:
Производная от пути по времени при прямолинейном движении точки, есть истинная или мгновенная скорость движения 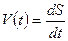 .
.
9.2. Таблица производных:
1. 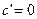 2.
2. 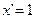 3.
3. 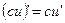 4.
4. 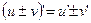 5.
5. 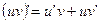 6.
6. 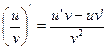 7.
7. 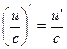 8.
8. 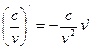 9.
9. 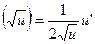 10.
10. 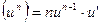 11.
11. 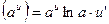 12.
12. 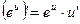 13.
13. 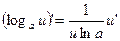  14.
14. 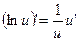
| 15. 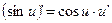 16.
16. 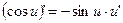 17.
17. 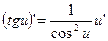 18.
18. 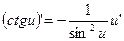 19.
19. 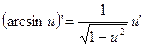 20.
20. 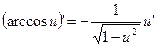 21.
21. 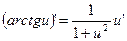 22.
22. 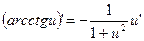 23.
23. 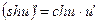 24.
24. 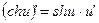 25.
25. 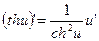 26.
26. 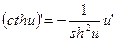
|
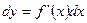 - формула нахождения дифференциала.
- формула нахождения дифференциала.
Геометрический смысл дифференциала: дифференциал функции 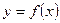 отнесенный к точке
отнесенный к точке 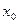 равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой
равен приращению ординаты касательной, проведенной к графику функции в точке с абсциссой 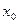 .
.
9.3. Логарифмическое дифференцирование:
Применяется для нахождения производной:
1. Степенно-показательной функции 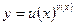
2. От произведений и частных, содержащих большое число сомножителей:
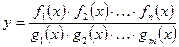
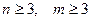 .
.
Алгоритм применения:
Пусть функция 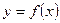 положительная и дифференцируема при всех рассматриваемых
положительная и дифференцируема при всех рассматриваемых  .
.
1) Логарифмируем заданное равенство 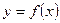 по основанию
по основанию 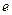 . Имеем:
. Имеем: 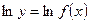 .
.
2) Дифференцируем полученное равенство по  , учитывая что
, учитывая что  - независимая переменная, а
- независимая переменная, а 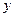 - функция
- функция  , тогда:
, тогда: 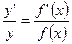 .
.
3) Результат дифференцирования разрешаем относительно 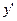 :
: 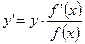 .
.
4) Заменяем в последнем равенстве 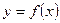 :
: 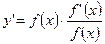 .
.
9.4. Дифференцирование функций, заданных неявно:
Пусть 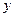 как функция
как функция  задана неявно, т.е.
задана неявно, т.е. 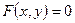
Алгоритм:
1) Дифференцируем заданное уравнение 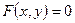 по
по  , учитывая, что
, учитывая, что  - независимая переменная,
- независимая переменная, 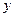 - ее функция.
- ее функция.
2) Результат дифференцирования разрешаем относительно искомой производной 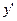 .
.
9.5. Дифференцирование функций, заданных параметрически:
Пусть 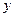 как функция
как функция  задана параметрически, т.е.
задана параметрически, т.е.
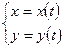 ,
, 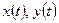 - дифференцируемы при всех рассматриваемых
- дифференцируемы при всех рассматриваемых 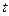 ,
, 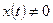 и
и 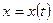
имеет обратную 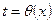 .
.
Тогда: 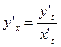
9.6. Производные высших порядков:
Определение:
Производной  - го порядка функции
- го порядка функции 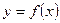 называется первая производная от
называется первая производная от
производной 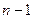 порядка:
порядка: 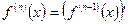 ,
, 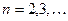
1) Пусть 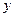 как функция
как функция  задана неявно, т.е.
задана неявно, т.е. 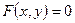 .
.
Для нахождения  - ой производной продифференцируем заданное равенство по
- ой производной продифференцируем заданное равенство по  последовательно
последовательно  раз. Результат последнего дифференцирования разрешаем относительно
раз. Результат последнего дифференцирования разрешаем относительно 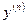 и представляем ее только в переменных
и представляем ее только в переменных  и
и 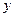 , для чего результаты всех промежуточных дифференцирований представлять только в переменных
, для чего результаты всех промежуточных дифференцирований представлять только в переменных  и
и 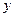 .
.
2) Пусть 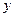 как функция
как функция  задана параметрически, т.е.
задана параметрически, т.е. 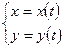
 ,
, 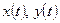 - дважды дифференцируемы,
- дважды дифференцируемы, 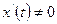 , функция
, функция 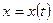 имеет обратную
имеет обратную 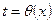 .
.
Тогда: 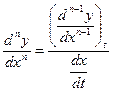 ,
, 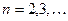
9.7. Раскрытие неопределенностей по правилу Лопиталя:
1) Если при 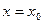 отношение двух функций
отношение двух функций 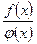 дает неопределенность
дает неопределенность 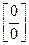 , то предел отношения этих функций можно заменить пределом отношения производных от этих функций:
, то предел отношения этих функций можно заменить пределом отношения производных от этих функций: 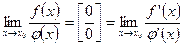
Замечания:
-Правило Лопиталя остается справедливым для раскрытия неопределенности 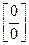 и при
и при 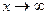 ;
;
-Правило Лопиталя можно применять несколько раз подряд, если отношение последовательных производных каждый раз дает неопределенность 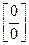 ;
;
-Правило Лопиталя применимо лишь в случае, когда существует конечный или бесконечный предел отношения производных, если этот предел не существует, то отсюда не следует, что не существует и предел отношения самих функций.
2) Если при 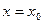 отношение двух функций
отношение двух функций 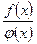 дает неопределенность
дает неопределенность 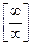 , то предел отношения этих функций можно заменить пределом отношения производных от этих функций:
, то предел отношения этих функций можно заменить пределом отношения производных от этих функций: 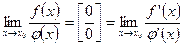 .
.
Все замечания, сделанные при раскрытии неопределенности 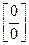 остаются справедливыми.
остаются справедливыми.
Таблица степени роста при 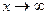
1. 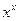
2. 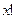
3. 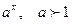
4. 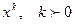 ,
, 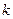 - рациональное
- рациональное
5. 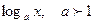
3) Неопределенности вида 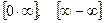 .
.
Такие неопределенности сводятся к неопределенностям вида 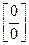 и
и 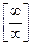 , для чего необходимо
, для чего необходимо 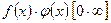 или
или 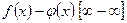 представить в виде единой дроби.
представить в виде единой дроби.
4) Неопределенности вида 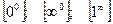 .
.
Такие неопределенности возникают при нахождении пределов от степенно-показательных функций 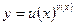 .
.
Один из способов раскрытия:
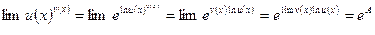 .
.
9.8. Формула Тейлора:
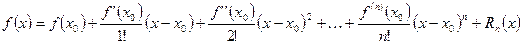 , где
, где
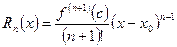 ,
, 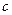 - некоторая точка окрестности
- некоторая точка окрестности 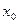 .
.
Формула Тейлора позволяет приближенно представлять функции в виде многочленов любой требуемой степени и определяет погрешность такого представления.
9.10. Общая схема исследования функции и построения ее графика:
1) Устанавливаем область определения 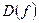 , точки разрыва, интервалы непрерывности.
, точки разрыва, интервалы непрерывности.
2) Исследуем функцию на четность, нечетность, периодичность.
3) Находим ВАС: 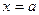 , где
, где 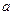 - такое значение аргумента при котором функция
- такое значение аргумента при котором функция  становится бесконечно большой
становится бесконечно большой
Находим НАС: 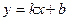 , где
, где 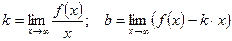 (если хотя бы один из пределов не существует или равен бесконечности, то график не имеет НАС).
(если хотя бы один из пределов не существует или равен бесконечности, то график не имеет НАС).
4) Определяем интервалы монотонности и экстремумы с помощью первой производной.
5) Находим интервалы вогнутости, выпуклости, точки перегиба с помощью второй производной.
6) Определяем точки пересечения графика с осями координат (если с осью 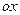 , то решаем уравнение
, то решаем уравнение 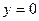 , если с осью
, если с осью 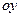 , то находим
, то находим 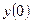 ).
).
7) Если график не имеет НАС, то исследуем поведение  при
при 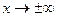 .
.
8) Строит график функции.
 2015-06-26
2015-06-26 779
779








