13.1. Основные понятия:
Определение:
Соответствие 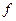 , при котором каждой паре числовых значений двух независимых друг от друга переменных величин
, при котором каждой паре числовых значений двух независимых друг от друга переменных величин  и
и 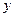 взятых из области их изменения отвечает одно и только одно числовое значение переменной величины
взятых из области их изменения отвечает одно и только одно числовое значение переменной величины 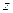 , называют числовой функцией двух переменных.
, называют числовой функцией двух переменных.
Обозначение: 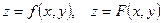 .
.
Здесь 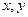 - аргументы (независимые переменные),
- аргументы (независимые переменные), 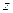 - зависимая переменная (функция).
- зависимая переменная (функция).
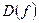 - область определения,
- область определения, 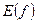 - область значений.
- область значений.
Определение:
Совокупность всех точек пространства, координаты которых удовлетворяют уравнению 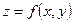 , называют графиком соответствующей функции.Обычно график функции
, называют графиком соответствующей функции.Обычно график функции 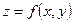 представляет собой поверхность, с которой любая прямая параллельная ось
представляет собой поверхность, с которой любая прямая параллельная ось 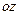 ,пересекается не более чем в одной точке.
,пересекается не более чем в одной точке.
Способы задания: табличный, графически, аналитически.
Определение:
Число А называется пределом функции 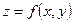 при стремлении точки
при стремлении точки 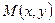 к точке
к точке 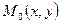 , если для любого
, если для любого 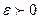 существует
существует 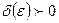 : для всех точек
: для всех точек 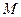 координаты которых удовлетворяют соотношениям
координаты которых удовлетворяют соотношениям 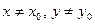 и
и 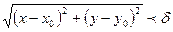 справедливо неравенство
справедливо неравенство 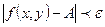 .
.
Обозначение: 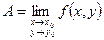 или
или 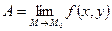 .
.
Этот предел существует тогда и только тогда, когда по каждому из направлений предел имеет одно и тоже значение.
Определение:
Функция 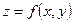 называется непрерывной в точке
называется непрерывной в точке 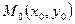 , если:
, если:
- она определена в точке 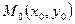 и ее окрестности;
и ее окрестности;
- в точке 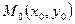 предел функции равен значению функции в этой точке
предел функции равен значению функции в этой точке 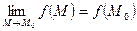 .
.
Определение:
Функция 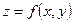 называется непрерывной на некотором множестве, если она непрерывна в каждой точке этого множества.
называется непрерывной на некотором множестве, если она непрерывна в каждой точке этого множества.
13.2. Частные производные:
Определение:
Частной производной функции 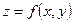 по
по  называется предел отношения частного приращения этой функции по
называется предел отношения частного приращения этой функции по  к приращению аргумента
к приращению аргумента 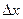 при условии, что
при условии, что 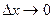 произвольным образом.
произвольным образом.
Т.о. 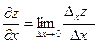 . Аналогично,
. Аналогично, 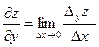 .
.
Чтобы найти частную производные по  функции
функции 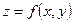 необходимо в выражении
необходимо в выражении 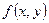 переменную
переменную 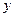 считать постоянной и дифференцировать при этом условии
считать постоянной и дифференцировать при этом условии 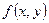 по
по  как функцию одной переменной. Аналогично, для нахождения частной производной по переменной
как функцию одной переменной. Аналогично, для нахождения частной производной по переменной 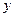 .
.
Геометрический смысл:
Пусть функция 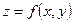 определена и непрерывна в некоторой области
определена и непрерывна в некоторой области 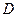 , тогда частной производной функции
, тогда частной производной функции 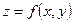 по
по  (по
(по 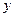 ) вычисленная в точке
) вычисленная в точке 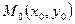 есть тангенс угла между осью
есть тангенс угла между осью 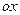
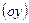 и касательной, проведенной в соответствующей точке поверхности к линии ее пересечения плоскостью
и касательной, проведенной в соответствующей точке поверхности к линии ее пересечения плоскостью 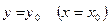 .
.
Определение:
Частной производной  - го порядка функции
- го порядка функции 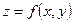 называется частная производная первого порядка по одной из переменных
называется частная производная первого порядка по одной из переменных  или
или 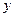 от частной производной
от частной производной 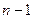 порядка
порядка 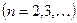 .
.
Теорема (о равенстве смешанных производных):
Если функция 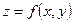 имеет всевозможные непрерывные частные производные до
имеет всевозможные непрерывные частные производные до 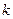 - го порядка включительно, то значения любой смешанной производной
- го порядка включительно, то значения любой смешанной производной 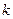 - порядка не зависит от того порядка, в котором для ее получения проводились последовательные дифференцирования по
- порядка не зависит от того порядка, в котором для ее получения проводились последовательные дифференцирования по  и по
и по 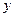 , но зависит от общего числа дифференцирований по каждому из аргументов.
, но зависит от общего числа дифференцирований по каждому из аргументов.
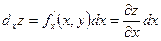 - формула нахождения частного дифференциала по
- формула нахождения частного дифференциала по  .
.
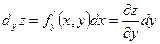 - формула нахождения частного дифференциала по
- формула нахождения частного дифференциала по 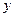 .
.
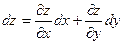 - формула нахождения полного дифференциала.
- формула нахождения полного дифференциала.
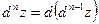 , где
, где 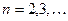
Теорема (признак полного дифференциала):
Если функции 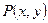 ,
, 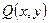 и их частные производные первого порядка по обоим переменным
и их частные производные первого порядка по обоим переменным  и
и 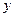 непрерывны в некоторой области
непрерывны в некоторой области 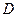 , то для того чтобы в этой области выражение
, то для того чтобы в этой области выражение 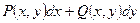 было полным дифференциалом некоторой функции
было полным дифференциалом некоторой функции 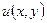 , необходимо и достаточно, чтобы в каждой точке этой области выполнялось равенство:
, необходимо и достаточно, чтобы в каждой точке этой области выполнялось равенство: 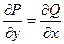 .
.
13.3. Дифференцирование сложных функций:
1. Общий случай:
Пусть 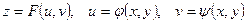 , тогда
, тогда
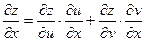 и
и 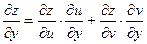 .
.
2. Полная производная:
Пусть 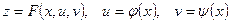 , тогда
, тогда
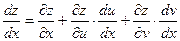 .
.
13.4. Дифференцирование неявных функций:
1. Неявная функция одной переменной: 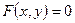 , тогда
, тогда
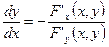 или
или 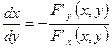 ;
;
- Неявная функция двух переменных:
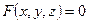 , тогда
, тогда
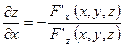 и
и 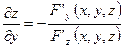 , если функция
, если функция 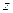 зависит от переменных
зависит от переменных  ,
, 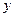 .
.
Имеем аналогичные формулы, если 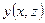 или
или 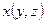 .
.
13.5. Касательная плоскость и нормаль к поверхности:
1) Если поверхность задана явно уравнением 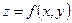 , то
, то
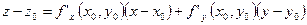 - уравнение касательной плоскости к этой поверхности в точке
- уравнение касательной плоскости к этой поверхности в точке 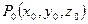
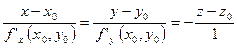 - уравнение нормали к этой поверхности в точке
- уравнение нормали к этой поверхности в точке 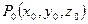 .
.
2) Если поверхность задана неявно уравнением 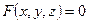 , то
, то
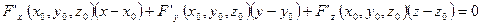 - уравнение касательной плоскости к этой поверхности в точке
- уравнение касательной плоскости к этой поверхности в точке 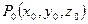 .
.
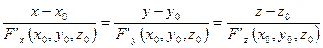 - уравнение нормали к этой поверхности в точке
- уравнение нормали к этой поверхности в точке 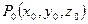 .
.
13.6. Экстремумы функции двух переменных:
Определение:
1)Точка, в которой хотя б одна из частных производных первого порядка функции 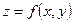 не существует или обе обращаются в нуль, называется критической точкой этой функции.
не существует или обе обращаются в нуль, называется критической точкой этой функции.
2) Точка, в которой обе частные производные первого порядка равны нулю, называется стационарной точкой.
Теорема (достаточный признак существования экстремума функции):
Если в стационарной точке 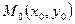 функция
функция 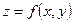 имеет всевозможные непрерывные частные производные второго порядка и если в этой точке:
имеет всевозможные непрерывные частные производные второго порядка и если в этой точке:
- 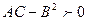 , то
, то 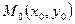 - точка экстремума и
- точка экстремума и 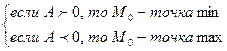 ;
;
- 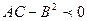 , то в точке
, то в точке 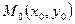 - экстремума нет;
- экстремума нет;
- 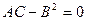 , неопределенный случай.
, неопределенный случай.
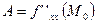 ;
; 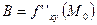 ;
; 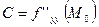
Правило нахождения экстремума функции 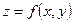 :
:
1) Определяем 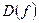 ;
;
2) Находим стационарные точки, лежащие строго внутри 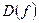 ;
;
3) Для каждой такой стационарной точки составляем выражение 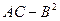 и с его помощью устанавливаем наличие в стационарной точке экстремума, а по знаку
и с его помощью устанавливаем наличие в стационарной точке экстремума, а по знаку  определяем его характер;
определяем его характер;
4) Вычисляем значение заданной функции в точке экстремума, тем самым получаем 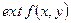 .
.
 2015-06-26
2015-06-26 1620
1620








