Существует легенда о наблюдении математика за блужданиями пьяного. Пьяный начинает свое движение от фонаря, расположенного в центре большой городской площади. Это обеспечивает равновероятность движения объекта в ту или иную сторону. Для контрольного примера, который позволил бы найти пройденное расстояние за n шагов, можно выбрать двузначные числа из таблицы. Тогда если первая цифра равна нулю или четна, то приращение по x равно +1, иначе -1. аналогично кодируется изменение координаты y. Пусть n=5. Из таблицы выбраны следующие числа:
| Шаг | Первая цифра | Вторая цифра | Координаты (x,y) |
| (-1,1) | |||
| (-2,0) | |||
| (-1,1) | |||
| (-2,2) | |||
| (-3,1) |
n=5, a=√2, s=√10
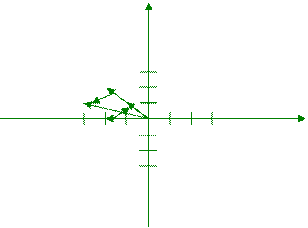 |
-1 -2 -3 1 2 3
В результате имитации получена аналитическая модель S=a√n, которая позволяет найти искомый параметр S без проведения экспериментов. a – средняя длина одного шага, n – количество шагов. При повторении имитационного эксперимента получаются разные оценки параметра S, которые затем усредняются. Чем больше опытов, тем точнее оценки.
Другой задачей моделирования равномерно распределенной величины является имитация бросания кубика (игральной кости). В результате имитации нужно получить n значений случайной величины x с законом распределения:
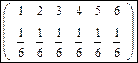
Для имитации x можно воспользоваться формулой x=a+[nγ], где a – начальное значение x из возможных, n – количество реализаций дискретной случайной величины, γ – псевдослучайное число, полученное из таблицы случайных чисел путем выделения 3 х -значного числа и умножения его на 10-3, […] – выделение целой части. γ представляет собой равномерно распределенные дроби в интервале от 0 до 1. Если n=10, то можно получить из таблицы случайных чисел 10 значений дробей: 0,865, 0,159, 0,079, 0,566, 0,155, 0,664, 0,345, 0,655, 0,812, 0,332.
x1=1+[6∙0,865]=1+5=6
x2=1+[6∙0,159]=1+0=1
x3=1+[6∙0,079]=1+0=1
x4=1+[6∙0,566]=1+3=4
x5=1+[6∙0,155]=1+0=1
x6=1+[6∙0,664]=1+3=4
x7=1+[6∙0,345]=1+2=3
x8=1+[6∙0,655]=1+3=4
x9=1+[6∙0,812]=1+4=5
x10=1+[6∙0,332]=1+1=2
Выборочный закон распределения: 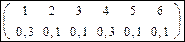
Он отличается от генеральной совокупности, так как n – мало.
Более сложные алгоритмы разыгрывания применяются для непрерывных случайных величин. Особенно сложно учитывать симметричность распределения. Поэтому наряду с методом Монте-Карло применяются другие методы разыгрывания (смотрите в учебнике Гмурмана). Можно разыграть вероятность (по F(x)), либо плотность вероятности (f(x)). Например:
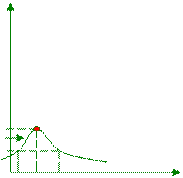 |
γ
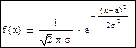 γ=f(x), x – по формуле:
γ=f(x), x – по формуле:
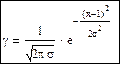
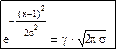
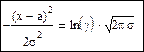
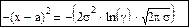
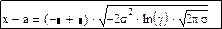
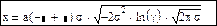
Для определения знака можно рассмотреть различные алгоритмы, в частности можно применить возведение -1 в степень k, где k – номер опыта.
Вариант блок-схемы получения нормально распределенных величин x с заданными параметрами распределения.
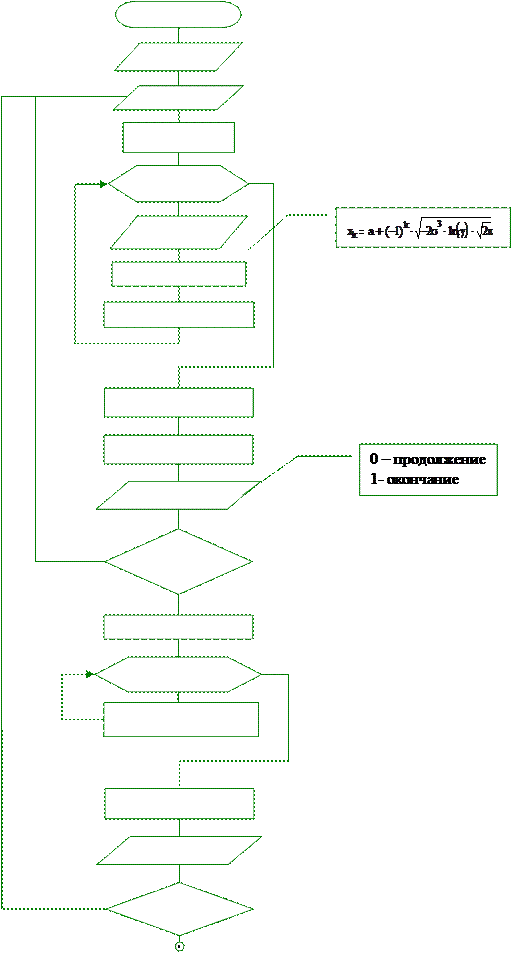
начало
a,b
N
S:=0
k:=1, N
γ
расчет k
S:=S+xk
A1:=S/N
A1
p(m/n)
+
p=0
S:=0
k:=1, N
S1:=S1+(xk-A1)2
σ1:=S1/N
p(m/n)
+
p=0
k:=1, N
xk
конец
При реализации алгоритмов, в программе обязательно нужно предусмотреть команды, которые меняют начальную базу генераций случайных чисел.
 2015-07-04
2015-07-04 1672
1672








