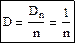
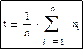 Смысл оценки заключается в следующем: пусть распределение случайной величины x определено, то есть известно значение некоторого параметра Θ. Нужно на основании выборочных значений x1, x2, …, xn, полученных при проведении n независимых испытаний, получить некоторую статистику t, которую с определенной степенью уверенности можно было бы принять за значение параметра Θ. В силу тех или иных причин (разного объема выборки, разных условий проведений опыта и другое) статистика t является случайной величиной, а значит нужно знать закон ее распределения или, по крайней мере, среднее значение и дисперсию. Тогда можно с определенной надежностью и точностью оценить неизвестное значение Θ. Пусть Θ – среднее значение x с σ2=1, тогда:
Смысл оценки заключается в следующем: пусть распределение случайной величины x определено, то есть известно значение некоторого параметра Θ. Нужно на основании выборочных значений x1, x2, …, xn, полученных при проведении n независимых испытаний, получить некоторую статистику t, которую с определенной степенью уверенности можно было бы принять за значение параметра Θ. В силу тех или иных причин (разного объема выборки, разных условий проведений опыта и другое) статистика t является случайной величиной, а значит нужно знать закон ее распределения или, по крайней мере, среднее значение и дисперсию. Тогда можно с определенной надежностью и точностью оценить неизвестное значение Θ. Пусть Θ – среднее значение x с σ2=1, тогда:
, то есть среднее значение t=Θ..
t имеет приближенно нормальное распределение:
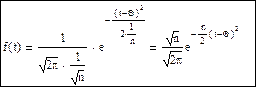
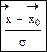
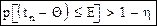 Эта формула показывает, что с возрастанием n, f(t) убывает, то есть говорят о том, что надежность оценки параметра Θ статистикой t возрастает вместе с числом опытов. Такой надежностью обладают так называемые состоятельные оценки. Оценка tn, вычисленная по выборке объемом будет состоятельной оценкой параметра Θ, если имеется число N, такое, что при всех n>N будет выполняться условие:, где Ε и η сколь угодно малые наперед заданные числа. То есть статистика tn будет состоятельной оценкой параметра Θ, если при n→∞, tn→∞. Пусть среднее значение выборки будет состоятельной оценкой
Эта формула показывает, что с возрастанием n, f(t) убывает, то есть говорят о том, что надежность оценки параметра Θ статистикой t возрастает вместе с числом опытов. Такой надежностью обладают так называемые состоятельные оценки. Оценка tn, вычисленная по выборке объемом будет состоятельной оценкой параметра Θ, если имеется число N, такое, что при всех n>N будет выполняться условие:, где Ε и η сколь угодно малые наперед заданные числа. То есть статистика tn будет состоятельной оценкой параметра Θ, если при n→∞, tn→∞. Пусть среднее значение выборки будет состоятельной оценкой 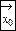 генеральной совокупности:
генеральной совокупности:
|
|
|
.
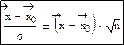 Для нормальной генеральной совокупности:
Для нормальной генеральной совокупности:
будет распределена со средним значением равным 0 и Dx=1, тогда:
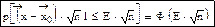 . Так как правая часть – это вероятность, то можно
. Так как правая часть – это вероятность, то можно
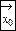
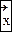
считать, что является состоятельной оценкой.
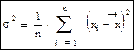 Аналогично можно доказать, что выборочная дисперсия:
Аналогично можно доказать, что выборочная дисперсия:
является состоятельной оценкой генеральной совокупности σ02. Свойство состоятельности оценки не требует никакого предположения о поведении статистики tn для конечного значения n.
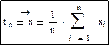 Пусть при всех n математическое ожидание tn равно Θ, каким бы ни был этот параметр. Тогда статистика tn называется несмещенной оценкой параметра Θ. Или оценкой без постоянной систематической погрешности. Для среднего значения выборки:
Пусть при всех n математическое ожидание tn равно Θ, каким бы ни был этот параметр. Тогда статистика tn называется несмещенной оценкой параметра Θ. Или оценкой без постоянной систематической погрешности. Для среднего значения выборки:
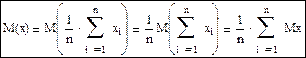
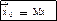 при среднем значении генеральной совокупности можно по теореме сложений математических ожиданий записать формулу:
при среднем значении генеральной совокупности можно по теореме сложений математических ожиданий записать формулу:
. Таким образом, математическое ожидание является не только состоятельной оценкой среднего значения генеральной совокупности, но и его несмещенной оценкой. Оценка дисперсии называется смещенной, так как существует формула. 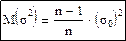
то есть статистика σ2 в среднем дает недооценку параметра σ02. Причем смещение равно: 
|
|
|
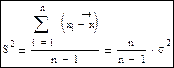 . Чтобы получить несмещенную оценку нужно взять следующую статистику:
. Чтобы получить несмещенную оценку нужно взять следующую статистику:
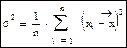 . Тогда M(S2)=σ02. S2 – это случайная величина, которая в среднем приближается к дисперсии генеральной совокупности. Условно выделяются две формулы: 1) Если нужно найти меру рассеяния выборки, то выбирается формула:
. Тогда M(S2)=σ02. S2 – это случайная величина, которая в среднем приближается к дисперсии генеральной совокупности. Условно выделяются две формулы: 1) Если нужно найти меру рассеяния выборки, то выбирается формула:
. 2) Если нужно найти оценку дисперсий генеральной совокупности, то нужно применить формулу вида: 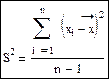
 2015-07-04
2015-07-04 685
685







