Прямые и обратные волны в длинной линии

Используя (1.8) - (1.11), а также связь u (x,t) и i (x,t) с комплексными амплитудами, перейдем к мгновенным значениям u (x,t) и i (x,t):

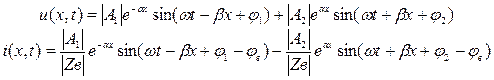(1.12)

где φ ₁ и φ ₂ аргументы комплексных величин А ₁ и А ₂, а φ_в – аргумент волнового сопротивления.

Как явствует из (1.12), каждое из решений представляет собой сумму двух слагаемых. Рассмотрим сначала первые из них:

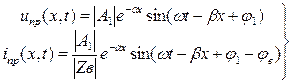(1.13)

Анализ (1.13) показывает, что они могут быть интерпретированы как бегущие волны соответственно напряжения и тока, распространяющиеся вдоль положительного направления оси х с коэффициентом затухания α. Эти бегущие волны получили название прямых (или падающих) волн напряжения и тока.

Определим длину волны этих волн λв. Так как по определению длина волны есть расстояние между двумя точками волны, взятыми в направлении её распространения, фазы в которых различаются на 2π, то

.

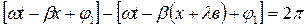Отсюда

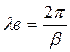(1.14)

Найдем скорость, с которой распространяется в линии прямая (падающая) волна. При этом под скоростью распространения в данном случае надо понимать скорость, с которой распространяется в линии состояние равной фазы волны, например, скорость, с которой перемещается вдоль линии некоторый нуль напряжения или тока.

Это условие можно выразить как:

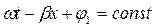
Откуда

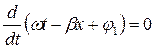
и, следовательно:

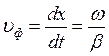(1.15)

Найденное выражение определяет так называемую фазовую скорость волны.

Если теперь обратиться ко вторым слагаемым решения (1.12),

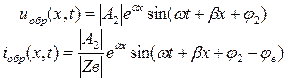(1.16)

то легко убедиться, что они описывают волну такого же характера, как и прямая, но распространяющуюся в обратном направлении. Эти волны получили название обратных (или отраженных) волн напряжения и тока.

Фазовая скорость обратной волны совпадает с точностью до знака с таковой для волны прямой. Амплитуда обратной волны напряжения или тока убывает в направлении от конца линии к ее началу.

Учитывая (1.13) и (1.16), выражения (1.8) и (1.9) можно представить в следующем виде:

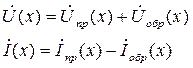(1.17)

где 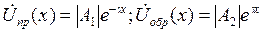- имеют смысл комплексных амплитуд прямой и обратной волн напряжения, а 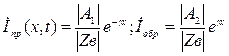- комплексных амплитуд падающей и отраженной волн тока.

Важно отметить, что для любой координаты х, т.е. для любой точки линии выполняется

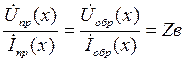(1.18)

Выражение (1.18) можно интерпретировать как закон Ома для прямых и обратных волн. Кроме этого (1.18) может быть использовано для определения физического смысла волнового сопротивления.

Введем понятие коэффициента отражения, которое играет важную роль в анализе цепей с распределенными параметрами. По определению коэффициент отражения в любом сечении линии х есть отношение комплексных амплитуд напряжения или тока обратной и прямой волн в этом сечении, т.е.

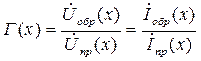(1.19)

Очевидно, Г(х) является комплексной величиной, причем |Г|≤ 1, если, разумеется, генератор подключен на входе в линию.

Постоянные интегрирования А ₁ и А ₂ могут быть найдены из граничных условий, т.е. по известным токам и напряжениям на входе или выходе длинной линии (рис. 2)

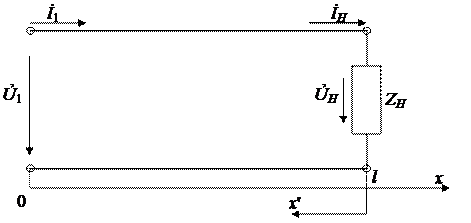
Рис. 2

Так, если при х =0 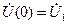; İ (0)= İ ₁, то согласно (1.17) Ủ ₁= А ₁+ А ₂, Zвİ ₁= А ₁+ А ₂.

Тогда:

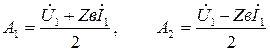(1.20)

Подставляя (1.20) в (1.19) дает выражение для коэффициента отражения в начале линии:

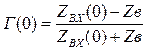(1.21)

где 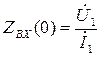входное сопротивление длинной линии.

Нетрудно обобщить формулу (1.21) на любое сечение длинной линии:

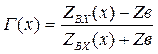(1.22)

где 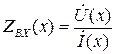- входное сопротивление линии в точке х.

Подставляя значения А ₁ и А ₂ из (1.20) в уравнения (1.8), (1.9), учитывая (1.21) и (1.22), получим:

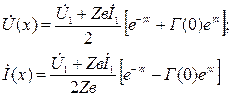(1.23)

Если граничные условия задаются в конце линии в месте подключения нагрузки при х=l, т.е. Ủ (l)= Ủ_Н, İ (l)= İ_Н, то

.

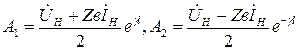Подставляя эти выражения в (1.8), получим:

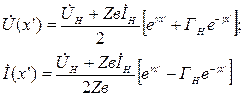(1.24)

Здесь 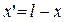– координата, отсчитываемая от конца линии (нагрузки), а Г_Н≡Г(l) и в соответствии с (1.22):

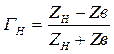(1.25)

Выражения (1.23) и (1.24) можно переписать и в другой форме. Учитывая формулы для А ₁ и А ₂, а также (1.17), получим для (1.23)

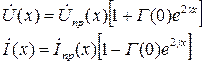(1.26)

аналогично для (1.24):

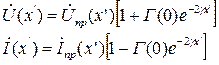(1.27)