Введение

Для специалиста в области транспортных машин при разработке автоматических устройств важное значение имеет понимание методов анализа и синтеза автоматических систем.

Переходный режим работы автоматических устройств автомобилей и тракторов является типичным режимом работы, поэтому анализ динамических характеристик и построение систем с заданными динамическими свойствами является одной из основных задач создания таких автоматических систем.

Анализ и оценка переходного процесса автоматической системы основаны на математическом описании каждого функционально-значимого элемента и системы в целом. Обычно свойства элементов не изменяются с течением времени и описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами. Это дает возможность применять известные в математике методы решения систем дифференциальных уравнений с постоянными коэффициентами. Однако стремление формализовать методы анализа и синтеза динамических систем предопределило использование специальных разделов математики (операционное исчисление и т. п.) и аппарата передаточных функций для описания физических процессов в системах автоматического регулирования.

В настоящем учебном пособии изложены математические основы теории автоматического регулирования: вводится понятие переходного процесса и его показателей качества, понятие об устойчивости; дается математическое описание динамических звеньев (передаточная функция, временные и частотные характеристики) и их связи с протекающими физическими процессами: приводятся методика математического описания автоматической системы в целом (понятие структурной схемы и правила формального преобразования, передаточная функция системы) и методом анализа устойчивости (критерии устойчивости и т. п.).

Материал пособия определен особенностями задач, решаемых при проектировании автоматических систем автомобилей и тракторов, их математическом описании и исследовании. Рассмотрены физические модели и приведены методы математического описания конкретных систем автоматического регулирования, динамические свойства которых непосредственно определяют эксплуатационные качества автомобилей.

1.ЭЛЕМЕНТЫ И ЗВЕНЬЯ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

1.1 Понятие динамического звена

Любая автоматическая система функционально состоит из нескольких взаимодействующих между собой физических элементов. Разбиение системы на функциональные элементы полезно при рассмотрении принципа действия автоматической системы.

Для качественного исследования и математического описания процессов автоматического управление расчленение автоматической системы на элементы часто не приносит пользы, так как управления многих элементов автоматически достаточно громоздки и различные элементы часто описываются однотипными уравнениями. При математическом описании автоматической системы удобно разбивать их не на элементы, а на динамические звенья. Под динамическим звеном понимается часть автоматической системы, описываемая дифференциальным уравнением определенного вида. Динамическим звеном может быть элемент системы, часть его, несколько элементов, рабочие процессы и даже вся система в целом. В любой автоматической системе может быть несколько динамических звеньев. Элементы различные по физической природе, конструкции, мощности и другим характеристикам, но описываемые уравнением одного и того же вида, являются одинаковыми динамическими звеньями.

Состояние динамического звена характеризуется совокупностью обобщенных координат на входе X и на выходе звена Y. В общем случае кроме входной величины на выходную величину звена могут оказать влияние и некоторые другие факторы, например, возмущающие воздействия Z. Переменные Y, X, Z обычно связаны между собой дифференциальными, интегральными и разностными уравнениями, содержащие время t в качестве независимой переменной. Тогда в общем виде выходная величина Y= f (X, Z), где f - вид математической зависимости.

Входные и выходные величины в зависимости от физической природы звена могут использовать различные переменные и их производные. Для механических звеньев это перемещение, скорость, ускорение, для пневматических – давление и расход воздуха, для электрических – ток, напряжение и их производные.

Динамическое звено обладает свойством однонаправленного действия, то есть оно передает взаимодействие только в направлении от входа к выходу и изменение выходной величины не влияет на входную.

1.2 Характеристики звеньев

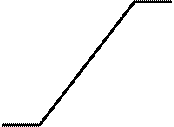
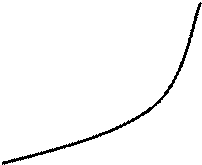
Зависимость выходной величины звена от входной в установившемся режиме называется статической характеристикой. По этой характеристике для каждого значения входной величины X можно определить соответствующее установившееся значение выходной координаты Y. Уравнение статической характеристики в общем виде Y= f (X). Характеристики могут быть (рис. 1.1а): линейными 1, нелинейными 2, с запаздыванием 3, с петлей гистерезиса 4. Линейная статическая характеристика может быть выражена уравнением Y = a + k X, где, а – постоянная величина, k – константа, характеризующая угол наклона прямой к оси абсцисс, которая называется статическим коэффициентом передачи или усиления.

Обычно статические характеристики элементов и звеньев автоматики кусочно-линейны или нелинейны. Линейные статические характеристики встречаются редко.

На рис. 1. 1б показаны три нелинейные характеристики элементов, у которых выходная величина определяется следующим образом:

характеристика 1 характеристика 2 характеристика 3

(с зоной нечувстви- (с насыщением) (идеальный

тельности) релейный)

K(a-X), при X <-a, -B, при X < -B/K, -A, при X<0

Y= 0,при |X|<a, Y= KX, при |X|<B/K, Y=
K(X-a), при X > a; B, при X > B/K; A, при X>0

Для элемента с зоной нечувствительности выходной параметр не реагирует на входной сигнал, величина которого меньше определенных значений (-а и а). Для элемента с насыщением изменение входного сигнала приводит к пропорциональному изменению выходного параметра до некоторой величины (-В и В), после чего наступает насыщение. Для идеального релейного элемента при изменении знака входного сигнала происходит мгновенное изменение выходного параметра.

Нелинейная статическая характеристика может рассматриваться как характеристика с переменным коэффициентом передачи К. В инженерной практике нелинейные характеристики приближенно заменяются линейными на основании разложения нелинейной функции в ряд Тейлора с последующим отбрасыванием нелинейных членов разложения.

Y Y

3

2

2 d A

b

1

1 X

A b d

0 x 3

Рис. 1. 1. Статистические характеристики систем

Следует иметь в виду, что статические характеристики некоторых элементов не поддаются линеаризации и они называются существенно нелинейными. Это характеристики релейных элементов типа '' да - нет'' с зоной нечувствительности (см. характеристику 3 на рис. 1. 1б).

Самопроизвольное изменение выходного параметра при неизменном входном определяет статическую погрешность характеристики. Различают абсолютную и относительную статические погрешности, которые дают полное представление о нестабильности статической характеристики.

Обычно автоматическая система работает в неустановившихся режимах. Поэтому важной задачей является изучение поведения систем именно в указанных режимах. В этом случае характеристика представляет собой изменение выходного параметра при изменении входного параметра и возмущающего воздействия его во времени, те есть когда X (t), Y (t) и Z (t) не остаются постоянными во времени. Такой режим является динамическим (неустановившимся), а характеристика называется переходной. Указанный режим работы является основным для автоматической системы.

1. 3. Переходный процесс и его оценочные показатели

Автоматическая система может работать как в установившемся (равновесном) режиме, так и в неустановившемся (неравновесном) режиме. В первом случае регулируемый параметр остается постоянным во времени, а во втором случае – меняется во времени. Неустановившийся ражим можно рассматривать как процесс перехода из первоначального равновесного состояния в другое равновесное состояние (или же возвращение к прежнему) в течение некоторого времени в результате воздействия входных и возмущающих факторов. Поэтому процесс неустановившегося режима работы называется переходным процессом.

Характер переходного процесса определяется видом входного и возмущающего воздействий, а так же динамическими свойствами звена и системы звеньев. Входные воздействия могут быть (рис. 1. 2): линейными 1, нелинейными 2, синусоидальными 3, периодическими 4, случайными 5.

X

5 1 2

6

4 3

0 t

Рис. 1. 2. Виды входных воздействий

Для оценки поведения автоматических систем и сравнения между собой различных автоматических систем применяются входные воздействия. Наиболее часто используются единичное ступенчатое и гармоническое (синусоидальное) воздействия, которые предназначены, прежде всего, для определения статической и динамической погрешностей работы автоматической системы.

Единичное воздействие характеризуется мгновенным (скачкообразным) изменением параметра от нуля до некоторой условной единицы (кривая 6 на рис. 1. 2).

Математическая запись ступенчатой функции имеет вид:

0, при t < 0

X (t) =

1, при t > 0

Такое единичное мгновенное ступенчатое воздействие характеризуется тем, что в момент времени t = 0 происходит скачкообразное изменение входной величины, которое остается постоянным при t > 0.

Математическая запись гармонического воздействия имеет вид:

X (t) = A Sin (wt)

где А и w – амплитуда и круговая частота воздействия.

Реакция автоматической системы или динамического звена при нулевых начальных условиях на входное воздействие в виде единичной ступенчатой функции времени (уравнения 1. 1) называется переходной характеристикой (переходной функцией) или временной характеристикой. Графическая интерпретация временной характеристики называется графиком переходного процесса. Вид временной характеристики определяется решением уравнения, описывающего автоматическую систему или звено, и характеризует динамические свойства объекта.

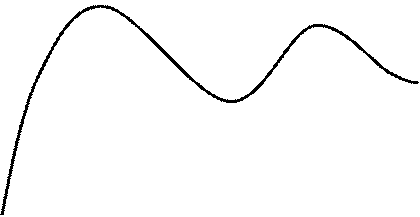
На рис. 1.3. приведены два характерных графика переходных процессов. Штрих-пунктирная линия определяет LimY(t) при t и определяет значение Y(). Заштрихованная область характеризует предельно-допустимую погрешность +, которая обычно выражается в процентах от Y ().

Основные показатели качества переходного процесса:

1. Время переходного процесса (регулирования) – Тр. Это время оценивает длительность переходного процесса и ограничивается тем моментом времени, когда кривая переходного процесса входит в область [Y () -, Y() + ] и в дальнейшем при изменении времени не выходит из этой области.

2. Перерегулирование б = [ Ymax – Y ()] / Y (), где Ymax – максимальное отклонение выходного параметра. Обычно, допустимое Перерегулирование принимается не более (10…30) %. Перерегулирование может и отсутствовать, когда процесс монотонный (кривая 1. на графике).

3. Число колебаний кривой переходного процесса за время переходного процесса.

y 1 2

y max б

Y ()

Tp t

Рис. 1. 3. Характерные графики переходных процессов

1 – Монотонный процесс, 2 – Колебательный процесс

2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПИСАНИЯ ДИНАМИЧЕСКИХ ПРОЦЕССОВ

2.1 Описание переходного процесса

При математическом описании переходного процесса обычно используются дифференциальные уравнения. Эти уравнения составляются на основании физических знаков:

а) Для механических систем – законов Ньютона;

в) Для гидропневматических систем – законов течения жидкости и воздуха;

с) Для электрических систем – законов Кирхгофа и т.д.

В системе находится чувствительный элемент и рассматривается условие его равновесия. Условия равновесия для механических систем формулируется на основе принципа Даламбера–Лагранжа. По этому принципу для механической системы с идеальными удерживающими связями сумма элементарных работ всех сил, приложенных к системе, на любом возможном перемещении в каждый данный момент равна 0.

Тогда уравнения составляются в следующей последовательности:

1. Устанавливается входные и выходные параметры.

2. Определяется чувствительный элемент, который воспринимает различные силы.

3. Составляется уравнение равновесного состояния чувствительного элемента. Для механической системы левая часть уравнения обычно состоит из следующих слагаемых:

а) m (d^2 y / dt^2) – сила инерции движущихся масс m, приведенных к чувствительному элементу;

в) v (dy / dt) – сила вязкого трения (v – коэффициент трения);

с) с y – силы упругости (с – коэффициент жесткости) и т.п.

В правой части уравнения пишутся внешние силы F (x), действующие на чувствительный элемент. Таким образом, в левой части уравнения записываются выражения, содержащие выходную величину и ее производные, а в правой части – выражения, содержащие входную величину. Обычно рассматриваются элементы, свойства которых не изменяются с течением времени и каждый динамический процесс зависит лишь от начального состояния элемента (от начальных условий) и характера внешних воздействий.

При составлении уравнений необходимо знание всех параметров, влияющих на работу каждого звена. В этом случае составленное уравнение будет близко отображать действительные процессы. Конечно, в этом случае полученные уравнения могут оказаться сложными, что затруднит их решение. Для практических целей, возможно, исключать некоторые параметры и звенья, упрощать взаимосвязи звеньев.

Общий вид дифференциального уравнения для механической системы n – порядка будет иметь следующий вид:

A0 Yⁿ + A1 Y^(n-1) + An-1 Y + An = f (t) (2. 1)

Где Y^n производная n-го порядка по времени от выходного сигнала,

А0, А1…Ап – постоянные коэффициенты,

f (t) – функция, определяющая закон изменения во времени входного сигнала X (t) (считается известной).

Если дифференциальное уравнение (2. 1) не линейное, то оно заменяется приближенным линейным, то есть нелинейное дифференциальное уравнение подвергают линеаризации. Аналитически линеаризация производится с помощью разложения в ряд Тейлора функции в окрестности точки, соответствующей установившемуся состоянию, и отбрасыванием всех членов, содержащих отклонение выходной величины элемента в степени высшей первой. При линеаризации в левой части уравнения составляют лишь члены, содержащие отклонения выходной величины, а все остальные члены переносятся в правую часть.

Например, для безинерционного нелинейного звена с законом преобразования входного сигнала Х в выходной Y = f (x) линеаризованная связь между ними имеет вид:

Y = f (X0) + df / dx (X – X0), (2. 2)

где X0 – установившееся значение параметра Х.

2.2 Преобразование Лапласа

Для решения линейных дифференциальных уравнений, описывающих поведение систем автоматики, применима операционное исчисление. При операционном исчислении используются такие методы математического аппарата, которые позволяют простыми и экономичными средствами получать решения линейных дифференциальных, интегральных и разностных уравнений. Наибольшее применение нашло преобразование Лапласа. Его идея состоит в переходе от функций, зависящих от времени t, к их изображениям – функциям, зависящим от комплексной переменной s, то есть функция – оригинал X (t) переводится в функцию-изображение X (s). Таким образом, с помощью преобразования Лапласа функция действительного переменного заменяется функцией комплексной переменной. Связь между функцией X (t) и ее лапласовым изображением X (s) при X > 0 будет иметь следующий вид:

a) При преобразовании функции X (t) в ее изображение X (s)

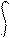
L [ X (t) ] = X (s) = X (t) e^(-st) dt; (2.3)

б) При преобразовании изображения X (s) в его функцию X (t)

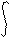
c+i

L [ X (s) ] = X (t) = 1 / 2П i X (s) e^st ds, (2.4)

c-i

где e^st – комплексная функция действительного переменного t.

s = a + i b, где a > 0 действительная, b – мнимая части комплексной переменной, i^2 = -1.

Таким образом, при преобразовании Лапласа:

1) Некоторая функция – оригинал X (t) вещественной переменной t преобразуется в другую функцию – изображение X (s) комплексного переменного s.

X (t) X (s). (2.5)

2) Производная функции X (t) n – порядка преобразуется в алгебраическое произведение комплексной переменной s^n на изображение X (s) самой функции (при нулевых начальных условиях):

L (dX^n / dt^n) = s^n X (s) (2.6)

Это следует из:

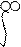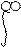L (dX / dt) = e^(-st) (dX / dt)dt = [ (d / dt) (e^(-st) X) – (d / dt)(e^(st))X ]dt=

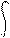
= e^(-st) X (t) + s e^(-st) X (t)dt = s X (s) – X (0).

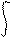3) Изображение интегральной функции f (t)dt сводится к алгебраическому делению изображения X (s) на комплексную переменную s (при нулевых начальных условиях):

L [ f (t)dt ] = X (s) / s (2.7)

4) Сумма оригиналов равна сумме изображений

L [X1(t) + X2(t) +…+Xn(t)] = X1(s) + X2(s) +…+ Xn(s). (2.8)

5) Коэффициенты членов уравнений в оригинале остаются без изменения в уравнениях с изображениями.

Операционное исчисление с использованием преобразования Лапласа нашло самое широкое применение в теории автоматических систем для расчета переходных процессов. Решение осуществляется в три этапа.

1-й этап. Переход от оригиналов к изображениям, то есть переход от дифференциального уравнения к алгебраическому уравнению.

2-й этап. Решение алгебраического уравнения.

3-й этап. Переход от полученного уравнения в изображениях к оригиналу.

В таблице 2.1. приведены некоторые оригиналы и их изображения при преобразовании по Лапласу [7].

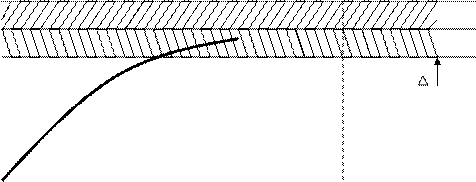
Составление линейного дифференциального уравнения второго порядка по переменной t и его преобразования в линейное алгебраическое уравнение по комплексной переменной s покажем на примере золотникового гидрораспределителя (рис. 2.1.). Такого типа гидрораспределители широко применяются в автоматических системах. Они обладают малым трением и уравновешены от статических сил давления. Показанный гидрораспределитель предназначен для преобразования усилия на штоке 3 в механическое перемещение подвижных частей, а затем в движение потока жидкости, поступающей в исполнительные элементы. Следовательно, входной величиной является сила Х, действующая на шток золотника, а выходной величиной является смещение золотника Y.

Золотник 1 удерживается в корпусе 2 при помощи двух пружин 4 в нейтральном положении. Под действием силы Х золотник перемещается вдоль оси от своего нейтрального положения на величину Y. При этом на золотник действует еще сила трения Fтр и сила упругой деформации пружины Fпр. Тогда уравнение золотника будет иметь вид:

m (d^2 Y / dt^2) + Fтр + Fпр = X, (2.9)

где m – масса золотника и других подвижных частей.

Таблица 2.1

Прямые преобразования Лапласа

Изображение	Оригинал	Изображение	Оригинал
1 / s		n! / s^(n+1)	t^n
a / (s^2+a^2)	Sin (at)	2sa (s^2+a^2)^2	T Sin (at)
s / (s^2+a^2)	Cos (at)	1/s^2(s+a)	(e^(-at)+at-1)/a^2
1 / (s^2+a^2)	e^(at)	1/(s+a)^2	t e^(at)
a/[(s+a)^2+a^2]	e^(-at)Sin (at)	(s^2-a^2) (s^2+a^2)^2	T Cos (at)
(s + a) [(s+a)^2+a^2]	e^(-at)Cos(at)	1/(s^2+a^2)^2	Sin(at)-atCos(at) 2 a^3

Сила трения Fтр при жидком трении пропорциональна скорости перемещения dX / dt. Коэффициент пропорциональности для таких золотников можно считать постоянной величиной, так как подвижные части изготовлены с высокой точностью, а смещения их достаточно малы. Тогда Fтр= v (dY/dt). Когда золотник под действием сил смещается, то он преодолевает и силы упругости пружин. Сопротивление пружин пропорционально перемещению и определяется как Fпр= cY, где с – коэффициент жесткости пружины.

Теперь, имея уравнение для всех сил, напишем общее дифференциальное уравнение золотникового распределителя

m (d^2Y)/dt^2 + v (dY/dt) + c Y.

Как видно, уравнение является линейным.

Далее, разделим все члены уравнения на с. После этого получим уравнение с коэффициентами в виде постоянных времени:

T2^2(d^2Y/dt^2) + (T1(dY/dt) + Y = K X.

Используя преобразование Лапласа, это уравнение можно записать в следующей операторной форме

(T2^2s^2 + T1s + 1) Y = K X, (2.10)

где T2^2 – постоянная времени и характеризует инерционность подвижных частей Т2^2 = m/c = 1/w, где w – частота колебаний; Т1 –постоянная времени и характеризует демпфирующие свойства распределителя Т = n/с; К – коэффициент усиления распределителя К = 1/с.

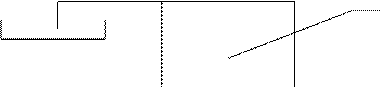
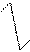
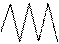
3

Fпр Fтр X

Y

2 1 6

Рис. 2.1. Золотниковый гидрораспределитель

1-золотник, 2- корпус, 3- шток золотника, 4- пружины, 5- подвод жидкости от насоса, 6- отвод жидкости к исполнительным элементам

Перемещение Y является выходным сигналом, а сила Х – входным. Тогда уравнение (2.10) является частным случаем общего уравнения:

Dy (s) Y(s) = K Dx (s) X(s), (2.11)

где Dy(s) – оператор выхода или собственный оператор,

Dx(s) – оператор входа.

В рассмотренном выше примере Dx(s) = 1, Dy(s) = 1 + T1s + T2^2 S^2.

Название «собственный» оператор Dy(s) обусловлен тем, что многочлен характеризует собственное движение элемента, то есть его движение при отсутствии внешних возмущающих и управляющих воздействий.

В равновесном (статистическом) состоянии s = 0 и тогда получим вырожденный вариант уравнения: Y = K X.

При воздействии на систему и управляющего X(s) и возмущающего Z(s) сигналов операторное дифференциальное уравнение и в общем виде запишется так:

Dy(s) Y(s) = K Dx(s) X(s) + Dz(s) Z(s).

К линейной автоматической системе применим принцип суперпозиции. Если к системе приложено несколько воздействий, то суммарный эффект от этих воздействий может быть определен как сумма эффектов от каждого из воздействий. Тогда частное решение дифференциального уравнения есть сумма частных решений от каждого воздействия. При определении частного решения от одного воздействия остальные воздействия можно считать равными 0. Для нелинейных уравнений этот принцип не применим.

2.3 Понятие передаточной функции

Из уравнения (2.11) в общем виде можно записать следующее отношение:

W(s) = Y(s) / X(s) = K Dx(s) / Dy(s). (2.12)

Это отношение при нулевых начальных условиях называется операторной передаточной функцией. Из уравнения (2.12) следует два определения передаточной функции:

1. Передаточная функция – это отношение операторного изображения Y(s) выходной величины к операторному изображению X(s) входной величины.

2. Передаточная функция – это отношение входного оператора Dx(s) к собственному оператору Dy(s), умноженое на статистический коэффи

циент передачи.

Передаточную функцию также называют динамическим коэффициентом передачи, по аналогии со статистикой, так как при s = 0 W(s) = K.

Передаточная функция является важнейшей характеристикой динамического звена. Каждое динамическое звено можно описать передаточной функцией, которая полностью характеризует его собственное движение и динамические свойства. Таким образом передаточная функция является основным параметром, определяющим вид динамического звена. Это значительно упрощает анализ систем, так как задача составления дифференциальных уравнений системы в целом сводится к составлению дифференциальных уравнений отдельных динамических звеньев.

Зная передаточную функцию и изображение входного воздействия X(s), при заданных начальных условиях всегда можно определить изображение Y(s) выходного параметра:

Y(s) = W(s) X(s).

Как видно из выше изложенного, динамическое звено - это математическая модель элемента (или части сложного элемента), который отображает лишь его динамические свойства, а не физическую сущность происходящих в нем процессов. Математическая модель выражается передаточной функцией. Динамические звенья различаются по виду переходного процесса, получаемого на основе решения математической модели.

2.4 Типовые динамические звенья

По своим основным свойствам динамические звенья можно разделить на три группы типовых звеньев: позиционные, интегрирующие и дифференцирующие.

Позиционные: усилительные (безинерционное) звено, апериодическое (инерционное) звено первого порядка, колебательное звено, апериодическое (инерционное) звено второго порядка и консервативное звено. Позиционные звенья характеризуются тем, что с течением времени устанавливается постоянное значение входного параметра при постоянном значении входного параметра.

Усилительное звено характеризуется тем, что выходной параметр в любой момент времени воспроизводит входной, измененный в К раз без запаздывания и сдвига по фазе. Переходный процесс в усилительном звене отсутствует.

Апериодическое (первого порядка) – выходной параметр изменяется монотонно, достигая некоторого установившегося значения. Это звено так же называется статическим, одноемкостным, инерционным, релаксационным.

Колебательное - в этом звене связь между входным и выходным параметрами выражается уравнением второго порядка и переходный процесс имеет колебательный характер.

Апериодическое (второго порядка) и консервативное – это варианты колебательного звена и описываются теми же уравнениями.

Интегрирующие звенья (интегрирующее идеальное, интегрирующее инерционное и изодромное) характеризуется тем, что выходной параметр неограниченно возрастает при постоянном значении входного параметра: интегрирующее идеальное – выходной параметр пропорционален интегралу по времени от входного параметра; интегрирующее инерционное – представляет собой совокупность двух последовательно включенных звеньев: идеального интегрирующего и апериодического первого порядка; изодромное – совокупность двух параллельно соединенных звеньев: идеального интегрирующего и усилительного.

Дифференцирующие звенья (идеальное и реальное) характеризуются тем, что выходной параметр реагирует лишь на изменение входного параметра: идеальное – выходной параметр пропорционален скорости изменения входного параметра; реальное – выходной параметр мгновенно возрастает до значения пропорционального коэффициенту усиления, как у идеального звена, а затем убывает по экспоненте.

2.5 Характеристики тепловых динамических звеньев

При рассмотрении типовых динамических звеньев необходимо определять следующие параметры и характеристики:

1. Дифференциальное уравнение по переменной время t.

2. Уравнение переходного процесса (решение дифференциального уравнения).

3. Алгебраическое уравнение по переменной s.

4. Передаточная функция по переменной s.

5. Частотная передаточная функция.

6. Графики:

а) Переходного процесса (временная характеристика),

б) Амплитудно-фазовая характеристика (АФХ),

в) Амплитудно-частотная характеристика (АЧХ),

г) Фазо-частотная характеристика (ФЧХ),

д) Логарифмическая частотная характеристика (ЛЧХ).

Указанные характеристики приведены в табл. 2.2, 2.3, 2.4, 2.5.

Для апериодического звена уравнение переходного процесса получается при решении его дифференциального уравнения путем интегрирования при нулевых начальных условиях. Кривая переходного процесса представляет собой монотонную экспоненту, которая стремится к некоторому установившемуся значению Y (∞). Из графика переходного процесса следует:

а) передаточный коэффициент звена К = Y (∞) / X и Y (∞) K X.

б) постоянная времени Т определяет значение выходного параметра:

Y = K X(1-e^(-t/T)) – Y(∞)(1-1/e) = 0,63 Y(∞)

и может находиться графически путем проведения касательной к кривой в начале координат до пересечения прямой Y(∞). Проекция этой касательной на ось абсцисс и дает время Т.

в) время переходного процесса Тр = 3Т. Это время определяется графическим путем построения зоны статистической погрешности процесса. Вход кривой в эту зону и определяет время переходного процесса.

Для колебательного звена должно соблюдаться условие (Т1 – 2Т2) < 0. Иногда определяют отношение Т1 – 2Т2 = x - коэффициент демпформирования. Этот коэффициент должен находится в следующих пределах 0 < x <1

.

Уравнение переходного процесса так же получается при решении его дифференциального уравнения.

Для апериодического звена второго порядка коэффициент дифформирования x > 1 и соответственно Т1 > 2Т2. Переходной процесс уже не будет колебательным, а выражается апериодической кривой. Это звено может быть представлено как два последовательных апериодических (инерционных) звена.

На любое динамическое звено могут воздействовать гармонические сигналы постоянной амплитуды А, частоты W. Тогда после затухания переходного процесса на выходе установится тоже гармоническое изменение выходной величины с той же частотой, но с другой амплитудой В и с отставанием по фазе на угол φ. Тогда можно записать X(t) = A Sin(wt) и Y = B Sin(wt+φ). Обычно уравнения записываются в показательной форме: X(t) = A e^(iwt) и Y(t) = = B e^(i (wt+φ). На основе последних уравнений получим следующее отношение:

Y(t) B e^(i (wt+φ)) B

= = e^iφ = W(iw). (2.13)

X(t) A e^(iwt) A

Это отношение представляет собой частотную передаточную функцию. Частотная передаточная функция может быть получена из операторной функции подстановкой s = iw.

Используя выражение частотной передаточной функции можно получить следующие частотные характеристики:

1. Амплитудно-фазовая частотная характеристика. Используя формулу Эйлера, напишем е^iφ = Cos φ(w) + i Sin φ(w). Тогда частотная передаточная функция запишется в следующем виде:

B

W (iw) = (w) [Cos φ(w) + Sin φ(w) ].

A

Как видно, частотная передаточная функция представляет собой функцию комплексного переменного, состоящую из вещественной части и мнимой частей:

W(iw) = ReW(iw) + JmW(iw). (2.14)

Таким образом, амплитудно-фазовая частотная характеристика представляет собой геометрическое место концов векторов, длины которых при изменении w от 0 до ∞ равны отношению амплитуд В/А(w), а углы по отношению к вещественной оси равны φ(w). Значения ReW(iw) и JmW(iw) представляет собой проекции векторов на вещественную и мнимую оси плоскости комплексного переменного.

2. Амплитудно-частотная характеристика представляет собой модуль W(iw). Это следует из общего определения комплексной величины:

|W(iw)| = √[ ReW(iw) ]^2 + [ JmW(iw) ]^2. (2.15)

3. Фазо-частотная характеристика также вытекает из общего определения комплексной величины:

φ = arctg [ JmW(iw) / ReW(iw) ]. (2.16)

4. Логарифмическая частотная характеристика представляет собой зависимость логарифмической амплитудной частотной функции L(w) от логарифма частоты L(w):

L(w) = 20 L [W(iw) ]. (2.17)

Кривые переходного процесса и частотные характеристики можно определить экспериментально для любого физического элемента. Тогда по виду полученных кривых определяют типовое звено. Определение типового динамического звена по кривой переходного процесса. На вход элемента подается сигнал в виде единичной ступенчатой функции, а с выхода элемента снимают выходной сигнал на самопишущий прибор. По виду полученной кривой определяют тип звена.

При определении типа звена по частотным характеристикам на вход элемента подается гармоническое входное воздействие от специального генератора с постоянной амплитудой и фазой, а частота может плавно изменяться в широких пределах. На выходе по приборам регистрируют амплитуду и фазу. Изменяя частоту можно построить частотную характеристику, которую сравнивают с характеристикой типовых звеньев.