Имеется множество задач с параметром, в которых фигурирует уравнение или неравенство, сводящееся к квадратному заменой неизвестного. Здесь важно правильно переформулировать условие задачи для нового неизвестного. Часто новая задача состоит в исследовании знака корней квадратного уравнения.
5. При каких значениях 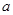 уравнение
уравнение 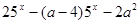
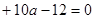 не имеет действительных корней? Решение. С помощью замены
не имеет действительных корней? Решение. С помощью замены 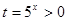 приводим данное уравнение к квадратному уравнению
приводим данное уравнение к квадратному уравнению 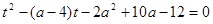 . Это квадратное уравнение не должно иметь положительных корней. Найдем его дискриминант
. Это квадратное уравнение не должно иметь положительных корней. Найдем его дискриминант 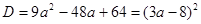 . Поскольку дискриминант является полным квадратом, то в данном случае корни получатся рационально зависящие от параметра. Есть смысл решить это уравнение и потребовать, чтобы корни были не положительны:
. Поскольку дискриминант является полным квадратом, то в данном случае корни получатся рационально зависящие от параметра. Есть смысл решить это уравнение и потребовать, чтобы корни были не положительны: 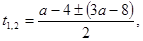
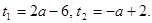 Отсюда
Отсюда 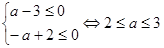 . Ответ:
. Ответ: 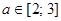 .
.
6. При каких значениях параметра 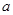 уравнение
уравнение 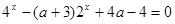 имеет единственный корень? Решение. Соответствующее квадратное уравнение
имеет единственный корень? Решение. Соответствующее квадратное уравнение 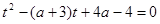 ,
, 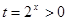 должно иметь единственный положительный корень. Найдем его дискриминант
должно иметь единственный положительный корень. Найдем его дискриминант 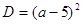 . Здесь также дискриминант является полным квадратом, есть смысл найти корни:
. Здесь также дискриминант является полным квадратом, есть смысл найти корни: 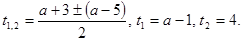 Значит, при любом значении
Значит, при любом значении 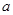 имеется положительный корень. Тогда второй корень либо должен быть неположительным, либо совпадать с первым. Отсюда либо
имеется положительный корень. Тогда второй корень либо должен быть неположительным, либо совпадать с первым. Отсюда либо 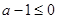 , либо
, либо 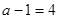 . Ответ:
. Ответ: 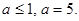
|
|
|
7. При каких значениях 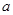 уравнение
уравнение 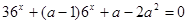 имеет два различных корня? Решение. Соответствующее квадратное уравнение должно иметь два различных положительных корня. Так как
имеет два различных корня? Решение. Соответствующее квадратное уравнение должно иметь два различных положительных корня. Так как 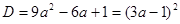 — полный квадрат, то в данном случае короче будет решить это уравнение:
— полный квадрат, то в данном случае короче будет решить это уравнение: 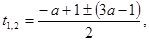
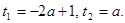 Отсюда получаем
Отсюда получаем 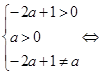
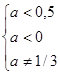 . Ответ:
. Ответ: 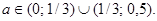
8. При каких значениях параметра 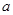 уравнение
уравнение 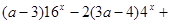
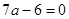 имеет единственное решение? Решение. С помощью замены
имеет единственное решение? Решение. С помощью замены 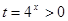 приводим данное уравнение к уравнению
приводим данное уравнение к уравнению 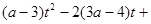
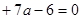 . Это уравнение должно иметь единственный положительный корень. Сначала рассмотрим случай, когда уравнение не является квадратным, т. е.
. Это уравнение должно иметь единственный положительный корень. Сначала рассмотрим случай, когда уравнение не является квадратным, т. е. 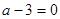 . В этом случае получаем уравнение
. В этом случае получаем уравнение 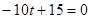 , имеющее положительный корень. Значит, данное значение
, имеющее положительный корень. Значит, данное значение 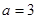 нужно включить в ответ. Теперь возьмем
нужно включить в ответ. Теперь возьмем 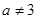 . Найдем его дискриминант
. Найдем его дискриминант 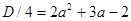 . Если
. Если 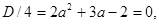
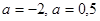 , то уравнение имеет единственный корень, но нужно проверить его знак. Корень уравнения при
, то уравнение имеет единственный корень, но нужно проверить его знак. Корень уравнения при 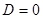 имеет вид
имеет вид 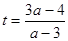 . Подставляя
. Подставляя 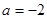 и
и 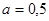 , убеждаемся, что и в том, и в другом случае корень положительный. Еще возможна ситуация, когда один корень положительный, а другой отрицательный, либо равный нулю. При каких значениях параметра корни имеют разные знаки? Это можно определить по теореме Виета: в приведенном уравнении свободный член должен быть отрицательным. Так как приведенное уравнение имеет вид
, убеждаемся, что и в том, и в другом случае корень положительный. Еще возможна ситуация, когда один корень положительный, а другой отрицательный, либо равный нулю. При каких значениях параметра корни имеют разные знаки? Это можно определить по теореме Виета: в приведенном уравнении свободный член должен быть отрицательным. Так как приведенное уравнение имеет вид 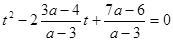 , то получаем условие
, то получаем условие 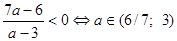 . Если один корень равен 0, то
. Если один корень равен 0, то 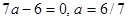 . Подставляем это значение в уравнение
. Подставляем это значение в уравнение 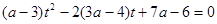 и получаем уравнение
и получаем уравнение 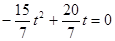 , у которого второй корень больше 0. Значит, это значение
, у которого второй корень больше 0. Значит, это значение 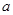 также нужно включить в ответ. Окончательно,
также нужно включить в ответ. Окончательно, 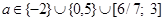 . Ответ:
. Ответ: 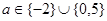
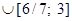 .
.
|
|
|
9. При каких значениях параметра 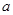 неравенство
неравенство 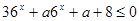 имеет решение? Решение. Соответствующее квадратное неравенство
имеет решение? Решение. Соответствующее квадратное неравенство 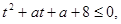
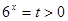 , должно иметь положительные решения. Это значит, что уравнение
, должно иметь положительные решения. Это значит, что уравнение 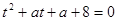 должно иметь хотя бы один положительный корень. В данном случае будет не очень сложно решить это уравнение и потребовать, чтобы его больший корень был положителен. Находим корни:
должно иметь хотя бы один положительный корень. В данном случае будет не очень сложно решить это уравнение и потребовать, чтобы его больший корень был положителен. Находим корни: 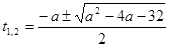 , очевидно, большим является корень
, очевидно, большим является корень 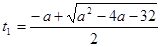 . Получаем неравенство
. Получаем неравенство 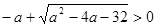
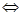
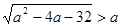 . Вспомним схему решения иррационального неравенства. Данное неравенство равносильно совокупности двух систем 1)
. Вспомним схему решения иррационального неравенства. Данное неравенство равносильно совокупности двух систем 1) 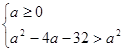 и 2)
и 2) 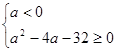 . Первая система решений не имеет, решение второй системы
. Первая система решений не имеет, решение второй системы 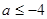 . Ответ:
. Ответ: 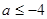 .
.
10. При каких значениях параметра 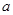 уравнение
уравнение 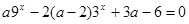 имеет хотя бы один корень? Решение. Проще разобраться, когда уравнение не имеет ни одного корня, или когда уравнение
имеет хотя бы один корень? Решение. Проще разобраться, когда уравнение не имеет ни одного корня, или когда уравнение 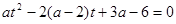 не имеет ни одного положительного корня. Для этого, во-первых, рассмотрим случай, когда корней нет вообще:
не имеет ни одного положительного корня. Для этого, во-первых, рассмотрим случай, когда корней нет вообще: 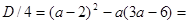
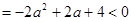
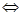
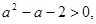

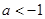 ,
, 
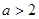 . Во-вторых, определим, когда все имеющиеся корни квадратного уравнения не положительны. При
. Во-вторых, определим, когда все имеющиеся корни квадратного уравнения не положительны. При 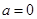 получаем
получаем 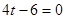 ,
, 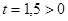 . При
. При 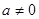 применим формулы Виета для корней приведенного уравнения, потребуем, чтобы сумма корней, равная
применим формулы Виета для корней приведенного уравнения, потребуем, чтобы сумма корней, равная 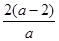 , была не положительна, а произведение, равное
, была не положительна, а произведение, равное 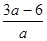 , не отрицательно. Рассмотрим систему
, не отрицательно. Рассмотрим систему 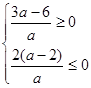
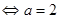 , утверждающую, что оба корня не положительны.. Мы получили, что квадратное уравнение не имеет положительных корней при
, утверждающую, что оба корня не положительны.. Мы получили, что квадратное уравнение не имеет положительных корней при 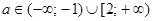 . Значит, при значениях параметра в промежутке
. Значит, при значениях параметра в промежутке 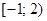 существует хотя бы один положительный корень. Ответ:
существует хотя бы один положительный корень. Ответ: 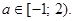
11. При каких значениях параметра 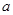 уравнение
уравнение 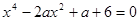 имеет решение? Решение. Обозначим
имеет решение? Решение. Обозначим 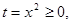
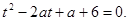 Это уравнение должно иметь хотя бы один неотрицательный корень. Проще решить уравнение и потребовать, чтобы его больший корень был неотрицательным:
Это уравнение должно иметь хотя бы один неотрицательный корень. Проще решить уравнение и потребовать, чтобы его больший корень был неотрицательным: 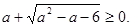 Кстати, повторим, как решать иррациональные неравенства: неравенство
Кстати, повторим, как решать иррациональные неравенства: неравенство 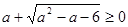
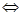
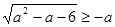 равносильно совокупности систем
равносильно совокупности систем 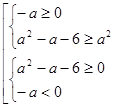 . Первая система совокупности имеет решение
. Первая система совокупности имеет решение 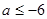 . Решаем вторую систему, входящую в совокупность:
. Решаем вторую систему, входящую в совокупность: 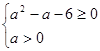
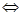
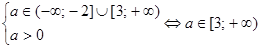 . Объединяя эти промежутки, получаем
. Объединяя эти промежутки, получаем 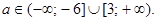 Ответ:
Ответ: 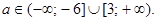
 2015-07-04
2015-07-04 2413
2413
