Использование бинарного дерева поиска для построения таблицы идентификаторов

Дерево является одной из самых распространенных структур, используемых для представления данных в памяти компьютера. Известно много разновидностей этой структуры и детально изучены свойства каждой из них [10]. Мы ограничимся рассмотрением бинарных деревьев поиска, использование которых для построения таблиц идентификаторов позволяет сократить время поиска элемента в таблице, не увеличивая значительно времени заполнения таблицы.

Деревом называется конечное множе­ство, состоящее из одного или более элементов, называемых узлами, таких, что:

1) между узлами имеет место отношение типа «исход­ный-порожденный»;

2) есть только один узел, не имеющий исходного, - он называется корнем;

3) все узлы, за исключением корня, имеют только один исходный;

4) каждый узел может иметь несколько порож­денных;

5) отношение «исходный-порожденный» действует только в одном направлении, то есть ни один потомок некоторого узла никогда не может стать для него предком.

Число порожденных узлов отдельного узла называется степенью данного узла. Максимальное значение степени всех узлов дерева называется степенью дерева.

Дерево, все узлы которого имеют степень не больше 2, называется бинарным деревом. Бинарное дерево представляет собой ко­нечное множество узлов, которое:

1) или пусто,

2) или состоит из одного корня и двух бинарных деревьев, называемых левым, и правым поддеревьями этого корня.

Из определения следует, что дерево, у которого корень имеет только левое поддерево, и дерево, у которого корень имеет только правое поддерево, считаются разными.

Если в дереве между порожденными узлами, имеющими об­щий исходный, считается су­щественным их порядок, то дерево называется упорядочен­ным. Очень важным является тот факт, что при поиске почти во всех случаях имеют дело с упорядоченными деревьями.

Бинарным деревом поиска называют такое бинарное дерево, в котором для каждого узла дерева все ключи в левом поддереве меньше, а в правом поддереве больше значения ключа данного узла.

Для того чтобы структуру произвольного бинарного дере­ва представить в памяти ЭВМ, необходимо как минимум сле­дующее:

1) каждый узел должен содержать один ключ и два ука­зателя на левое и правое поддеревья;

2) если узел не имеет левого и (или) правого поддеревьев, то указатель на соответствующее поддерево будет пустым (NULL);

3) чтобы сделать дерево доступным для обработки, необ­ходимо задать указатель на корень root.

Вышеописанную структуру следует рассматривать не более как схему. Например, в узле могут храниться кроме ключа также и данные, если они имеют небольшой объем. При большом объеме таких данных их хранят обычно от­дельно, а в узел включают соответствующий указатель. Ча­сто бывает целесообразно хранить в каждом узле не только указатели на порожденные поддеревья, но и указатель на исходный узел. Кроме того, для упрощения поиска жела­тельно иметь в каждом узле данные о числе узлов левого поддерева: (число узлов левого поддерева данного узла) + 1. Однако в связи с тем, что все эти расширения приводят не только к увеличению занимаемого пространства памяти, но и к усложнению операций обновления данных, необходимо очень тщательно анализировать все плюсы и минусы в зави­симости от того, какие данные хранятся в узле и в каком виде, какие операции будут выполняться над деревьями, ка­ковы объем памяти и вычислительные ресурсы компьютера, который будет использоваться.

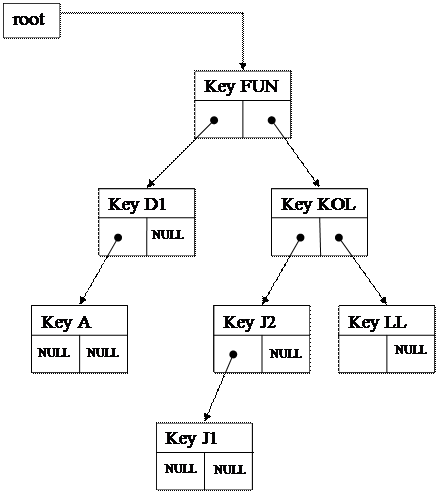
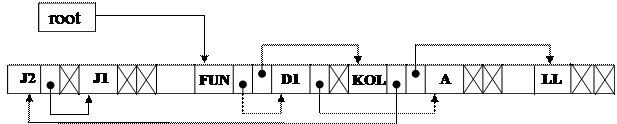
Пример струк­туры бинарного дерева поиска и его отображения на память компьютера показан на рис. 3.3. В нашем случае каждый узел бинарного дерева поиска представляет собой элемент таблицы идентификаторов, к которому для организации связи добавлены два дополнительных поля – указатели на правое и левое поддеревья. Таким образом, бинарное дерево поиска легко реализуется в виде нелинейного двусвязного списка.

Алгоритм заполнения таблицы идентификаторов по методу бинарного дерева поиска, достаточно прост. В ходе лексического разбора исходного текста программы порождается входной поток данных, содержащий идентификаторы. Первый идентификатор считается корнем дерева. Все последующие идентификаторы помещаются в дерево в соответствии с нижеприведенным алгоритмом.

Шаг 1. Выбрать очередной идентификатор из входного потока данных. Если такового нет, то построение дерева закончено.

Шаг 2. Сделать текущим узлом корень дерева.

Шаг 3. Сравнить очередной идентификатор с ключом текущего узла дерева. Если очередной идентификатор меньше текущего ключа, то перейти к шагу 4; если равен – сообщить об ошибке (двух одинаковых идентификаторов быть не должно) и прекратить выполнение алгоритма; иначе - перейти к шагу 6.

Шаг 4. Если у текущего узла существует левое поддерево, то сделать его корень текущим узлом и перейти к шагу 3; иначе – перейти к шагу 5.

Шаг 5. Создать новый узел; поместить в него очередной идентификатор как значение ключа; в указатель на левое поддерево текущего узла записать адрес вновь созданного узла; вернуться к шагу 1.

Шаг 6. Если у текущего узла существует правое поддерево, то сделать его корень текущим узлом и перейти к шагу 3; иначе – перейти к шагу 7.

Шаг 7. Создать новый узел; поместить в него очередной идентификатор как значение ключа; в указатель на правое поддерево текущего узла записать адрес вновь созданного узла; вернуться к шагу 1.

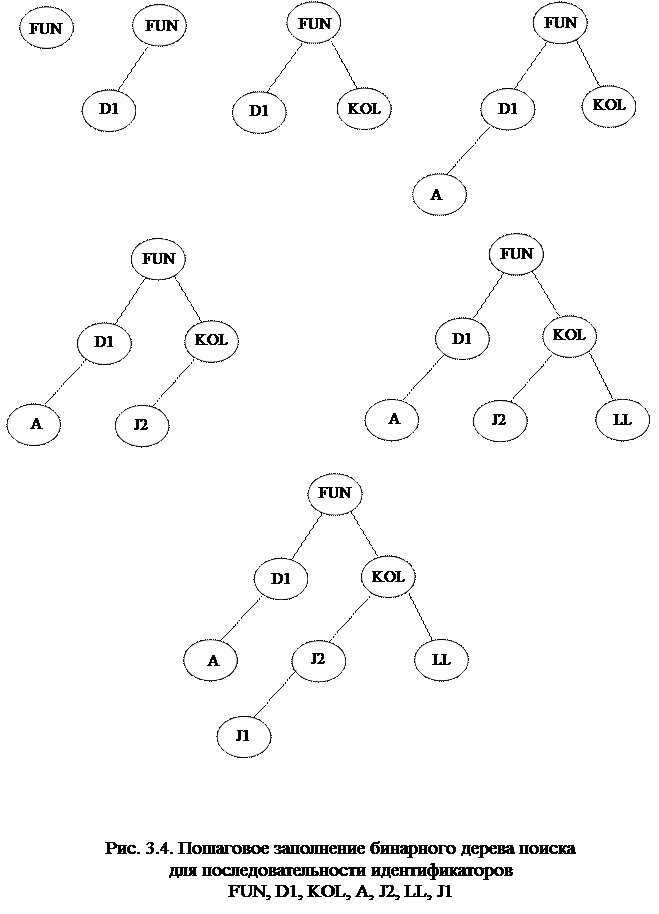
Рассмотрим в качестве примера последовательность идентификаторов FUN, D1, KOL, A, J2, LL, J1. Процесс построения бинарного дерева поиска для

		а) Диаграмма бинарного дерева
		б) Пример отображения бинарного дерева на память
		Рис. 3.3. Представление структуры бинарного дерева в памяти ЭВМ

этой последовательности идентификаторов детально изображается на рис.3.4.

Алгоритм поиска элемента в таблице идентификаторов, построенной по методу бинарного дерева поиска.

Шаг 1. Сделать текущим узлом корень дерева.

Шаг 2. Сравнить аргумент поиска с ключом текущего узла дерева. Если они равны – искомый элемент найден, выполнение алгоритма прекращается; если аргумент поиска меньше значения ключа текущего узла - перейти к шагу 3; иначе – перейти к шагу 4.

Шаг 3. Если у текущего узла существует левое поддерево, то сделать его корень текущим узлом и перейти к шагу 2; иначе – искомый элемент не найден, выполнение алгоритма прекращается.

Шаг 4. Если у текущего узла существует правое поддерево, то сделать его корень текущим узлом и перейти к шагу 2; иначе – искомый элемент не найден, выполнение алгоритма прекращается.

Например, произведем поиск идентификатора J2 в бинарном дереве, изображенном на рис. 3.4. Сначала текущим узлом является корень дерева. Сравниваем идентификаторы J2 и FUN – искомый идентификатор больше, поэтому переходим к рассмотрению правого поддерева текущего узла. Делаем текущим узлом корень этого поддерева и опять сравниваем идентификаторы: J2 меньше KOL, значит дальнейший поиск следует вести в левом поддереве текущего узла. Считаем теперь текущим узлом корень левого поддерева и осуществляем сравнение идентификаторов: J2 равно J2 – идентификатор найден.

Проследим теперь порядок поиска такого идентификатора, который отсутствует в рассматриваемом нами бинарном дереве. Пусть аргументом поиска является идентификатор D2. Начинаем поиск с корневого узла дерева. Поскольку D2 меньше FUN, делаем текущим узел D1 и производим очередное сравнение. Искомый идентификатор больше D1, но так как правое поддерево у текущего узла отсутствует – идентификатор не найден, и выполнение алгоритма прекращается.

Для данного метода число требуемых сравнений и форма бинарного дерева непосредственно зависят порядка поступления идентификаторов. В ряде случаев бинарное дерево вырождается в упорядоченный однонаправленный связный список (например, для последовательности идентификаторов А1, А2, А3, А4, А5). Высота такого бинарного дерева равна количеству идентификаторов n, в силу чего доступ к данным существенно замедляется. Чтобы этого избежать, задачу построения дерева необходимо несколько усложнить, так, чтобы на каждом уровне располагалось максимально возможное количество узлов, а высота дерева, соответственно, была минимальной.

Для решения подобной задачи вводится понятие сбалансированности дерева и выделяется класс сбалансированных деревьев, обладающих всеми преимуществами бинарных деревьев поиска и никогда не вырождающихся. Такие деревья часто называют АВЛ-деревьями по имени их открывателей (Андельсон-Вельский Г.М., Ландис Е.М.). Особенности и порядок построения АВЛ-деревьев подробно описываются в [10].

В общем случае последовательность идентификаторов в исходной программе является статистически неупорядоченной и, соответственно, построенное бинарное дерево является невырожденным. Тогда среднее время Т_з заполнения бинарного дерева из n идентификаторов и среднее время Т_п поиска в нем оценивается следующим образом:

Т_з= О(n*log₂ n),

Т_п= О(log₂ n)

Метод бинарного дерева в целом достаточно эффективен и используется в ряде компиляторов для организации таблиц идентификаторов [14]. Некоторые компиляторы строят несколько различных деревьев для идентификаторов разных типов и разной длины [23, 74].