Пример 1. 7. 1. Аксиома сложения

Студент подготовился к ответу на первые 15 вопросов из 20 вопросов экзамена. Вопрос для ответа на экзамене выбирается наудачу. События: 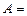{выбран «хороший» билет}, 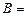{выбран билет из второй половины списка}. Найти вероятност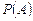и и .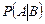

◄По формуле классической вероятности находим: 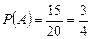, , 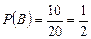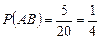. Далее, из (3.1.3) получаем: .

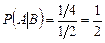Рассмотрим условную вероятность 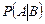как безусловную вероятность, заданную на пространстве элементарных исходов 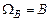. В данном случа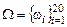е , где 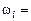{выбран вопрос с 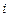-номером},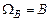 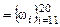. Если рассматривать в качестве пространства элементарных исходов множество 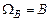, то получим: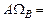 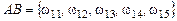. Поэтому .

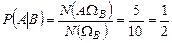Итак, , .►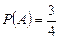

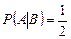Условная вероятность обладает всеми свойствами безусловной вероятности, т.к. для неё выполняются аксиомы обычной вероятности:

1. 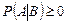(аксиома неотрицательности);

2. 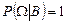(аксиома нормированности);

3. 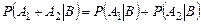, если события 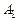и 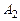несовместны (аксиома сложения).

Упражнения

1.7.1. Убедитесь в выполнении аксиом неотрицательности и нормированности для условной вероятности.

1.7.2. Используя равенство (1.7.3) и свойство дистрибутивности умножения относительно сложения, докажите аксиому сложения для условной вероятности.

Замечания

1. На основании расширенной аксиомы сложения для безусловной вероятности можно убедиться в выполнении аналогичной аксиомы для условной вероятности:

.

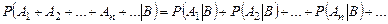2. Из (1.7.3) следует формула умножения вероятностей:

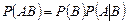. (1.7.4)

3. Поменяв в (1.7.4) местами события и , и полагая 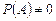, получим:

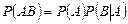. (1.7.5)

Из (1.7.4) и (1.7.5) получаем так называемую теорему умножения

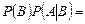
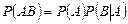: (1.7.6)

вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло.