Выберем за начальное значение x0 тот конец отрезка, для которого знак функции f (x)совпадает со знаком ее второй производной f" (x). Положим для определенности, что f" (x) >0 при a £ x £ b и f (b) >0. Выберем, например, x0=b, для которого f (x0) f" (x0) >0. Проведем касательную к кривой y=f (x)в точке B0 [ x0, f (x0)]. В качестве первого приближения x1 корня x возьмем абсциссу точки пересечения этой касательной с осью Ox (рис. 4.7) и т. д.
Приведем итерационные формулы метода Ньютона:
xn+1= xn- 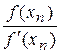 (n=0, 1, 2,…), x0=b.
(n=0, 1, 2,…), x0=b.
Заметим, что если положить x0=a и, следовательно, f (x0) f" (x0) <0, то, проведя касательную к кривой y=f (x)в точке A[ a, f (a)], мы получили бы точку 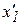 , лежащую вне отрезка[ a, b ] (см. рис. 4.7).
, лежащую вне отрезка[ a, b ] (см. рис. 4.7).
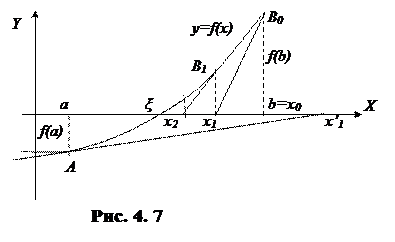 |
Метод имеет квадратичную сходимость, то есть погрешность на (n+1) -й итерации пропорциональна квадрату погрешности на n -й итерации. Метод второго порядка точности.
Для оценки погрешности n -го приближения можно воспользоваться формулой:
| xn-x | £ 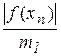 или | xn-x | £
или | xn-x | £ 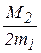 (xn - xn-1) 2,
(xn - xn-1) 2,
где m1 = min | f' (x)|, M2 =max| f" (x)| для всех x 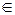 [ a, b ].
[ a, b ].
|
|
|
Если f" (x) не задан, то начальное приближение можно искать по формулам:
с=a - 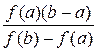
 2015-07-14
2015-07-14 407
407








