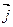
Азн.17.1. f ÎEnd(V). Падпрастора U прасторы V называецца інварыянтнай адносна f (ці f - інварыянтнай), калі 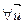 Î U
Î U 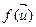 Î U (1)
Î U (1)
Прыклад 17.2.1. V = V2, pr x – праекцыя на вось Ox. U 1 = R 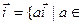 R } - інварыянтная адносна prx падпрастора, так як
R } - інварыянтная адносна prx падпрастора, так як 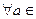 R,
R, 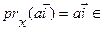 U 1. U 2=R
U 1. U 2=R 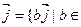 R } - таксама інварыянтныя адносна prx падпрастора, так як
R } - таксама інварыянтныя адносна prx падпрастора, так як 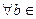 R,
R, 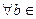 R
R 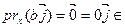 U 2.
U 2. 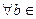 R
R 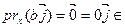 U 2.
U 2.
17.2.2. V = V3, f – паварот вакол восі Oz на вугал 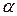 . f -інварыянтнымі з’яўляюцца U z і U xoy - прастора вектароў плоскасці xOy.
. f -інварыянтнымі з’яўляюцца U z і U xoy - прастора вектароў плоскасці xOy.
17.2.3. Для аператара D дыферанцавання прасторы P [x] для адвольага натуральнага n прасторы P n[x] з’яўляецца D -інварыянтнымі.
17.2.4. Для адвольнага f Î End(V) падпрасторы 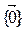 і V з’яўляюцца f - інварыянтнымі.. Яны называюца трывіяльнымі.
і V з’яўляюцца f - інварыянтнымі.. Яны называюца трывіяльнымі.
Ул-ць 17.3 Калі f ÎEnd(V), U 1 і U 2 f - інварыянтныя падпрасторы, тады U 1 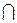 U 2 таксама f - інварыянтная падпрастора.
U 2 таксама f - інварыянтная падпрастора.
Доказ. Разгледзім 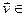 U 1
U 1 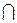 U 2 . Тады
U 2 . Тады 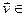 U 1 адкуль вынікае, што
U 1 адкуль вынікае, што 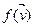 Î U 1. Аналагічна,
Î U 1. Аналагічна, 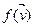 Î U 2, што і трэба было даказаць.■
Î U 2, што і трэба было даказаць.■
Азн. 17.4. Ненулявы вектар 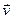 Î V называецца ўласным вектарам аператара f ÎEnd(V), калі існуе
Î V называецца ўласным вектарам аператара f ÎEnd(V), калі існуе 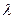 ÎP такі, што f
ÎP такі, што f 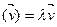 . Пры гэтым кажуць, што
. Пры гэтым кажуць, што 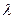 - уласнаезначэнне лінейнага аператара f, якое адпавядае вектару
- уласнаезначэнне лінейнага аператара f, якое адпавядае вектару 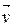 .
.
|
|
|
 2015-07-14
2015-07-14 234
234







